Определение расхода газа, истекающего через сходящуюся насадку
Лекция 8.
Определение расхода газа, истекающего через сходящуюся насадку.
Рассмотрим истечение газа из резервуара, где параметры газа  и
и  , через сужающееся сопло в полость, давление в которой
, через сужающееся сопло в полость, давление в которой  .
.

Рассмотрим установившийся режим течения. Газ в дальнейшем будем считать идеальным. Будем так же полагать, что скорость газа резервуаре пренебрежимо мала, т.е.  ,
,  и
и  - параметры торможения.
- параметры торможения.
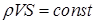
Полагая, что поток теплоизолирован, трение отсутствует:
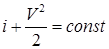
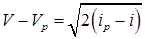
Рекомендуемые материалы
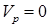
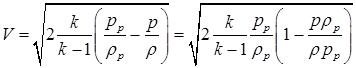
т.к. поток энергоизолирован, изменение  и
и  потоке происходит в соответствии с уравнением адиабаты:
потоке происходит в соответствии с уравнением адиабаты:
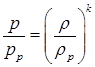
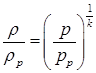
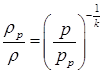
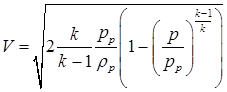
Для любого сечения 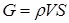
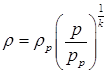
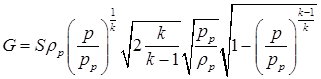
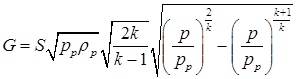
Если в выходном сечении давление  , т.е. давление в полости, куда происходит истечение, то:
, т.е. давление в полости, куда происходит истечение, то:
 (1.52)
(1.52)
Зависимость (1.52) называется формулой Сен-Венана и Веитцеля.
Проведем исследование (1.52). Обозначим  через
через  и построим для некоторого сечения зависимость
и построим для некоторого сечения зависимость  .
.
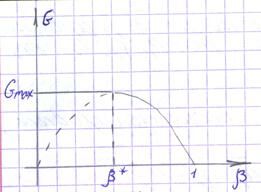
При уменьшении  от 1 до
от 1 до  расход G увеличивается от 0 до Gmax. Исследуем параметры режима, в котором расход достигает максимума:
расход G увеличивается от 0 до Gmax. Исследуем параметры режима, в котором расход достигает максимума:
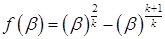
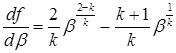
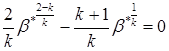
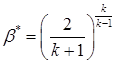
В данном режиме:
 (1.53)
(1.53)
Обратившись к зависимости (1.45) убедимся, что данный режим является критическим, т.е. скорость газа в выходном сечении в этом режиме равна местной скорости звука.

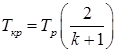
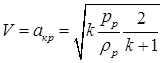
 (1.54)
(1.54)
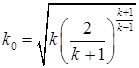
 (1.54.а)
(1.54.а)
Если уменьшить  до значения меньше
до значения меньше  , то согласно (1.52), расход должен уменьшиться. Опыт показывает, что в этом случае расход остается неизменным, сохраняя значение
, то согласно (1.52), расход должен уменьшиться. Опыт показывает, что в этом случае расход остается неизменным, сохраняя значение  , что соответствует горизонтальному участку графика
, что соответствует горизонтальному участку графика  . При этом в выходном сечении сохраняются параметры критического режима:
. При этом в выходном сечении сохраняются параметры критического режима:  ,
,  ,
,  ,
,  .
.
Физический смысл этого явления состоит в том, что если, скорость течения в выходном сечении равна местной скорости звука, то давление  , которое может поникнуть в выходное сечение.
, которое может поникнуть в выходное сечение.
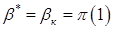
При отношении давлений  режим течения в выходном сечении критический. Его значение определяется функциями: (1.54), (1.54.а).
режим течения в выходном сечении критический. Его значение определяется функциями: (1.54), (1.54.а).
Если  , то скорость в выходном сечении меньше скорости звука. Будем называть этот режим докритическим. В этом режиме давление в выходном сечении равно давлению в полости, куда истекает газ. Величина расхода определяется формулой (1.52).
, то скорость в выходном сечении меньше скорости звука. Будем называть этот режим докритическим. В этом режиме давление в выходном сечении равно давлению в полости, куда истекает газ. Величина расхода определяется формулой (1.52).
Если  , то полученные формулы теряют смысл.
, то полученные формулы теряют смысл.
Объединим (1.52) и (1.54) в единую запись:
 (1.55)
(1.55)
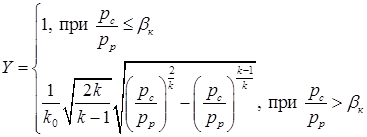
Т.к. (1.55) теряет смысл при  , то еще доопределяют, что
, то еще доопределяют, что  , при
, при  .
.
Физический смысл  - отношение текущего значения расхода к максимальному (критическому).
- отношение текущего значения расхода к максимальному (критическому).
38. Классификация эл. установок и помещений по электробезопасности - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
Зависимость (1.55) широко используется в инженерной практике для определения расхода в дросселирующих устройствах. Простейшее из них дроссельная шайба:
Более сложные устройства изменяют площадь прохождения газа. Это газораспределители силовых пневмоприводов, клапанные пары и др. Условия протекания газа через эти устройства заметно отличаются от тех условий, которые служили для выведения формулы (1.55). В связи с разрывами потока при течении возможно образование мертвых зон, поток может подтормаживаться. Распределение скорости в дросселе может быть неравномерным.
Если рассчитывать величину расхода по зависимости (1.55), полагая, что Sвых – это площадь дросселирующего сечения, то полученное значение расхода будет несколько больше фактического. Для компенсации этого несоответствия в формулу (1.55) вводят поправочный коэффициент  .
.
 (1.55.а)
(1.55.а)
Для определенного типа дроссельных устройств величина  лежитв узких пределах. Его обычно определяют экспериментом.
лежитв узких пределах. Его обычно определяют экспериментом.




















