Последовательность проточных полостей

Лекция 22.

Последовательность проточных полостей.

Рассмотрим задачу определения параметров статического режима в последовательности проточных полостей, считая, что параметры газа в источнике  и  постоянны.

Система дифференциальных уравнений, определяющих значения переменных как в установившемся, так и в переходном процессах, строится аналогично тому, как показано в предыдущем примере.

Также аналогично предыдущему, получаются зависимости, определяющие переменные в стационарном режиме.

Приведем уравнение для установившегося режима.

,                                     

                               

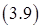
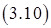
Рекомендуемые материалы

.

Решаем систему (3.10) и легко находим, что заведомо известно, что режим течения из -ой полости в атмосферу критический, т.е., если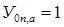

.

Если , то ,  и .

Если , то  вычисляется по формуле (3.8а).

Далее находим .

По второй формуле системы (3.10) вычисляем  и .

Продолжая расчет, найдем отношение всех давлений, а затем при известном  находим установившиеся значения давлений во всех полостях.

Задача.

Сжатый воздух запасен в ресивере, имеющем постоянное давление  и , протекая через три проточные полости, истекает в атмосферу. Известны значения эффективных площадей  всех дросселей.

Найти значение давления , при котором массовый секундный расход воздуха из ресивера будет равен заданному.

Воздух – идеальный газ, теплообменом пренебрегаем.

,

,

,

.

.

Предположим, что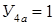

, ,

 (при ),

,

,

.

Это подтверждает, что течение в атмосферу критическое .

Находим отношение давлений

, ,

, ,

,

, ,

Вместе с этой лекцией читают "3. Создание информационных систем, качество и эффективность ".

,

,

, ,

,

,

.