Математическая модель процессов проточной полости сложной конфигурации

Лекция 14.

Математическая модель процессов проточной полости сложной конфигурации.

При построении модели процесса в полости полагают, что во всех точках ее объема параметры рабочего тела одинаковы. При малых размерах полости давление по объему выравнивается весьма быстро, но такое же быстрое выравнивание температуры происходит лишь тогда, когда имеет место быстрое и интенсивное вынужденное перемешивание рабочего тела внутри полости.

В рабочих полостях сложной конфигурации такого перемешивания может и не быть.

Существуют конструкции, в которых допущения мгновенного выравнивания вполне оправданы, но в то же время температура в различных элементах полости может существенно различаться.

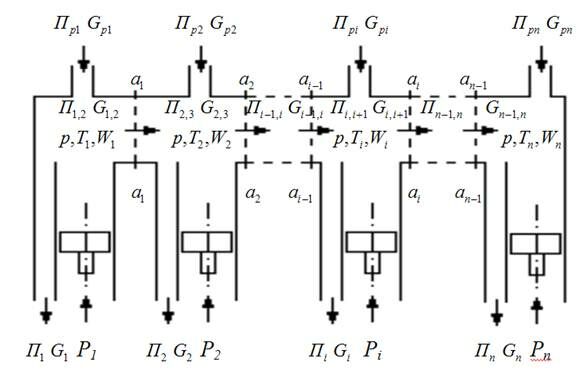
На рисунке представлена схема полости, включающая  элементов (силовых цилиндров), соединенных между собой широкими короткими каналами.

В любой момент времени давление  во всех элементах полости практически одинаково, но, т.к. интенсивный массобмен между цилиндрами отсутствует, то  различны. В то же время температура внутри каждого из объемов в любой точке может считаться одинаковой.

Будем считать, что обратное течение газа по подводящим и отводящим каналам невозможно.

Рекомендуемые материалы

Состав рабочего тела, поступающего из различных источников, постоянен и не изменяется. Рабочим телом является идеальный газ.

На основе закона сохранения энергии для газа во всем объеме полости запишем уравнение

.                      

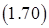
На основе закона сохранения массы для каждого элемента полости запишем уравнение

.                            

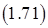
Входящие в зависимости (1.70) и (1.71) величины перетечек могут быть найдены из условия мгновенного выравнивания давления в элементах полости. Для этого запишем на основе закона сохранения энергии уравнение для давления, приняв при этом во внимание, что давление в этом элементе одно и тоже

,       

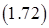
где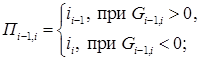

Информация в лекции "2 Сословная и классовая структура российского общества" поможет Вам.

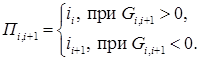
Приравниваем правые части зависимостей (1.70) и (1.72) и полученное уравнение разрешаем относительно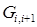

.                                  

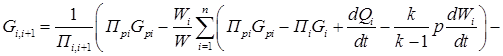
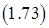
Для первого элемента величина  и по зависимости (1.73) легко рассчитать величину , а затем последовательно значения всех расходов перетечек. Направление перетечек определяется знаком выражения во внешних скобках формулы (1.73), а потому неоднозначность выражения для  легко преодолевается. При детализации уравнений величина утечки

.