Динамическое программирование
6.Лекция. Динамическое программирование.
6.1. Постановка задачи.
Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги).
Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.
Экономический процесс является управляемым, если можно влиять на ход его развития.
Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.
Рекомендуемые материалы
Операция – управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.
Решение на каждом шаге называется «шаговым управлением».
Совокупность всех шаговых управлений представляет собой управление операцией в целом.
При распределении средств между предприятиями шагами целесообразно считать номер очередного предприятия; при распределении на несколько лет ресурсов деятельности предприятия – временной период. В других задачах разделение на шаги вводится искусственно.
Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:
F(x)= 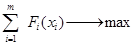
Где F – выигрыш за операцию;
Fi(xi) – выигрыш на i-м шаге;
х – управление операцией в целом;
хi – управление на i-м шаге (i=1,2,…,m). В общем случае шаговые управления (х1, х2, … хm) могут стать числами, векторами, функциями.
То управление (х*), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управлений х* = х*1, х*2, … х*m
F* = max {F*(х*)} – максимальный выигрыш, который достигается при оптимальном управлении х*.
Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.
6.2. Принцип оптимальности Беллмана.
Основным методом динамического программирования является метод рекуррентных соотношений; который основывается на использовании принципа оптимальности, разработанного американским математиком Р.Беллманом.
Суть принципа:
Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться ОПТИМАЛЬНЫМИ относительно состояния, к которому придет система в конце каждого шага.
Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
 Условная оптимизация
Условная оптимизация
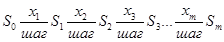
Безусловная оптимизация
 Si – состояние системы на i-м шаге. Основная рекуррентная формула динамического программирования в случае решения задачи максимизации имеет вид:
Si – состояние системы на i-м шаге. Основная рекуррентная формула динамического программирования в случае решения задачи максимизации имеет вид:
 , где максимум в данной формуле берется по всем возможным решениям в ситуации, когда система на шаге m находится в состоянии i.
, где максимум в данной формуле берется по всем возможным решениям в ситуации, когда система на шаге m находится в состоянии i.
Величина fm(i) – есть максимальная прибыль завершения задачи из состояния i, если предположить, что на шаге m, система находится в состоянии i.
Максимальная прибыль может быть получена максимизацией суммы прибылей самого шага m и максимальной прибыли шага (m+1) и далее, чтобы дойти до конца задачи.
Планируя многошаговую операцию надо выбирать управление на каждом шаге с учетом всех его будущих последствий на ещё предстоящих шагах.
Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимальным, а так, чтобы была максимальна сумма выигрышей на всех оставшихся шагах плюс данный шаг.
Среди всех шагов последний шаг планируется без оглядки на будущее, т.е. чтобы он сам, как таковой принес наибольшую выгоду.
Задача динамического программирования начинает решаться с конца, т.е. с последнего шага. Решается задача в 2 этапа:
1 этап (от конца к началу по шагам): Проводится условная оптимизация, в результате чего находится условные оптимальные управления и условные оптимальные выигрыши по всем шагам процесса.
2 этап (от начала к концу по шагам): Выбираются (прочитываются) уже готовые рекомендации от 1-го шага до последнего и находится безусловное оптимальное управление х*, равный х*1, х*2, …, х*m.
6.3. Задача распределения средств на 1 год.
Пример: имеется запас средств, который нужно распределить между предприятиями, чтобы получить наибольшую прибыль. Пусть начальный капитал S0=100 д.ед. Функции дохода предприятий даны в матрице прибылей по каждому предприятию.
| Х | 1 предприятие f (х1) | 2 предприятие f (х2) | 3 предприятие f (х3) | 4 предприятие f (х4) |
| 20 | 3 | 2 | 3 | 3 |
| 40 | 4 | 5 | 4 | 6 |
| 60 | 9 | 8 | 9 | 8 |
| 80 | 11 | 7 | 5 | 7 |
| 100 | 12 | 15 | 12 | 14 |
Решение:
Схема решения:
 4 предприятия Условная оптимизация
4 предприятия Условная оптимизация
денег всего S0=80
 So____Iпр____S1____IIпр_____S2____IIIпр____S3____IVпр________S4
So____Iпр____S1____IIпр_____S2____IIIпр____S3____IVпр________S4



 1шаг 2 шаг 3 шаг 4 шаг
1шаг 2 шаг 3 шаг 4 шаг
х1 х2 х3 х4
f(x1) f(x2) f(x3) f(x4)
F4=max{f(x4)}
 |
Безусловная F3=max{ f(x3)+F4}


Оптимизация F2=max{ f(x2)+F3}

F1=max{ f(x1)+F2}
 Используется принцип Беллмана:
Используется принцип Беллмана:
Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце каждого шага. Использование данного принципа гарантирует, что управление , выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
математическая модель прямой задачи:
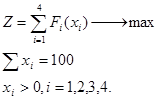
Экономический смысл переменных:
xi – количество денег, вкладываемых в i предприятие.
Si – количество денег, оставшихся после вложения в i-предприятие (состояние системы на i-шаге);
F(xi) – прибыль от вложенной суммы денег;
S0 – начальный капитал.
Рассмотрим 4-й шаг:
На 4-ом предприятии может остаться либо 0, либо 20, либо 40, либо 60, либо 100 д.ед.Тогда прибыль от вложения денег можно получить следующую.
| S3 | Х4 | f (x4) | F4 |
| 0 | 0 | 0 | 0 |
| 20 | 20 | 3 | 3 |
| 40 | 40 | 6 | 6 |
| 60 | 60 | 8 | 8 |
| 80 | 80 | 7 | 7 |
| 100 | 100 | 14 | 14 |
Рассмотрим 3-й шаг:
На 3-ем и 4-ем предприятии может остаться либо 0, либо 20, либо 40, либо 60, либо 100 д.ед. Рассмотрим первую возможность. Если 3-му предприятию мы выдаем 20 д.ед. то 4-му предприятию ничего не остается, и наоборот. Соответственно 40 д.ед.можно поделить так (0;40), (20;20);
60 д.ед. – (0;60), (20;40), (40;20), (60;0).
Прибыль от вложения денег в 3-е предприятие берется в исходной матрице прибылей, а прибыль от вложений, денег в 4-е предприятие берется из таблицы предыдущего шага
Прибыль на 3-м шаге берется максимальной по каждому вложению.
| Вклад | Проект | Остаток | Прибыль из матрицы | Прибыль за шаг | Прибыль на шаге | |
| S2 | Х3 | S3 | f (x3) | F4 | f+F | F3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 20 | 0 | 3 | 3 | 3 |
| 20 | 0 | 3 | 0 | 3 | ||
| 40 | 0 | 40 | 0 | 6 | 6 | 6 |
| 20 | 20 | 3 | 3 | 6 | ||
| 40 | 0 | 4 | 0 | 4 | ||
| 60 | 0 | 60 | 0 | 8 | 8 | 9 |
| 20 | 40 | 3 | 6 | 9 | ||
| 40 | 20 | 4 | 3 | 7 | ||
| 60 | 0 | 9 | 0 | 9 | ||
| 80 | 0 | 80 | 0 | 7 | 7 | 12 |
| 20 | 60 | 3 | 8 | 11 | ||
| 40 | 40 | 4 | 6 | 10 | ||
| 60 | 20 | 9 | 3 | 12 | ||
| 80 | 0 | 5 | 0 | 5 | ||
| 100 | 0 | 100 | 0 | 14 | 14 | 15 |
| 20 | 80 | 3 | 7 | 10 | ||
| 40 | 60 | 4 | 8 | 12 | ||
| 60 | 40 | 9 | 6 | 15 | ||
| 80 | 20 | 5 | 3 | 8 | ||
| 100 | 0 | 12 | 0 | 12 |
Рассмотрим 2-й шаг.
| Вклад | Проект | Остаток | Прибыль из матрицы | Прибыль за шаг | Прибыль на шаге | |
| S1 | Х2 | S2 | f (x2) | F3 | f+F | F2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 20 | 0 | 3 | 3 | 3 |
| 20 | 0 | 2 | 0 | 2 | ||
| 40 | 0 | 40 | 0 | 6 | 6 | 6 |
| 20 | 20 | 2 | 3 | 5 | ||
| 40 | 0 | 5 | 0 | 5 | ||
| 60 | 0 | 60 | 0 | 9 | 9 | 9 |
| 20 | 40 | 2 | 6 | 8 | ||
| 40 | 20 | 5 | 3 | 8 | ||
| 60 | 0 | 8 | 0 | 8 | ||
| 80 | 0 | 80 | 0 | 12 | 12 | 12 |
| 20 | 60 | 2 | 9 | 11 | ||
| 40 | 40 | 5 | 6 | 11 | ||
| 60 | 20 | 8 | 3 | 11 | ||
| 80 | 0 | 7 | 0 | 7 | ||
| 100 | 0 | 100 | 0 | 15 | 15 | 15 |
| 20 | 80 | 2 | 12 | 14 | ||
| 40 | 60 | 5 | 9 | 14 | ||
| 60 | 40 | 8 | 6 | 14 | ||
| 80 | 20 | 7 | 3 | 10 | ||
| 100 | 0 | 15 | 0 | 15 |
Рассмотрим 1-й шаг.
| Вклад | Проект | Остаток | Прибыль из матрицы | Прибыль за шаг | Прибыль на шаге | |
| S1 | Х2 | S2 | f (x2) | F3 | f+F | F2 |
| 100 | 0 | 100 | 0 | 15 | 15 | 15 |
| 20 | 80 | 3 | 12 | 15 | ||
| 40 | 60 | 4 | 9 | 13 | ||
| 60 | 40 | 9 | 6 | 15 | ||
| 80 | 20 | 11 | 3 | 14 | ||
| 100 | 0 | 12 | 0 | 12 |
Анализ результатов:
Максимальная прибыль равна 15 д.ед. Расположить денежные средства между проектами можно несколькими способами:
1)1 проект – 0 д.ед., 2 проект – 0 д.ед., 3 проект – 60 д.ед., 4 проект – 40 д.ед.
2)1 проект – 0 д.ед., 2 проект – 100 д.ед., 3 проект – 0 д.ед., 4 проект – 0 д.ед.
3)1 проект – 20 д.ед., 2 проект – 0 д.ед., 3 проект – 60 д.ед., 4 проект – 20 д.ед.
4)1 проект – 60 д.ед., 2 проект – 0 д.ед., 3 проект – 20 д.ед., 4 проект – 20 д.ед.
5)1 проект – 60 д.ед., 2 проект – 0 д.ед., 3 проект – 0 д.ед., 4 проект – 40 д.ед.
6.4. Задача распределения средств на два года
Найти оптимальный способ распределения средств S0 = 100 тыс.руб между двумя предприятиями на два года, если вложенные средства в первое предприятие дают доход f1(x) = 0.9x и возвращаются в размере j1(x) = 0.5x. Аналогично, для второго предприятия f2(x) = 0.8x и j2(x) = 0.7x.
| 1 предприятие | 2 предприятие | Всего | |
| Средства в начале года 1 года | х1 | 100-х1 | 100 |
| Прибыль на первом году | 0,9х1 | 0,8(100-х1) | (0,9-0,8)х1+80 |
| Возврат денег | 0,5х1 | 0,7(100-х1) | (0,5-0,7)х1+70 =70-0,2х1 |
| Средства в начале 2 года | х2 | 70-0,2х1- х2 | 70-0,2х1 |
| Прибыль во втором году | 0,9х2 | Ещё посмотрите лекцию "5.23 Балканские войны" по этой теме. 0,8(70-0,2х1- х2) | 56-0,16х1+0,1х2 |
| Прибыль за два года | 0,1х1+80+56-0,16х1+0,1х2=136-0,6х1+0,1х2 |
Отсюда можно сделать вывод о том, что х1=0, х2=70, максимальная прибыль за два года составит 143 ден. ед.

















