Погрешность квадратурных формул. Правило Рунге

Погрешность квадратурных формул. Правило Рунге.

Пусть квадратурная формула  точна для многочленов степени m (n ≤ m). Для оценки погрешности воспользуемся разложением f(x) по формуле Тейлора:

.

Тогда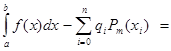

.

Т.е.  — погрешность квадратурной формулы.

Пример.

1) Для простейших формул прямоугольников и трапеций

Рекомендуемые материалы

.

2) Для формулы Симпсона

.

Теперь воспользуемся разложением  f(x)  по формуле Тейлора степени (m+1):

/

Тогда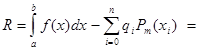

.

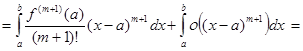
Опр. Главным членом погрешности называется .

Правило Рунге — способ оценки главного члена погрешности без использования производной (m + 1) порядка.

Пусть I_h — приближенное значение интеграла , вычисленное по составной квадратурной формуле с длиной участка .

Тогда .

.

В лекции "53 Новая фаза гуситского движения" также много полезной информации.