Метод прогонки

Метод прогонки.

Запишем систему (45) в канонической форме:

,

, .

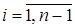
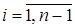Получим:

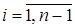, .                                    (46)

Будем искать  в виде:

.                                                (47)

где коэффициенты  требуется определить. Выразим  и подставим в исходную систему (46):

Рекомендуемые материалы

.

Выразим из последнего выражения :

.

Сравнивая полученную формулу с (47), получим выражения для :

                                     (48)

Чтобы начать расчеты по этим формулам, надо знать . Найдем их из первого краевого условия. Выражая  и сравнивая с , получим ; .

Итак, вычисления, называемые прямым ходом, осуществляют в следующем порядке:

1. Вычисляют значения .

2. Находят .

3. Вычисляют , .

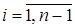Обратный ход вычислений состоит в следующем:

1. Решают систему из двух уравнений относительно  и :

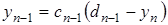
"ДЮРКГЕЙМ Эмиль" - тут тоже много полезного для Вас.

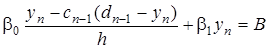
и получают .

2. Вычисляют , начиная с  и далее до .

3. Находят .

В результате работы алгоритма получим значения  исходной функции в узловых точках , т.е. получим таблицу значений функций, которая является приближенным решением исходной задачи. Используя полученную таблицу, можно построить аналитический вид функции. Как правило, эту функцию строят в виде многочлена.

Для оценки погрешности метода конечных разностей применяют двойной пересчет с шагом  и . Приближенная оценка погрешности значения получается по формуле , где  - значение точного решения краевой задачи в точке :  и  - значения в точке , полученные соответственно с шагом  и .