Задачи, приводящие к дифференциальным уравнениям

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, f'(x)=f(f(x)) не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функцияy(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,y⁽ⁿ⁾(x) до порядка nвключительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

$Fleft(x,y,y',y'',...,y^{(n)}right)=0!$ или $Fleft(x,y,frac{dy}{dx},frac{d^{2}y}{dx^2},...,frac{d^{n}y}{dx^n}right)=0$ ,

где ~y=y(x) — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной , штрих означает дифференцирование по . Число называется порядком дифференциального уравнения.

Дифференциальные уравнения в частных производных

Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:

$F left(x_1, x_2,dots, x_m, z, frac{partial z}{partial x_1}, frac{partial z}{partial x_2},dots, frac{partial z}{partial x_m}, frac{partial^2 z}{partial x_1^2}, frac{partial^2 z}{partial x_1 partial x_2}, frac{partial^2 z}{partial x_2^2},dots,frac{partial^n z}{partial x_m^n}right)= 0$ ,

где x_1, x_2,dots, x_m — независимые переменные, а z! = z(x_1, x_2,dots, x_m) — функция этих переменных.

Примеры

y'' + 9y = 0 — однородное дифференциальное уравнение второго порядка. Решением является семейство функций y = (C₁cos(3x) + C₂sin(3x)), где C₁ и C₂ — произвольные константы.

Второй закон Ньютона можно записать в форме дифференциального уравнения $m frac{d^2 x}{dt^2}= F(x,t)$ , где m — масса тела, x — его координата, F(x,t) — сила, действующее на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

Колебание струны задается уравнением $frac{partial{}^2 u}{partial t^2}=a^2 frac{partial^2 u}{partial x^2}$ , где u = u(x,t) — отклонение струны в точке с координатой x в момент времени t, параметр a задает свойства струны. Это так называемое волновое уравнение.

Частное решение дифференциального уравнения

Частным решением дифференциального уравнения на интервале (alpha;;beta) называется каждая функция y(x), которая при подстановке в уравнение вида

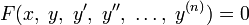
$F(x,;y,;y',;y'',;ldots,;y^{(n)})=0$

обращает его в верное тождество на интервале (alpha;;beta) .

Зная общее решениеоднородного дифференциального уравнения и любое частное решение неоднородного уравнения, можно получить общее решение неоднородного уравнения в виде суммы общего решения однородного уравнения и частного решения неоднородного.

Общее решение дифференциального уравнения

[

Общее решение дифференциального уравнения — функция наиболее общего вида, которая при подстановке в дифференциальное уравнение вида

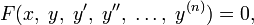
$F(x,;y,;y',;y'',;ldots,;y^{(n)})=0,$

обращает его в тождество.

Если каждое решение дифференциального уравнения представимо в виде:

$y=varphi(x,;C_{1}^{0},;C_{2}^{0},;ldots,;C_{n}^{0}),$

где $C_{1}^{0},;;C_{2}^{0},;;ldots,;;C_{n}^{0}$ — конкретные числа, то функция вида

$y=varphi(x,;C_{1},;C_{2},;ldots,;C_{n})$

при всех допустимых значениях параметров (неопределённых констант) $C_{1},;;C_{2},;;ldots,;;C_{n}$ называется общим решением дифференциального уравнения.

Пусть y(x) — некоторая функция, y'(x) — ее производная. Для удобства будем записывать производную виде $frac {dy} {dx} = y'(x)$ , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал dx — приращение значения переменной в окрестности x, стремящееся к нулю. Дифференциал функции dy — малое приращение функции, dy = f(x + dx) − f(x) = y'(x)dx. Пусть f(x) и g(y) — некоторые функции от x и y. Рассмотрим уравнение

$frac {dy} {dx} = f(x) g(y)$ .

Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на $frac {dx} {g(y)}$ :

$frac {dy} {g(y)} = f(x) dx$ .

Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при x = x₀y = y₀ и возьмем интегралы от левой и правой частей. Пределы интегрирования — от y₀ до y для левой части и от x₀ для x для правой части уравнения:

$intlimits_{y_0}^{y}frac {dy} {g(y)} = intlimits_{x_0}^{x}f(x) dx$ .

Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить y(x).

Значения x₀ и y₀ называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных — int f(x) dx = F(x) + C , где F(x) — первообразная f(x), C — произвольная постоянная, запишем это в виде

$int frac {dy} {g(y)} = int f(x) dx$ .

Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные y, удовлетворяющие уравнению g(y) = 0. При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).

Пример 1

Решить дифференциальное уравнение $frac {dy} {dx} = left (x + 1right ) cos^2 y$ .

Разделим переменные:

$frac {dy} {(cos^2 y)} = left (x + 1 right ) dx$ .

Т. к. начальные условия не заданы, возьмем неопределенный интеграл от обеих частей уравнения:

$int frac {dy} {left (cos^2 yright )} = int left (x + 1 right ) dx$ ,

$operatorname{tg} y = frac {x^2} 2 + x + C$ .

Осталось лишь выразить y через x:

$y = operatorname{arctg} left (frac {x^2} 2 + x + C right )$ .

Найдем также нулевые решения:

$cos^2 y = 0 Leftrightarrow y = frac {pi} 2 + pi n, n in mathbb Z$ .

Ответ: $y(x) = operatorname{arctg} left (frac {x^2} 2 + x + C right ), C = operatorname{const}, y(x) = frac {pi} 2 + pi n, n in mathbb Z$ .

Пример 2

Определить максимальную скорость, которую может развить ракета в космосе. Начальная скорость ракеты равна нулю. Масса ракеты без топлива равна m, с топливом — m₀. Скорость выброса топлива относительно ракеты равна u. Ракета движется вдали от звезд и планет.

Рис. 1

Пусть ракета движется вдоль оси Ox (Рис. 1). В некоторый момент от нее отделяется малая масса топлива ( − dm). При этом скорость ракеты увеличивается на dv. Запишем закон сохранения импульса в проекции на Ox:

mv = ( − dm)(v − u) + (v + dv)(m + dm).

Раскрыв скобки и приведя подобные, получим:

mdv = − udm − dvdm.

Величина dvdm — произведение двух бесконечно малых величин. Поэтому ею можно пренебречь:

mdv = − udm.

Интегрируем:

$intlimits_0^v frac {1} {u} dv = intlimits_{m_0}^m - frac {1} {m} dm$ ,

$left . frac {v} {u} right |_0^v = left . -u ln m right |_{m_0}^{m}$ ,

$frac{v} {u} = - ln m + ln m_0$ ,

$v = u ln frac {m_0} {m}$ .

Впервые эта формула была получена К. Э. Циолковским.

Ответ: $v = u ln frac {m_0} {m}$ .

Пружина жесткостью k с прикрепленным к ней грузом массой m находятся в горизонтальной плоскости в положении равновесия, совпадающем с началом координат. Свободный конец пружины закреплен. Пружина параллельна оси Ox. В начальный момент времени грузу сообщают скорость v₀ вдоль Ox. Найти зависимость координаты груза от времени.

Рис. 2

В произвольный момент времени координата груза равна x, скорость — v (Рис. 2). Запишем закон сохранения энергии:

$frac {mv^2} 2 + frac {kx^2} 2 = frac {mv_0^2} 2$ .

Выполним следующие преобразования:

mv^2 = mv_0^2 - kx^2 ,

$v^2 = v_0^2 - frac k m x^2$ ,

$v = v_0 sqrt {1 - frac k m frac {x^2} {v_0^2}}$ .

Введя обозначение $omega^2= frac k m$ и записав скорость в виде $v = frac {dx} {dt}$ , получим дифференциальное уравнения с разделяющимися переменными:

$frac {dx} {dt} = v_0 sqrt {1 - left (frac {omega x} {v_0} right )^2}$ .

Разделим переменные:

Для этого выполним замену $frac {omega x} {v_0} = sin z$ . Тогда $sqrt {1 - left (frac {omega x} {v_0} right )^2} = sqrt {1 - sin^2 z} = cos z$ . Выразим дифференциал dx: $x = frac {v_0} {omega} sin z$ , $dx = frac {dx} {dz} dz = left (frac {v_0} {omega} sin z right )' dz = frac {v_0} {omega} cos z dz$ . Теперь интегрируем:

"2.3 Кривые Безье" - тут тоже много полезного для Вас.

. Подставляя в уравнение, имеем:

$left . frac {v_0} {omega} arcsin frac{omega x} {v_0} right | _0 ^x = left . v_0 t right | _0 ^t$ ,

$arcsin frac{omega x} {v_0} = omega t$ ,

$x = frac {v_0} {omega} sin omega t$ .

Движения, происходящие по закону синуса или косинуса называются гармоническими колебаниями. Рассмотренная система называется пружинным маятником. Видно, что в нашем случае максимальный модуль координаты равен $frac {v_0} {omega}$ . Он часто обозначается буковой A и называется амплитудой колебаний. Амплитуда гармонических колебаний всегда определяется начальными условиями.

Ответ: $x = A sin omega t, A = frac {v_0} {omega}, omega = sqrt frac k m$

Поделитесь ссылкой:

Популярные услуги

Задачи, приводящие к дифференциальным уравнениям

Рекомендуемые материалы

Рекомендуемые лекции