Вещественное евклидово пространство

Вещественное евклидово пространство                                 

Определение 1.5   Вещественное линейное пространство  называется вещественным евклидовым пространством, если в нем определена операция скалярного умножения векторов, сопоставляющая любой паре векторов  вещественное число, называемое скалярным произведением  на  и обозначаемое, так, что выполняются следующие тождества:

1)  

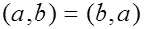
      (коммутативность скалярного умножения);

2)  

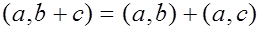
      (дистрибутивность скалярного умножения относительно сложения векторов);

3)   (для любого вещественного );

4)  , причем равенство имеет место тогда и только тогда, когда .

В дальнейшем мы будем рассматривать только вещественное евклидово пространство, называя его просто евклидовым пространством.

Рекомендуемые материалы

Докажем некоторые следствия из определения евклидова пространства.

1)  

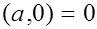
      Действительно, .

2)  

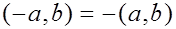
       Имеем: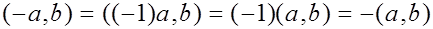

3)  Неравенство Коши-Буняковского:

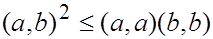
Вычислим для произвольного вещественного  следующее произведение:

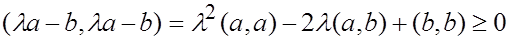
Рассматривая последнее выражение как утверждение о неотрицательности квадратного трехчлена от , получим, что дискриминант неположителен:

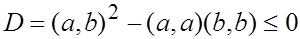
В евклидовом пространстве введем понятие нормы вектора , обозначаемой . По определению

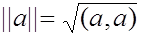
С использованием нормы неравенство Коши-Буняковского перепишется так:

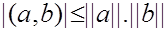
Норма вектора обладает также следующими свойствами:

1)  , причем равенство имеет место только для нулевого вектора.

2)  

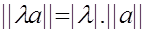
3)   (неравенство треугольника)

Последнее неравенство представляет собой аналог (и обобщение) известного из школьной геометрии свойства сторон треугольника, поскольку - как нетрудно понять - норма геометрического вектора - это его длина.

С помощью нормы мы можем ввести понятие расстояния между векторами евклидова пространства: по определению

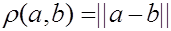
Легко могут быть доказаны следующие свойства расстояния:

1)  , причем равенство имеет место тогда и только тогда, когда ;

2)  

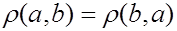
3)  для любых трех векторов  

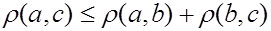
(это неравенство также называется неравенством треугольника).

Примеры. 1) В пространстве  геометрических векторов скалярное умножение вводится обычным образом:

, где- угол между векторами и .

Все свойства (1)-(4) легко проверяются.

2)  В арифметическом векторном пространстве  скалярное произведение векторов  и вводится формулой:

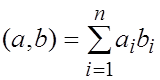
Доказательство свойств предоставляется читателю.

3)  В пространстве  функций, непрерывных на отрезке, определим скалярное произведение векторов (функций) следующим образом:

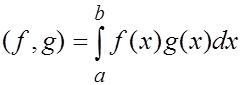
Все свойства скалярного произведения в данном случае легко получаются из известных свойств определенного интеграла. В частности, последнее свойство (неотрицательность скалярного произведения вектора на себя) следует из того, что интеграл от неотрицательной функции неотрицателен).

Интересны в этом пространстве выражение для нормы и вид неравенства Коши-Буняковского:

Обратите внимание на лекцию "Категории помещений и зданий".

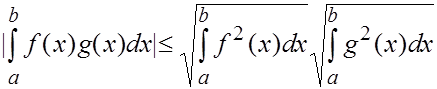
Последнее неравенство часто используется для оценки определенных интегралов.

Расстояние между функциями в  вычисляется как корень квадратный от интеграла от квадрата разности функций:

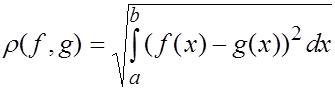
Сам стоящий под корнем интеграл называется среднеквадратическим отклонением между функциями и .