Математические ожидания и ковариации векторов и матриц

3.3. Математические ожидания и ковариации векторов и матриц

При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.

В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:

у= и e=.

Значения i-й переменной у_i (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной e_i случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.

При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.

Математические ожидания

Математическое ожидание вектора у размеров пх1 случайных переменных y₁, y₂, ..., у_п определяется как вектор их ожидаемых значений:

Е(у)=Е===y,                                        (3.3.1)

Рекомендуемые материалы

где E(у_i)=y_i получается в виде E(у_i)=, используя функцию f_i(у_i) плотности вероятности безусловного распределения переменной у_i.

Если х и у - векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:

Е(х+у)=Е(х)+Е(у).                                                    (3.3.2)

Пусть у_ij (i=1, 2, ..., m; j=1, 2, ..., п) набор случайных переменных с ожидаемыми значениями E(у_ij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(y_ij) размеров mхп следующим образом:

Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов

E(Y)=[E(y_ij)].

По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:

E(Y)==.     (3.3.3)

Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.

Теорема 3.3.1. Если матрицы А=(а_ij) размеров lхm, B=(b_ij) размеров nхp, С=(c_ij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то

E(AYB+C)=AE(Y)B+C.                                         (3.3.4)

Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]

□

Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у - векторы случайных переменных размеров пх1, то

E(Aх+Bу)=AE(х)+BE(у).

Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр - все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то

E[след(AYB+C)]=след[E(AYB+C)], так как след матрицы - линейный оператор

=след[AE(Y)B+C], так как AYB+C - линейная функция матрицы Y

=след[AE(Y)B]+след(C).                                                                 (3.3.5)

Ковариации и дисперсии

Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.

Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов

C(х, у)=[C(х_i, у_j)].

Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация

C(х, у)=E[(x–x)(y–y)^T].

Доказательство:

C(х, у)=[C(х_i, у_j)]

={E[(х_i–x_i)(y_j–y_j)]}               [в силу (3.2.9)]

=E[(x–x)(y–y)^T].      [по определению 3.3.1]

□

Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1

C(х, у)=E[(x–x)(y–y)^T]

=E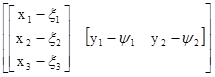

=Е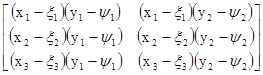

=.

Определение 3.3.3. Если х=у, то матрица ковариаций C(у, у) записывается в виде D(у)=E[(y–y)(y–y)^T] и называется матрицей дисперсий и ковариаций вектора у. Таким образом,

D(у)=E[(y–y)(y–y)^T]=[C(у_i, у_j)]

=.                (3.3.4)

А так как C(у_i, у_j)=C(у_j, у_i), то матрица (3.3.4) симметричная и квадратная.

Матрица дисперсий и ковариаций вектора у представляется в виде ожидаемого значения произведения (y–y)(y–y)^T. В силу (П.2.13), произведение (y_i–y_i)(y_j–y_j) является (ij)-м элементом матрицы (y–y)(y–y)^T. Таким образом, в силу (3.2.9) и (3.3.4), математическое ожидание E[(y_i–y_i)(y_j–y_j)]=s_ij является (ij)-м элементом Е[(y–y)(y–y)^T]. Отсюда

E[(y–y)(y–y)^T]=.                  (3.3.5)

Дисперсии s₁₁, s₂₂, ..., s_пп переменных y₁, y₂, ..., у_п и их ковариации s_ij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:

S=D(у)=                                (3.3.6)

В матрице S i-я строка содержит дисперсию переменной у_i и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением s_ij, используем для дисперсий s_ii=s_i², где i =1, 2, ..., n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(у_i, у_j)=s_ij для двух переменных.

Матрица S дисперсий и ковариаций симметричная, так как s_ij=s_ji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.

Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1

D(у)=E[(y–y)(y–y)^T]

=E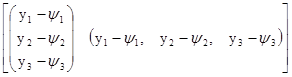

=E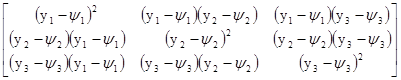

=.

=.

Как следует из определения 3.3.3,

D(у)=E[(у–y)(y–y)^T],                                              (3.3.7)

что после подобного сделанному в (3.2.4) преобразованию приводится к выражению

D(y)=E(yy^T)–yy^T.                                                    (3.3.8)

Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).

Пример 3.3.1. Если а - какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то

D(y–а)=D(y).

Это следует из того, что y_i–a_i–E(y_i–a_i)=y_i–a_i–E(y_i)+a_i=y_i–E(y_i), так что

C(y_i–a_i, y_j–a_j)=C(y_i, y_j).

□

Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма у^ТАу>0. В дальнейшем будет использоваться часто следующая теорема.

Теорема 3.3.3. Если у - вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что а^Ту=b для любого у, то D(у)=S - положительно определенная матрица.

Доказательство этой теоремы дано в [Себер (1980) стр.22].

□

Обобщенная дисперсия и нормированный вектор

Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:

Обобщенная дисперсия =det(S).                                       (3.3.9)

В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=Y^T(I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y₁, y₂, …, y_k], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:

Обобщенная выборочная дисперсия =det(S).                  (3.3.10)

Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора , чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y₁, y₂,..., у_п вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].

Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде

Нормированная разность =(у–y)^ТS^–1(у–y).                     (3.3.11)

Использование матрицы S^–1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S^–1=S^–1/2S^–1/2. Отсюда

(у–y)^ТS^–1(у–y)=(у–y)^ТS^–1/2S^–1/2(у–y)

=[S^–1/2(у–y)]^Т[S^–1/2(у–y)]

=z^Тz,

Вам также может быть полезна лекция "Построение формы в ранне многоголосии".

где z=S^–1/2(у–y) - вектор нормированных случайных переменных. Математическое ожидание вектора z получается

Е(z)=Е[S^–1/2(у–y)]=S^–1/2[Е(у)–y]=0

и его дисперсия

D(z)=D[S^–1/2(у–y)]=S^–1/2D(у–y)S^–1/2=S^–1/2SS^–1/2=S^–1/2S^1/2S^1/2S^–1/2=I.

Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S^–1/2(у–y) имеет нормальное распределение N(0, I).

Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у–)^ТS^–1(у–) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у–)^ТS^–1(у–)=а², центрированный вектором  и базирующийся на S^–1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у–)^ТS^–1(у–) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)]^1/2. Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.