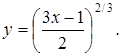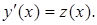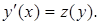Интегрирование дифференциальных уравнений n-го порядка методом понижения порядка

Интегрирование дифференциальных уравнений  n - го порядка  методом

понижения порядка

     Если правая часть уравнения (2.1) является известной непрерывной функцией от x:  f(x)   или не содержит искомую функцию y:   или не  содержит явно независимую переменную x:  то для решения уравнения (2.1)может быть применен метод понижения порядка.

     1.                               (2.2)

     Это уравнение  интегрируется  непосредственно  n  раз.  При каждом интегрировании порядок уравнения понижается на единицу, и появляется произвольная  постоянная.  В результате общее решение

уравнения будет иметь вид

             (2.3)

         ------------

       5n-кратный интеграл

Рекомендуемые материалы

    2.                        (2.4)

Уравнение (2.4) не содержит искомой функции y(x). Рассмотрим процедуру  интегрирования  уравнения  данного типа на примере уравнения второго порядка                                       (2.5)

    Понижение порядка  достигается подстановкой

                                                (2.6)     

    Тогда                              (2.7)

и уравнение (2.5) сводится к уравнению первого  порядка  относительно функции z(x):     z'(x) = f(x,z).                   (2.8)

    Интегрируя уравнение (2.8), находим его общий интеграл в виде

                                      (2.9)

где  - произвольная постоянная.  Далее в (2.9) заменяем  левую часть  согласно (2.6) и вновь получаем уравнение первого порядка относительно искомой функции y

                                    (2.10)

    Интегрируя уравнение (2.10), находим общее решение исходного уравнения (2.4) в виде

                                   (2.11)

     Замечание. Если уравнение (2.4) не содержит ни искомой функции y,  ни ее производных до (k-1) - го порядка включительно, то есть имеет вид

              

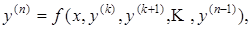
то его порядок может быть понижен сразу на k единиц подстановкой

    3.                       (2.12)

    Это уравнение не содержит явно независимой переменной  x.  В частном случае уравнение второго порядка данного типа будет

                                      (2.13)

    Понижение порядка достигается подстановкой

                                               (2.14)

                             

    Тогд                             (2.15)

( по правилу вычисления производной от сложной функции ). Поэтому уравнение  (2.13)  сводится  к уравнению первого порядка относительно функции z(y):

                                     (2.16)

    Интегрируя уравнение  (2.16),  находим  его общее решение  в виде

                                    (2.17)

где  - произвольная постоянная.  Далее в (2.17) заменяем левую часть согласно (2.14) и вновь приходим к уравнению  первого  порядка с разделяющимися  переменными относительно искомой функции

                                    (2.18)

    Интегрируя уравнение (2.18),  окончательно получим общий интеграл исходного уравнения (2.13) в виде

                                  (2.19)

    Пример.   Решить уравнение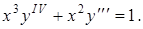  

    Это уравнение  не  содержит искомой функции y(x) и ее первых производных   и относится ко второму из рассмотренных нами типов. Применяя подстановку

                                      (2.20)

получаем линейное неоднородное уравнение  первого порядка

                                      (2.21

     Интегрируем  его методом  вариации произвольной постоянной. Сначала решаем соответствующее однородное уравнение

                                     (2.22

Разделяем в нем переменные:

                                  

После интегрирования получим

               

          

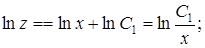
Следовательно, общее решение уравнения (2.22) будет

                    

                                         (2.23)

    Далее ищем решение уравнения (2.21) в форме,  аналогичной по структуре выражению (2.23),  но произвольную постоянную в (2.23)заменяем неизвестной функцией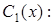

                                        (2.24)

    Подставляя (2.24) в (2.21), получим

                

откуда следует

                  

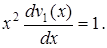
Интегрируя это уравнение, находим  Поэтому согласно (2.24) имеем

                                     (2.25)

Заменяя в выражении (2.25) z по формуле (2.20), приходим к уравнению третьего порядка относительно искомой функции y(x):

                                    (2.26)

    Уравнение (2.26)  содержит  в правой части известную функцию от x и относится к первому из рассмотренных нами типов. Интегрируя его последовательно три раза, окончательно получим общее решение исходного уравнения, содержащее 4 произвольных постоянных

        

       

    

    

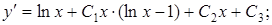
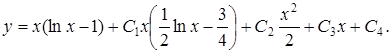
    Пример. Решить уравнение   при следующих начальных условиях:  

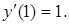
    Уравнение не содержит переменной x в явном виде и потому относится к третьему из перечисленных типов. Принимаем  тогда с учетом (2.15) уравнение примет вид                        

                  

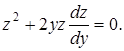
Сокращаем на  ( решение z=0, то есть , y=C нужно исследовать отдельно ).

                     

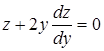
     Это уравнение с разделяющимися переменными:

                   

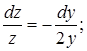
Интегрируя, получим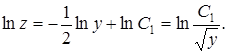

Отсюда следует   

                                         (2.27)

   Определим произвольную постоянную  Подставляя (2.27) во второе начальное условие, получим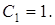  

    С учетом (2.14) уравнение (2.27) принимает вид

                        

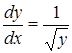
Ещё посмотрите лекцию "Переход газопровода через водную преграду" по этой теме.

    Разделяя переменные,  имеем  следовательно, после интегрирования получаем

                     

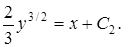
Находим  из первого начального условия: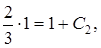  

следовательно   Поэтому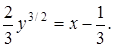 

     Возводя обе  части  этого равенства в степень 2/3,  получим окончательно решение задачи Коши в виде