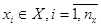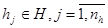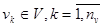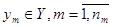Основные понятия теории моделирования

Основные понятия теории моделирования.

Пусть задана сложная дискретная система S.

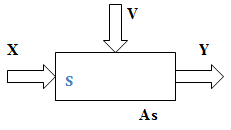
Модель объекта моделирования можно представить в виде множества величин, определяющих процесс функционирования реальной системы S и образующие в общем случае следующие подмножества:

 В общем случае эти переменные (,,) являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.

При моделировании функционирования сложной системы S, входные воздействия Х, воздействия внешней среды М и внутренние параметры системы являются независимыми (экзогенными) характеристиками (или переменными), которые в векторной форме имеют следующий вид:

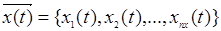
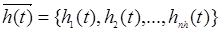
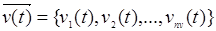
А выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют следующий вид:

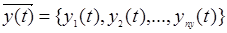
Процесс функционирования системы S описывается по времени некоторым оператором F_s, который в общем случае преобразует независимые переменные в соответствии со следующим соотношением:

                                                          (1)

Эта зависимость (1) называется законом функционирования сложной системы S. В общем случае он может быть задан в виде функции, функционала, логических условий, в алгоритмическом или табличном виде и т.д. Весьма важным является понятие алгоритма функционирования системы, под которым подразумевается метод получения выходных характеристик y(t) с учетом входных воздействий x(t), воздействий внешней среды v(t) и соответствующих внутренних параметров системы h(t). Очевидно, что один и тот же закон функционирования F_s может быть реализован различными способами, т.е. с помощью множества различных алгоритмов функционирования. Соотношение (1) может быть получено и через свойства системы в конкретные моменты времени, называемыми состояниями, которые характеризуют вектор состояний:

Ещё посмотрите лекцию "5. Влажность воздуха. Облака. Осадки. " по этой теме.

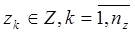
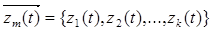
Если рассматривать процесс функционирования системы как последовательную смену состояний , то они могут быть интерпретированы как координаты точки в k-мерном пространстве (фазовом пространстве), причем каждой реализации процесса будет соответствовать некоторая траектория – совокупность всех возможных состояний . Совокупность всех возможных состояний  называется пространством состояния объекта.

Состоянием системы в момент времени t₀ ≤ t ≤ T* полностью определяется начальными условиями , где Z⁰ – состояние системы в момент времени t₀, входными воздействиями, внутренними параметрами и воздействиями внешней среды, которые имели место за промежуток времени (t – t₀). Определим их с помощью двух векторных уравнений:

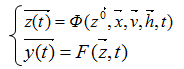
В общем случае время в модели может быть непрерывным в интервале t₀ ≤ t ≤ T*, а может быть и дискретным, т.е. квантованным на отрезке ∆t: T* = m∆t, где m - число интервалов дискретизации.