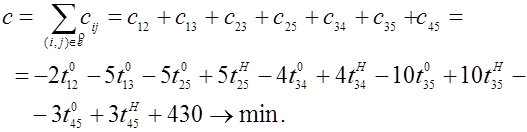Оптимизация комплекса операций
Оптимизация комплекса операций
А. Оптимизация комплекса операций по времени
Оптимизация комплекса операций по времени сводится к сокращению продолжительности критического пути. Необходимость проведения оптимизации сетевого графика по времени возникает тогда, когда критическое время выполнения комплекса операций превосходит срок  , на котором настаивает ЛПР. Очевидно, подобная задача требует проведения определенных мероприятий и (или) вложения дополнительных средств.
, на котором настаивает ЛПР. Очевидно, подобная задача требует проведения определенных мероприятий и (или) вложения дополнительных средств.
Иногда оптимизация достигается за счет перепланировки сетевого проекта (изменения топологии сети). Например, одновременно выполняемые операции, имеющие резервы времени и не лежащие на критическом пути могут выполняться последовательно (если это допускается технологией). Освободившиеся при этом ресурсы можно использовать на критических операциях, что ускорит их выполнение. Сокращение времени выполнения операций возможно также за счет автоматизации производственных процессов, улучшения организации работ, использования передовых технологий и т.д.
Оптимизация комплекса операций по времени может проводиться с привлечением дополнительных средств и с использованием внутренних резервов.
Приведем математическую формулировку процесса оптимизации по времени.
Пусть задан сетевой график выполнения комплекса операций. Время выполнения каждой операции равно  . Пусть также вложение
. Пусть также вложение  дополнительных средств в операцию
дополнительных средств в операцию  сокращает время выполнения с
сокращает время выполнения с  до
до  . Естественно, для каждой операции существует минимально возможное время ее выполнения, равное
. Естественно, для каждой операции существует минимально возможное время ее выполнения, равное  . Требуется определить время начала
. Требуется определить время начала  и окончания
и окончания  выполнения операций, а также величину дополнительных средств
выполнения операций, а также величину дополнительных средств  , которые необходимо вложить в каждую из операций
, которые необходимо вложить в каждую из операций  , чтобы общее время выполнения комплекса операций было минимальным. При этом сумма вложенных дополнительных средств не должна превышать заданной величины
, чтобы общее время выполнения комплекса операций было минимальным. При этом сумма вложенных дополнительных средств не должна превышать заданной величины , а время выполнения каждой операции должно быть не меньше минимально возможного времени
, а время выполнения каждой операции должно быть не меньше минимально возможного времени  .
.
Математически условия задачи можно записать следующим образом:
 (3.1)
(3.1)
Рекомендуемые материалы
 (3.2)
(3.2)
 (3.3)
(3.3)
 (3.4)
(3.4)
 ; (3.5)
; (3.5)
 . (3.6)
. (3.6)
Добавив при необходимости фиктивную операцию, выходящую из последнего события, целевую функцию любого графика можно записать в виде выражения (3.1).
Ограничения-равенства (3.4) показывают зависимость продолжительности выполнения операций от вложенных средств. Ограничения (3.5) обеспечивают выполнение условий предшествования операций в соответствии с топологией сети (время начала выполнения каждой операции должно быть не меньше времени окончания непосредственно предшествующей ей операции).
Критический путь  в данной задаче является функцией от объемов дополнительно вкладываемых средств
в данной задаче является функцией от объемов дополнительно вкладываемых средств  .
.
Сформулированная задача относится к классу оптимизационных задач и может быть решена методами линейной или нелинейной оптимизации в зависимости от вида функций  .
.
Приведем пример решения задачи оптимизации комплекса операций по времени путем затрат дополнительных средств.
Пример 1.
Комплекс операций представлен сетевым графиком (рис. 3.6). Цифры, приписанные дугам, означают соответственно продолжительность  и минимально возможное время
и минимально возможное время  выполнения операций (в днях).
выполнения операций (в днях).
Продолжительность выполнения операций зависит линейно от дополнительно вложенных средств и выражается соотношением
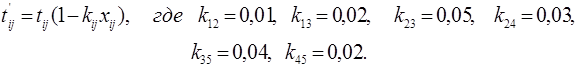
Требуется оптимизировать сетевой график по времени, т.е. определить время выполнения каждой операции сетевого графика таким образом, чтобы время выполнения комплекса операций было минимальным, а сумма вложенных средств  не превышала 15 единиц.
не превышала 15 единиц.
Решение
Добавив на сетевом графике фиктивную операцию (5,6), запишем целевую функцию в виде:
 .
.
Запишем ограничения задачи:
сумма вложенных средств не должна превышать наличного их количества:
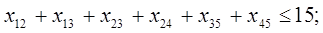
время выполнения каждой операции должно быть не меньше минимально возможного времени:
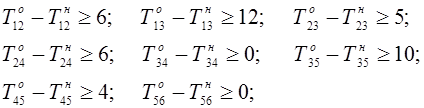
зависимость продолжительностей операций от вложенных средств дает ограничения-равенства:
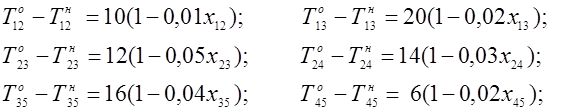
время начала выполнения каждой операции должно быть не меньше времени окончания непосредственно предшествующей ей операции (моменты времени 
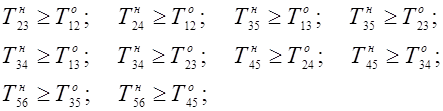
условие неотрицательности неизвестных:

для всех дуг сетевого графика.
Создадим на рабочем листе Excel форму для ввода данных, необходимых для решения задачи (Рис. 3.7).
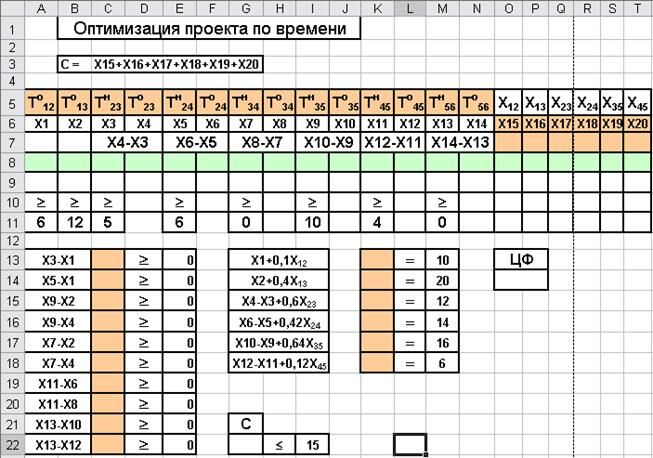
Рис. 3.7. Форма для ввода данных примера 1.
Введем обозначения для переменных согласно Рис. 3.7, и отведем под расчетные значения X1-X20 диапазон ячеек A8:T8. Далее, введем формулы для расчета функций-ограничений в соответствии с приводимой ниже таблицей
| Ячейка | Формула | Ячейка | Формула |
| C9 | =D8-C8 | K13 | =A8+0,1*O8 |
| E9 | =F8-E8 | K14 | =B8+0,4*P8 |
| G9 | =H8-G8 | K15 | =D8-C8+0,6*Q8 |
| I9 | =J8-I8 | K16 | =F8-E8+0,42*R8 |
| K9 | =L8-K8 | K17 | =J8-I8+0,64*S8 |
| M9 | =N8-M8 | K18 | =L8-K8+0,12*T8 |
| C13 | =C8-A8 | ||
| C14 | =E8-A8 | G22 | =O8+P8+Q8+R8+S8+T8 |
| C15 | =I8-B8 | ||
| C16 | =I8-D8 | O14 | =N8 |
| C17 | =G8-B8 | ||
| C18 | =G8-D8 | ||
| C19 | =K8-F8 | ||
| C20 | =K8-H8 | ||
| C21 | =M8-J8 | ||
| C22 | =M8-L8 |
Целевой ячейкой является O14.
Вызываем Поиск решения и вводим все необходимые ограничения.
Ответ:
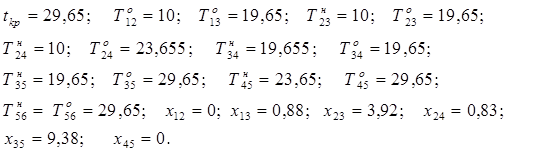
Таким образом, чтобы выполнить комплекс операций за 29,65 дней, необходимо вложить в операцию (1,3) 0,88 д.е., в операцию (2,3) 3,92 д.е., в (2,4) 0,83 д.е., и в операцию (3,5) - 9,38 д.е..
Б. Оптимизация комплекса операций по стоимости при фиксированном сроке выполнения проекта
Рассмотрим частный случай оптимизации комплекса операций по стоимости (затратам). Будем предполагать, что затраты на выполнение отдельных операций находятся в обратной зависимости от продолжительности их выполнения. Коэффициент дополнительных затрат (КДЗ)  этой зависимости для операции
этой зависимости для операции  вычисляется по формуле
вычисляется по формуле
 , (3.7)
, (3.7)
где  – срочный режим выполнения операции (наименьшая продолжительность), которому соответствуют наибольшие затраты
– срочный режим выполнения операции (наименьшая продолжительность), которому соответствуют наибольшие затраты  ;
;  – нормальный режим выполнения операции (наибольшая продолжительность), которому соответствуют минимальные затраты
– нормальный режим выполнения операции (наибольшая продолжительность), которому соответствуют минимальные затраты  .
.
Коэффициент дополнительных затрат показывает, насколько увеличится стоимость операции при уменьшении продолжительности на единицу времени.
Отличительная особенность оптимизации при фиксированном сроке выполнения комплекса операций заключается в том, что в исходном варианте сети оценки для каждой операции установлены на уровне минимальных продолжительностей  и максимальных затрат
и максимальных затрат  . Следовательно, стоимость выполнения всего комплекса операций является максимальной. Предполагается, что увеличение продолжительности операции
. Следовательно, стоимость выполнения всего комплекса операций является максимальной. Предполагается, что увеличение продолжительности операции  на 1 ед. вызывает уменьшение стоимости на величину
на 1 ед. вызывает уменьшение стоимости на величину  . Таким образом, ставится задача: при фиксированном сроке завершения
. Таким образом, ставится задача: при фиксированном сроке завершения  минимизировать стоимость выполнения комплекса операций, используя резервы времени. Критическое время
минимизировать стоимость выполнения комплекса операций, используя резервы времени. Критическое время  может быть меньше заданного срока
может быть меньше заданного срока  или равно ему. Если
или равно ему. Если  , то оптимизация возможна за счет увеличения времени выполнения некритических операций; если
, то оптимизация возможна за счет увеличения времени выполнения некритических операций; если  , то оптимизировать можно за счет всех операций комплекса.
, то оптимизировать можно за счет всех операций комплекса.
Рассмотрим более общий случай, когда  .
.
Обозначим стоимость выполнения операции  через
через  . Исходя из условия задачи, стоимость каждой операции
. Исходя из условия задачи, стоимость каждой операции  за время ее выполнения
за время ее выполнения  определим по формуле
определим по формуле
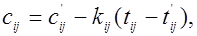

 (3.8)
(3.8)
где  . Учитывая, что величины
. Учитывая, что величины  известны, раскроем скобки в правой части (3.8) и обозначим через
известны, раскроем скобки в правой части (3.8) и обозначим через  сумму
сумму  . В результате получим
. В результате получим  . Здесь время выполнения операции
. Здесь время выполнения операции  равно разности между временем ее окончания
равно разности между временем ее окончания  и временем начала
и временем начала  .
.
Математическая модель задачи может быть сформулирована следующим образом: найти такое время начала и окончания каждой операции сетевого графика, при котором стоимость выполнения комплекса операций будет минимальной:
 .
.
На неизвестные величины задачи налагаются следующие ограничения:
продолжительность выполнения каждой операции должна быть не меньше  и не больше
и не больше  :
:
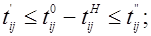
время окончания любой операции сетевого графика должно быть не больше времени начала непосредственно следующей за ней операции, т.е. для любых смежных операций сети  и
и  должно выполняться условие
должно выполняться условие
 ;
;
выполнение комплекса операций должно быть завершено не позже директивного срока  :
:
 ;
;  - номер завершающего события;
- номер завершающего события;
переменные должны быть неотрицательными:
 ;
;  для всех
для всех  , при этом
, при этом  ,
,  .
.
Рассмотрим пример оптимизации проекта по стоимости за счет увеличения продолжительности отдельных операций.
Пример 2.
Исходные данные комплекса операций, представленного сетевым графиком (рис. 3.8), приведены в Табл. 3.2. Требуется оптимизировать сетевой график по стоимости при  .
.
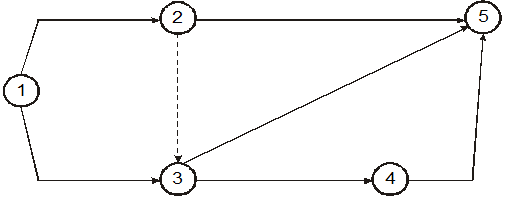
Рис. 3.8. Сетевой график примера 2.
Таблица 3.2.
| Параметры | Операции | ||||||
| (1,2) | (1,3) | (2,3) | (2,5) | (3,4) | (3,5) | (4,5) | |
|
| 9 | 10 | 0 | 3 | 4 | 5 | 8 |
|
| 11 | 15 | 0 | 5 | 7 | 8 | 10 |
|
| 2 | 5 | - | 5 | 4 | 10 | 3 |
|
| 20 | 40 | - | 30 | 45 | 50 | 25 |
Решение
Запишем  , для всех
, для всех  , принадлежащих сетевому графику:
, принадлежащих сетевому графику:
|
|
|
|
|
|
|
|
|
| ||
|
|
При записи функции принято, что  . Так как при параметрах
. Так как при параметрах 
 меньше
меньше  , то оптимизация возможна за счет всех операций сетевого графика. Запишем ограничения по времени выполнения операций:
, то оптимизация возможна за счет всех операций сетевого графика. Запишем ограничения по времени выполнения операций:


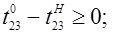
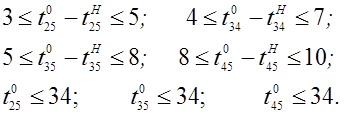
Ограничения по предшествованию в выполнении операций:
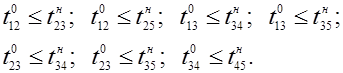
Все неизвестные должны быть неотрицательными, т.е.  для всех операций
для всех операций  сети.
сети.
Проведем решение задачи в Excel. Введем данные на рабочий лист в соответствии с Рис. 3.9.
Для расчетных значений переменных X1-X12 отведем диапазон ячеек A5:L5. Далее, введем функции-ограничения и формулу для целевой функции в ячейки в соответствии с приводимой ниже таблицей.
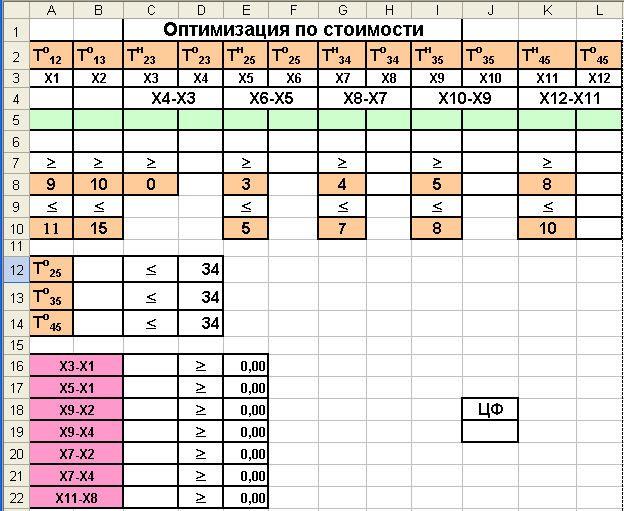
Рис. 3.9. Форма для ввода данных примера 2.
| Ячейка | Формула | Ячейка | Формула |
| C6 | =D5-C5 | C16 | =C5-A5 |
| E6 | =F5-E5 | C17 | =E5-A5 |
| G6 | =H5-G5 | C18 | =I5-B5 |
| I6 | =J5-I5 | C19 | =I5-D5 |
| K6 | =L5-K5 | C20 | =G5-B5 |
| B12 | =F5 | C21 | =G5-D5 |
| B13 | =J5 | C22 | =K5-H5 |
| B14 | =L5 | ||
| J19 (целевая функция) | = -2*A5-5*B5-5*F5+5*E5-4*H5+4*G5-10*J5+10*I5-3*L5+3*K5+430 |
При решении данной задачи наибольшую сложность представляет ввод ограничений на переменные, число которых достаточно велико. Вызовем Поиск решения и введем следующий набор ограничений
| $A$5<=$A$10 | $E$6<=$E$10 | $H$5>=14 | $C$16>=$E$16 |
| $A$5>=$A$8 | $E$6>=$E$8 | $I$5>=10 | $C$17>=$E$17 |
| $B$5<=$B$10 | $G$6>=$G$8 | $J$5>=15 | $C$18>=$E$18 |
| $B$5>=$B$8 | $G$5>=10 | $I$6<=$I$10 | $C$19>=$E$19 |
| $C$5>=9 | $G$6<=$G$10 | $I$6>=$I$8 | $C$20>=$E$20 |
| $C$6>=$C$8 | $F$5<=34 | $K$6<=$K$10 | $C$21>=$E$21 |
| $D$5>=9 | $J$5<=34 | $K$6>=$K$8 | Вам также может быть полезна лекция "12. Истолкование уравнения Д. Бернулли". $C$22>=$E$22 |
| $E$5>=9 | $L$5<=34 |
В результате решения получим ответ:
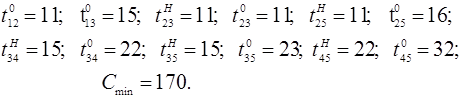
Таким образом, при заданном сроке выполнения проекта  минимальная стоимость его реализации составляет 170 д.е.
минимальная стоимость его реализации составляет 170 д.е.



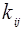
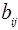
 ;
; ;
; ;
; ;
; ;
; ;
; ;
;