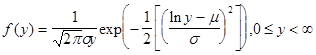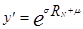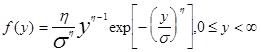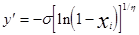Моделирование нормально распределённой случайной величины y
Моделирование нормально распределённой случайной величины y.
Оно может быть осуществлено на основании центральной предельной теоремы, согласно которой закон распределения суммы независимых случайных величин стремится к нормальному с увеличением числа слагаемых. Для решения некоторых задач практически сумму  значений, выданных с генератором случайных чисел с характеристиками f(xi)=1, 0£xi£1, mx=0.5,
значений, выданных с генератором случайных чисел с характеристиками f(xi)=1, 0£xi£1, mx=0.5,  .
.
Можно считать значениями распределённой случайной величины  при n³8. Так как все слагаемые xi имеют одинаковые математические ожидания mx и дисперсии Dx, то my=nmx, Dy=nDx. В таблице 1 приведены формулы для расчёта случайных величин для различных видов распределений на базе случайной величины с равномерным распределением.
при n³8. Так как все слагаемые xi имеют одинаковые математические ожидания mx и дисперсии Dx, то my=nmx, Dy=nDx. В таблице 1 приведены формулы для расчёта случайных величин для различных видов распределений на базе случайной величины с равномерным распределением.
Получение случайной величины с различными распределениями.
Таблица 1.



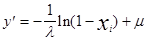
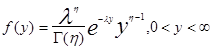
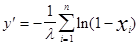
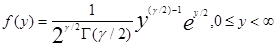
 RN - нормированная случ. величина с нормальным законом распределения
RN - нормированная случ. величина с нормальным законом распределения