Элементы векторной алгебры и аналитической геометрии
Глава 2. Элементы векторной алгебры и аналитической геометрии.
§1. Линейные операции над векторами.
Геометрический вектор 
 - представитель
- представитель  Длина ( модуль )
Длина ( модуль ) 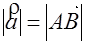
Нулевой вектор 
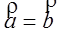
1. Сумма векторов 

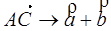
2. Умножение вектора  на вещественное число k - это вектор
на вещественное число k - это вектор 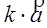
1)  2)
2)  при k>0
при k>0  при k<0
при k<0
Свойства. 1.  2.
2.  3.
3.  4.
4.
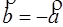
5. 
 разность 6.
разность 6.  7.
7. 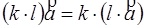
Рекомендуемые материалы
8.  9.
9. 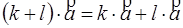

 орт (единичный вектор)
орт (единичный вектор)
Система векторов  линейно зависимая, если
линейно зависимая, если  :
: 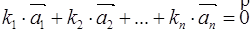
Свойства. 1.  линейно зависимая
линейно зависимая  они коллинеарны.
они коллинеарны.
2.  линейно зависимая
линейно зависимая  они компланарны.
они компланарны.
§2. Базис и координаты вектора.
 - базис (на прямой),
- базис (на прямой), 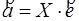
 - базис (на плоскости)
- базис (на плоскости) 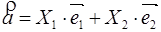
 - базис (в пространстве)
- базис (в пространстве)  (1) Х1,Х2,Х3 - координаты
(1) Х1,Х2,Х3 - координаты
(1) – разложение вектора по базису Разложения единственны (см. 9 и 11 кл.)
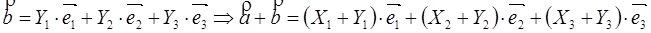
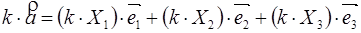
Прямоугольный базис 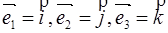
 и ось l
и ось l  - составляющая вектора по оси.
- составляющая вектора по оси. 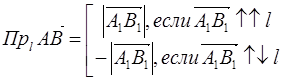
Свойства проекции. 1.  2.
2. 3.
3.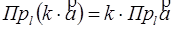
§3. Декартова прямоугольная система координат.
( О, Е ) 1) О – начало координат 2) прямоугольный базис 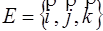
Ox, Oy, Oz – координатные оси
 – радиус-вектор точки М
– радиус-вектор точки М
Теорема.  Oxyz
Oxyz 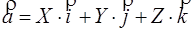
Свойства. Если  , то
, то
1.  2.
2.  3.
3. 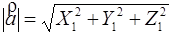
4. 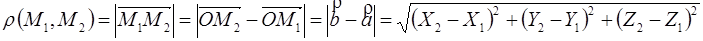
5. Если  и
и  , то
, то  - деление отрезка в заданном отношении.
- деление отрезка в заданном отношении.
§4. Скалярное произведение векторов.
( a,b ) = a . b = 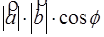
Свойства.
1. Если  , то f – острый
, то f – острый  a . b>0 f – тупой
a . b>0 f – тупой  a . b<0 f – прямой
a . b<0 f – прямой  a . b=0
a . b=0
2.  3. a . b=b . a 4. (ka) . b = k(a,b) 5. (a + b) . c = a . c + b . c
3. a . b=b . a 4. (ka) . b = k(a,b) 5. (a + b) . c = a . c + b . c
Теорема. Если а ( X1, Y1, Z1 ), b (X2, Y2, Z2 ) , то a . b = X1X2+Y1Y2+Z1Z2
Следствия. 1. 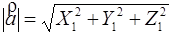
2. Условие перпендикулярности ( ортогональности) a,b X1X2+Y1Y2+Z1Z2 = 0
3. 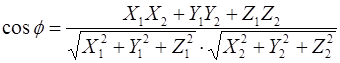
§5. Направляющие косинусы вектора.
Oxyz  Углы с осями a,b,g
Углы с осями a,b,g 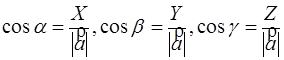

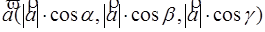
§6. Прямая на плоскости.
1. Ах + Ву + С = 0 - общее уравнение прямой
2. А(х-х0) + В(у-у0) = 0 через точку М(х0, у0) перпендикулярно нормальному вектору n(A,B)
3.  через точку М(х0, у0) параллельно направляющему вектору q ( l, m )
через точку М(х0, у0) параллельно направляющему вектору q ( l, m )
4. y = kx + b k – угловой коэффициент, b – начальная ордината.
5.  параметрические уравнения прямой
параметрические уравнения прямой 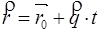
6.  в отрезках
в отрезках
7. x cosa + y cosb – p = 0 нормальное уравнение
Формулы. 1. 
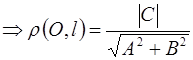
2.  3.
3. 
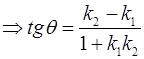
Условие параллельности k1 = k2 Условие перпендикулярности k1.k2 = -1
§7. Полярные координаты.
( О, р ) О – полюс Луч р – полярная ось
Полярные координаты точки  - 2 числа: полярный радиус r ( M ) =
- 2 числа: полярный радиус r ( M ) =  и полярный угоп f ( M ) M ( r, f )
и полярный угоп f ( M ) M ( r, f )  - главное значение угла
- главное значение угла

 полярные – декартовы прямоугольные
полярные – декартовы прямоугольные
Уравнение кривой: F ( r, f ) = 0 или r = f ( f )
Параметрические координаты 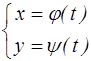
§8. Плоскость в трехмерном пространстве.
Р Oxyz
1. Ax + By + Cz + D = 0 – общее уравнение
2. A(x – x0) + B(y – y0) + C(z – z0) = 0 - уравнение плоскости, проходящей через точку M(x0,y0,z0) перпендикулярно нормальному вектору 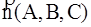
3.  - уравнение плоскости в отрезках
- уравнение плоскости в отрезках
4. x.cos a + y.cos b + z.cos g – p = 0 – нормальное уравнение плоскости.
Формулы. 1. Плоскость, параллельная 2 векторам a1 (X1, Y1, Z1), a2(X2, Y2, Z2),
имеет нормальный вектор n = 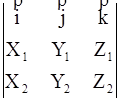

2. Косинус угла между плоскостями A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0

§9. Прямая в трехмерном пространстве.
1.  - общие уравнения (пересечение двух плоскостей)
- общие уравнения (пересечение двух плоскостей)
2. 
 q – направляющий вектор прямой
q – направляющий вектор прямой
параметрические уравнения
3.  - канонические уравнения
- канонические уравнения
Формулы. 1. Косинус угла между прямыми  и
и 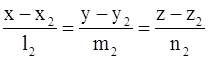
2. Синус угла между прямой  и плоскостью
и плоскостью
Ax + By + Cz + D = 0
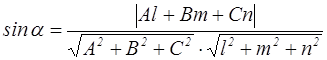
§10. Полезные формулы (для решения задач).
1. Условие перпендикулярности двух плоскостей A1A2 + B1B2 + C1C2 = 0
2. Условие параллельности двух плоскостей 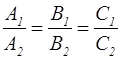
3. Условие перпендикулярности двух прямых l1l2 + m1m2 + n1n2 = 0
4. Условие параллельности двух прямых 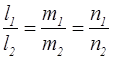
5. Расстояние от точки M(x0,y0,z0) до плоскости Ax + By + Cz + D = 0
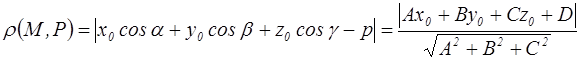
6. Уравнение прямой, проходящей через две заданные точки 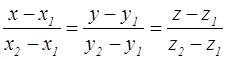
7. Если 3 точки A(x1,y1,z1), B(x2,y2,z2), C(x3,y3,z3) не лежат на одной прямой, то уравнение определяемой ими плоскости 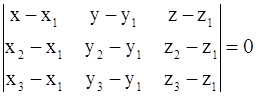
8. Условие перпендикулярности прямой и плоскости 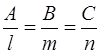
9. Условие параллельности прямой и плоскости A l + B m + C n = 0
10. Объем параллелепипеда с вершинами A(x1,y1,z1), B(x2,y2,z2), C(x3,y3,z3), D(x4,y4,z4) и ребрами AB, AC, AD 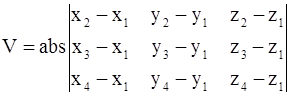
§11. Описание геометрических образов.
f ( x, y ) = 0 линия на плоскости
Неравенство f ( x, y ) ≤ 0 ( f ( x, y ) < 0 - исключая точки линии )
В трехмерном пространстве f ( x, y, z ) = 0 поверхность
 линия
линия
f ( x, y, z ) < 0 f ( x, y, z ) > 0 f ( x, y, z ) = 0
f ( y, z ) = 0 цилиндрическая поверхность, параллельная Ох.
Линейные образы
§12. Двумерная задача линейного программирования (транспортная).
3 дома, 2 бетономешалки (А, Б). Ежедневно: 1-й дом – 16 машин, 2-й – 14, 3-й – 10. А отправляет 25 машин, Б – 15. Стоимость доставки 1 машины – в таблице:
| Бетономешалки/ дома | 1 | 2 | 3 |
| А | 3 | 4 | 6 |
| Б | 3 | 5 | 2 |
Требуется составить наиболее экономный план перевозок. х: А – 1, у: А – 2
Р = 3х + 4у + 6(25 – х – у) + 3(16 – х) + 5(14 – у) + 2(х + у - 15) = 238 – 4х – 5у
Вершины многоугольника (1,14), (11, 14), (16,9), (16,0), (15,0).
Линия уровня, проходящая через точку (10,10) 238 – 4х – 5у = 148 или 4х + 5у = 90.
Линия уровня, проходящая через точку (12,12) 238 – 4х – 5у = 130 или 4х + 5у = 108.
Таблица перевозок
| Бетономешалки/ дома | 1 | 2 | 3 |
| А | 11 | Ещё посмотрите лекцию "Вещества вторичного синтеза" по этой теме. 14 | 0 |
| Б | 5 | 0 | 10 |




















