Решение систем линейных алгебраических уравнений прямыми методами

Тема  2.  Решение  систем  линейных  алгебраических  уравнений  прямыми  методами.

Системами  линейных  алгебраических  уравнений   (сокращенно  -  СЛАУ)  называются  системы  уравнений  вида

                                         (2.1)

или,  в  матричном  виде, 

                            A×x = B,                                                                                   (2.2)

где  :

   A   -  матрица  коэффициентов  системы  размерности  n´n

    x  -  вектор  неизвестных,  состоящий  из  n  компонент

Рекомендуемые материалы

   B  -   вектор  правых  частей  системы,  состоящий  из n  компонент.

             A=              x=                  B=                              (2.3)

         Решением  СЛАУ  является  такой  набор  из  n  чисел,  который  будучи  подставленным  вместо  значений  x₁, x₂, … , x_n  в  систему  (2.1)  обеспечивает  равенство  левых  частей  правым  во  всех  уравнениях.

         Каждая  СЛАУ  в  зависимости  от  значений  матриц  A  и  B  может  иметь

- одно  решение

- бесконечно  много  решений

- ни  одного  решения.

В  данном  курсе  будем  рассматривать  только  те  СЛАУ,  которые  имеют  единственное  решение.  Необходимым  и  достаточным  условием  этого  является  неравенство  нулю  определителя  матрицы  A.

         Для  поиска  решений  над  системами  линейных  алгебраических  уравнений  могут  проводиться  некоторые  преобразования,  не  изменяющие  ее  решений.  Эквивалентными  преобразованиями  системы  линейных  уравнений  называются  такие  ее  преобразования,  которые  не  изменяют  ее  решения.  К их  числу  относятся :

- перестановка  местами  двух  любых  уравнений  системы  (следует  отиетить,  что  в  некоторых  случаях,  рассматриваемых  ниже,  это  преробразование  использовать  нельзя);

- умножение  (или  деление)  какого-либо  уравнения  системы  на  число,  не  равное  нулю;

- прибавление  к  одному  уравнению  системы  другого  ее  уравнения,  умноженного  (или  разделенного)  на  некоторое  не  равное  нулю  число.

            Методы  решения  СЛАУ  делятся  на  две  больших  группы,  называемые  -  прямые  методы  и  итерационные  методы.   Имеется  также  способ  сведения  задачи  решения  СЛАУ  к  задаче  поиска  экстремума  функции  нескольких  переменных  с  последующем  решением  ее  методами  поиска  экстремума  (об  этом  подробнее  -  при  прохождении  соответствующей  темы).  Прямые  методы  обеспечивают  получение  точного  решения  системы  (если  оно  существует)  за  один  шаг.  Итерационные  методы  (если  при  этом  обеспечена  их  сходимость)  позволяют  многократно  улучшать  некоторое  начальное  приближение  к  искомому  решению  СЛАУ  и,  вообще  говоря,  точного  решения  не  дадут  никогда.  Однако,  учитывая  то,  что  прямые  методы  решения  из-за  неизбежных  ошибок  округления  на  промежуточных  этапах  расчетов  тоже  дают  не  идеально  точные  решения,  итерационные  методы  могут  тоже  обеспечить  примерно  такой  же  результат.

Прямые  методы  решения  СЛАУ.   Наиболее  часто  используемыми  прямыми  методами  решения  СЛАУ  являются :

- метод  Крамера,

- метод  Гаусса   (и  его  модификация  -  метод  Гаусса-Жордана)

- матричный  метод  (с  использованием  обращения  матрицы A).

Метод  Крамера  основан  на  вычислении  определителя  основной  матрицы   A  и  определителей  матриц   A₁,  A₂,  …,  A_n,  которые  получаются  из  матрицы  A  заменой  в  ней   одного  (i-го)  столбца  (i = 1, 2,…, n)   на  столбец,  содержащий  элементы  вектора  B.  После  этого  решения  СЛАУ  определяются  как  частное  от  деления  значений  этих  определителей.  Точнее,  расчетные  формулы  имеют  такой  вид

                                                                                      (2.4)

Пример  1.   Найдем  методом  Крамера  решение  СЛАУ,  у  которой

                               A = ,                        B = .        

Имеем

  A₁ = ,      A₂ = ,       A₃ = ,        A₄ = .

Вычислим  значения  определителей  всех  пяти  матриц  (c  использованием  функции  МОПРЕД  среды  Excel).  Получим

Так  как  определитель  матрицы  A  не  равен  нулю  -  система  имеет  единственное  решение.  Тогда  определим  его  по  формуле  (2.4).   Получим

Метод  Гаусса.  Решение  СЛАУ  этим  методом  предполагает составление  расширенной  матрицы  системы  A*.  Расширенная  матрица  системы  -  это  матрица  размером  в  n  строк  и  n+1 столбцов,  включающая  в  себя  исходную  матрицу  A  c  присоединенным  к  ней  справа  столбцом,  содержащим  вектор  B.

                A* =                                                (2.4)

Здесь  a_in+1=b_i  (i = 1, 2, …, n).

Суть  метода  Гаусса  состоит  в  приведении  (посредством  эквивалентных  преобразований)  расширенной  матрицы  системы  к  треугольному  виду  (так,  чтобы  ниже  ее  главной  диагонали  находились  только  нулевые  элементы). 

                A* =   

Тогда,  начиная  с  последней  строки  и  двигаясь  вверх,  можно  последовательно  определить  значения  всех   компонент  решения.

Начало  преобразований  расширенной  матрицы  системы  к  необходимому  виду  заключается  в  просмотре  значений  коэффициентов  при   x₁   и  выборе  строки,  в  которой  он  имеет  максимальное  по  абсолютной  величине  значение  (это  необходимо  для  уменьшения  величины  вычислительной  ошибки  при  последующих  вычислениях).  Эту  строку  расширенной  матрицы  необходимо  поменять  местами  с  первой  ее  строкой  (или  же,   что  лучше,  сложить  (или  вычесть)  с  первой  строкой  и  результат  поместить  на  место  первой  строки).   После  этого  все  элементы  этой  новой  первой  строки  (в  том  числе  и  в  последнем  ее  столбце)  необходимо  разделить  на  этот  коэффициент.   После  этого  вновь  полученный  коэффициент   a₁₁   станет  равным  единице.   Дальше  от  каждой  из  оставшихся  строк  матрицы  необходимо  вычесть  ее  первую  строку,  умноженную  на  значение  коэффициента  при   x₁    в  этой  строке   (т.е.  на  величину  a_i1,   где  i=2, 3, …n).  После  этого  во  всех  строках,  начиная  со  второй  коэффициенты  при x₁   (т.е.  все  коэффициенты  a_i1   (i=2, …, n)  будут  равными  нулю.  Поскольку  мы  выполняли  только  эквивалентные  преобразования  -  решение  вновь  полученной  СЛАУ  не  будет  отличаться  от  исходной  системы.

Дальше,  оставляя  неизменной  первую  строку  матрицы,  проделаем  все  вышеописанные  действия  с  остальными  строками  матрицы  и,  в  результате, вновь  полученный  коэффициент   a₂₂   станет  равным  единице,   а  все коэффициенты   a_i2   (i=3, 4, …, n)  станут  равными  нулю.   Продолжая  аналогичные  действия,  мы  в  конечном  итоге  приведем  нашу  матрицу  к  виду,  в  котором   все  коэффициенты  a_ii = 1  (i=1, 2, …, n),  а  все  коэффициенты  a_ij = 0  (i=2, 3, …, n,  j<i).  Если  же  на  каком-то  шаге  при  поиске  наибольшего  по  абсолютной  величине  коэффициента  при   x_j   мы  не  сможем  найти  не  равного  нулю  коэффициента  -  это  будет  значить,  что  исходная  система  не  имеет  единственного  решения.  В  этом  случае  процесс  решения  необходимо  прекратить.

Если  процесс  эквивалентных  преобразований  закончился  успешно,  то  полученная  в  результате  «треуголиная»  расширенная  матрица  будет  соответствовать  такой  системе  линейных  уравнений :

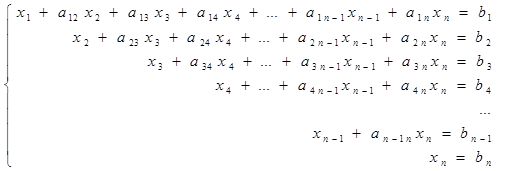
Из  последнего  уравнения  этой  системы  найдем  значение  x_n.  Далее,  подставляя  это  значение  в  предпоследнее  уравнение,  найдем  значение  x_n-1.  После  этого,  подставляя  оба  эти  найденных  значения  в  третье  снизу  уравнение  системы,  найдем  значение  x_n-2.  Продолжая  так  далее  и  продвигаясь  по  уравнением  этой  системы  снизу  вверх,  будем  последовательно  находить  значения  других  корней.  И,  наконец,  подставляя  найденные  значения  x_n,  x_n-1,  x_n-2,   ,  x₃  и  x₂  в  первое  уравнение  системы  найдем  значение  х₁.  Такая  процедура  поиска  значений  корней  по  найденной  треугольной  матрице  называется  обратным  ходом.  Процесс  приведения  исходной  расширенной  матрицы  эквивалентными  преобразованиями  к  треугольному  виду  назавают  прямым  ходом  метода  Гаусса..

         Достаточно  подробный  алгоритм  решения  СЛАУ  методом  Гаусса  приведен  на  рис. .2.1   и   рис. 2.1а.

Пример 2.   Найти  методом  Гаусса  решение  той  же  СЛАУ,  которую  мы  уже  решали  методом  Крамера.   Составим  сначала  ее  расширенную  матрицу.   Получим

                    A*  =  .        

Сначала  переставим  местами  первую  и  третью  строки  этой  матрицы  (так  как  в  ее  первом  столбце  находится  наибольший  по  абсолютной  величине  элемент),  а  затем  разделим  все  элементы  этой  новой  первой  строки  на  значение  3.  Получим

                         A* =  .

Дальше  проведем  вычитание  из  каждой  строки  матрицы  (кроме  первой)  элементов  первой  строки,  умноженных  на  коэффициент  в  первом  столбце  этой   строки.  Получим

                          A* =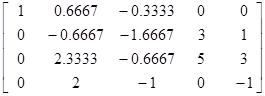 

Дальше  переставим  местами  вторую  и  третью  строки  этой  матрицы,  разделим  вторую  строку  переставленной  матрицы  на  2.3333  и,  аналогично  вышеописаному,  обнулим  коэффициенты  во  втором  столбце  третьей  и  четвертой  строк  матрицы.  Получим

                         A* =  .

После  выполнения  подобных  действий  над  третьей  и  четвертой  строками  матрицы  получим

                         A* =  .

Разделив  теперь  четвертую  строку  на  -5.3076,  закончим  проведение  расширенной  матрицы  системы  к  диагональному  виду.  Получим

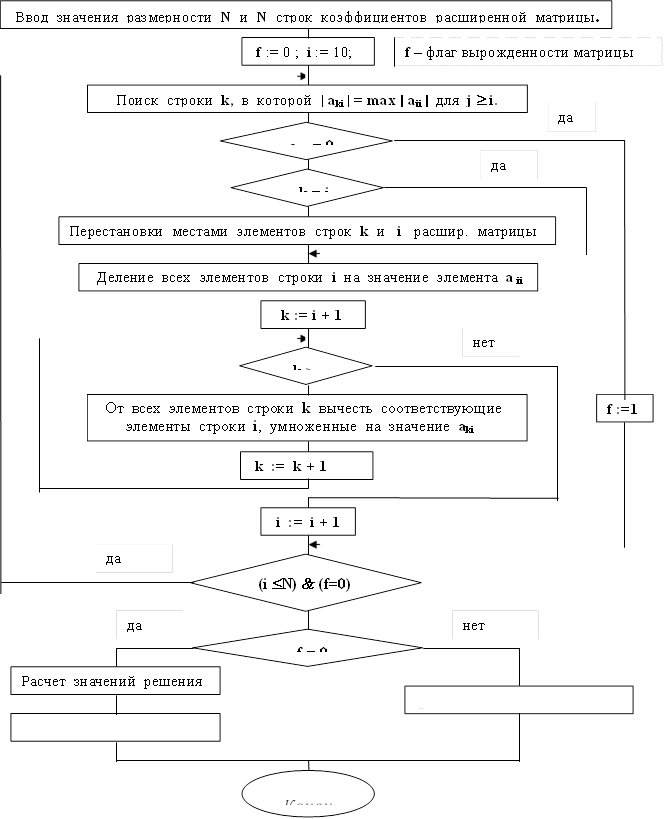Рис. 2.1.  Алгоритм  решения  систем  линейных  алгебраических  уравнений  методом  Гаусса

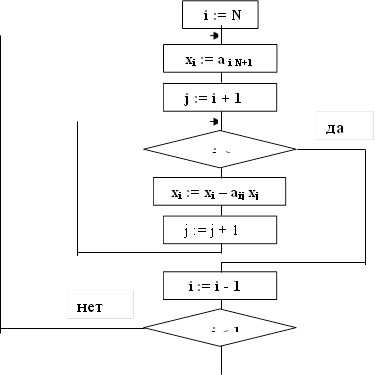Рис. 2.1а.  Макроблок  “Расчет  значений  решения”.

                         A* =  .

Из  последней  строки  сразу  получим  x₄=0.7536.  Поднимаясь  теперь  вверх  по  строкам  матрицы  и  выполняя  расчеты,  последовательно  получим   x₃=0.7971,  x₂=-0.1015  и  x₁=0.3333.   Сравнивая  полученное  этим  методом  решение  с  решением,  полученным  методом  Крамера,  нетрудно  убедиться   в  их  совпадении.

Метод  Гаусса-Жордана.  Этот  метод  решения  СЛАУ  во  многом  похож  на  метод  Гаусса.  Основным  отличием  является  то,  что  используя  эквивалентные  преобразования  расширенная  матрица  системы  уравнений  приводится  не  к  треугольному  виду,  а  к  диагональному  виду,  на  главной  диагонали  которой  находятся  единицы,  а  вне  нее  (кроме  последнего  n+1  столбца)  -  нули.  После  окончания  такого  преобразования  -  последний  столбец  расширенной  матрицы  будет  содержать  решение  исходной  СЛАУ  (т,е.  . x_i = a _{i n+1} (i=1, 2, … , n)  в  полученной  матрице).  Обратный  ход  (как  в  методе  Гаусса)  для  окончательных  расчетов  значений  компонент  решения  -  не  нужен. 

            Приведение  матрицы  к  диагональному  виду  проводится,  в  основном,  также  как  и  в  методе  Гаусса.  Если  в  строке  i  коэффициент  при  x_i  (i=1, 2, … , n)  по  абсолютной  величине  мал,  то  производится  поиск  строки  j,  в  которой  коэффициент  при  x_i  будет  наибольшим  по  абсолютной  величине  эта  (j-я)  строка  прибавляется  поэлементно  к   i-й  строке.  Затем  все  элементы   i-й  строки  делятся  на  значение  элемента x_i Но,  в  отличие  от  метода  Гаусса,  после  этого   идет  вычитание  из  каждой  строки  с  номером  j   строки  с  номером  i,   умноженной  на  a_ji,  но  условие   j > i  заменено  на  другое  В  методе  Гаусса-Жордана идет  вычитание  из  каждой  строки  с  номером  j,   причем  j # i,   строки  с  номером  i,   умноженной  на  a_ji.  Т.е.  производится  обнуление  коэффициентов  как  ниже,  так  и  выше  главной  диагонали.

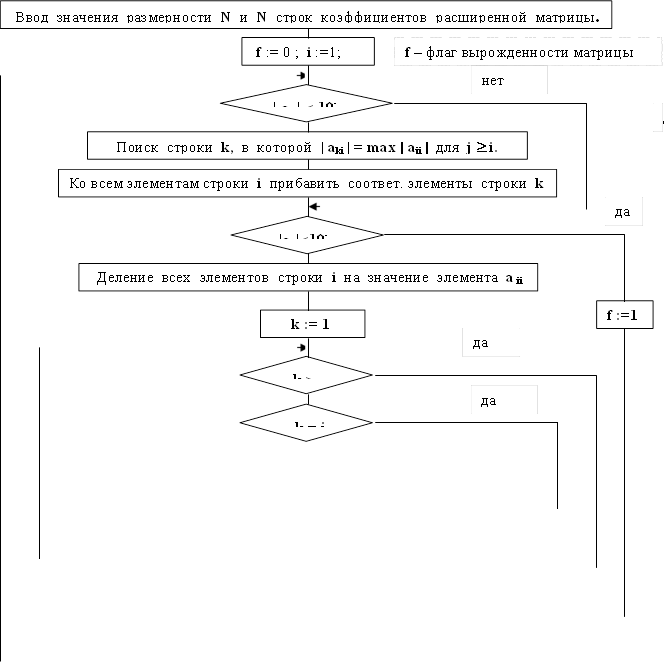
            Достаточно  подробный  алгоритм  решения  СЛАУ  методом  Гаусса–Жордана  приведен  на  рис.  2.2.

Пример  3.   Найти  методом  Гаусса-Жордана  решение  той  же  СЛАУ,  которую  мы  уже  решали  методами  Крамера  и  Гаусса.  

Полностью  аналогично  методу  Гаусса  составим  расширенную  матрицу  системы. Затем  переставим  местами  первую  и  третью  строки  этой  матрицы  (так  как  в  ее  первом  столбце  находится  наибольший  по  абсолютной  величине  элемент),  а  затем  разделим  все  элементы  этой  новой  первой  строки  на  значение  3. Дальше  проведем  вычитание  из  каждой  строки  матрицы  (кроме  первой)  элементов  первой  строки, умноженных  на  коэффициент  в  первом  столбце  этой   строки.  Получим  то  же,  что  и  в  методе  Гаусса

                               A* =  .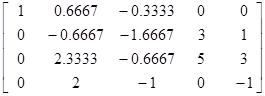

Дальше  переставим  местами  вторую  и  третью  строки  этой  матрицы,  разделим  вторую  строку  переставленной  матрицы  на  2.3333  и  (уже  в  отличие  от  метода  Гаусса)  обнулим  коэффициенты  во  втором  столбце  первой,  третьей  и  четвертой  строк  матрицы.  Получим

                               A* =  .

После  этого  разделим  все  элементы  третьей  строки  на  -1.8572,  а  затем  вычитая  из  каждой  строки  (кроме  третьей)  вновь  полученную  третью  строку,  умноженную  на  коэффициент,  стоящий  на  пересечении  этой  строки  и  третьего  столбца.  Получим

                         A* =  .

После  этого  разделим  все  элементы  четвертой  строки  на  -5.3076,  а  затем  вычитая  из  каждой  строки  (кроме  четвертой)  вновь  полученную  четвертую  строку,  умноженную  на  коэффициент,  стоящий  на  пересечении  этой  строки  и  четвертого  столбца.  Получим  окончательно

                          A* =  .

В  результате  всего  получим  диагональную  матрицу  с  единичными  элементами  по  диагонали  и  вектором  решения  в  последнем  столбце.  Решение  совпадает  с  полученным  ранее  другими  методами.

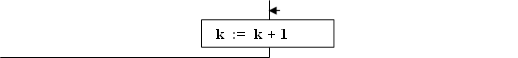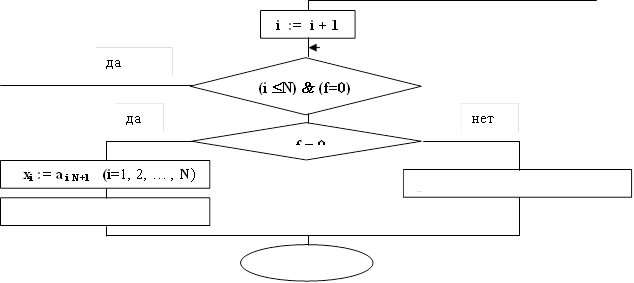Рис. 2.2.  Алгоритм  решения  систем  линейных  алгебраических  уравнений  методом  Гаусса-Жордана.

Матричный  метод  предполагает  нахождение  матрицы,  обратной  к  матрице  A  (она  обозначается  через  A^-1),  а  затем  нахождение  вектора  решения  по  формуле

                                                   x = A^-1×B.                                                                                   (2.5)

Все  вычисления  удобно  производить  в  Excel  c  использованием  функций  МОБР  и  МУМНОЖ.

Альтернативы 1917 года - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Пример  4.  Решим  тот  пример  матричным  методом.  Имеем

                                       A=,                        B=.   

Найдем  обратную  матрицу  к  матрице  A.  Получим

                                 A^-1 =  .

Теперь  по  формуле  (2.5)  получим  вектор  с  решением  нашей  СЛАУ

           x =   = .