Расчет сложных газопроводов
V РАСЧЕТ СЛОЖНЫХ ГАЗОПРОВОДОВ
Газопроводы, отличающиеся от простых, т. е. однониточных постоянного диаметра, будем называть сложными. Таковыми являются многониточные газопроводы, газопроводы с лупингами, газопроводы, состоящие из последовательно соединенных участков различного диаметра. К сложным будем относить также газопроводы, имеющие путевые отборы или подкачки.
Цель расчета сложных газопроводов такая же, как и для простых: определение либо пропускной способности, либо давлений в узловых пунктах (начальная или конечная точки, точки отборов или подкачек).
Основные расчетные формулы – те же, что и для простых газопроводов, т.е. ( ) и (
) и ( ). Эти формулы можно применять либо для отдельных ниток рассчитываемого сложного газопровода, либо в том случае, когда газопровод приведен к простому.
). Эти формулы можно применять либо для отдельных ниток рассчитываемого сложного газопровода, либо в том случае, когда газопровод приведен к простому.
Представим упомянутые формулы в более компактном виде. Входящие в них  ,
,  и
и  определяются отдельно, и их можно считать заданными. Включив эти величины в состав постоянного коэффициента
определяются отдельно, и их можно считать заданными. Включив эти величины в состав постоянного коэффициента  , получим
, получим
 (5.1)
(5.1)
 (5.2)
(5.2)
где  ;
;  .
.
Рекомендуемые материалы
При квадратичном режиме течения, если постоянные величины, содержащиеся в λ= 0,067 (2k/D)0,2, ввести в коэффициент  , формулы (5.1) и (5.2) примут вид
, формулы (5.1) и (5.2) примут вид
 (5.3)
(5.3)
 (5.4)
(5.4)
V.I Однониточный газопровод с путевыми отборами и подкачками
Пусть газопровод состоит из участков, границами которых служат пункты отборов (подкачек). Будем считать, что эти участки – простые трубопроводы (рис. 5.1).
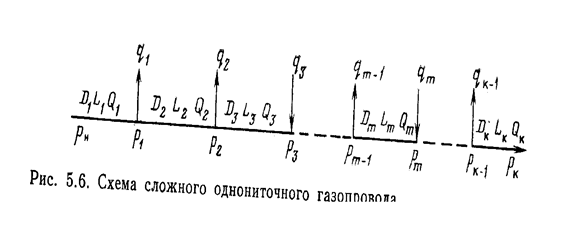
Рис. 5.1. Схема сложного однониточного газопровода
Отборы (подкачки)  ,
,  ,
,  и т. д. заданы, известны, следовательно, расходы на участках будут
и т. д. заданы, известны, следовательно, расходы на участках будут  ,
,  ,
,  и т. д. Требуется определить давления в узловых точках газопровода. В соответствии с уравнением (5.2) и рис. 5.1 имеем:
и т. д. Требуется определить давления в узловых точках газопровода. В соответствии с уравнением (5.2) и рис. 5.1 имеем:
для первого участка  ;
;
для второго участка  ;
;
для  -го участка
-го участка  ;
;
для конечного  .
.
Сложив эти уравнения, получим
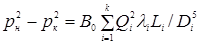
Давление в конце участка  может быть найдено из формулы
может быть найдено из формулы
 (5.5)
(5.5)
или
 (5.6)
(5.6)
в зависимости от того, какое давление известно –  или
или  .
.
Предварительно, разумеется, должны быть определены коэффициенты гидравлического сопротивления  . Это не вызовет затруднений, поскольку
. Это не вызовет затруднений, поскольку  и
и  известны. Если отборы (подкачки) невелики, то целесообразным оказывается трубопровод постоянного диаметра.
известны. Если отборы (подкачки) невелики, то целесообразным оказывается трубопровод постоянного диаметра.
Будем иметь
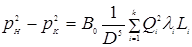
Приняв, что режим течения газа квадратичный и, следовательно, коэффициенты гидравлического сопротивления на всех участках одинаковы, получим
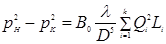
откуда легко определяется диаметр  , поскольку коэффициент гидравлического сопротивления
, поскольку коэффициент гидравлического сопротивления  есть функция диаметра. При необходимости можно воспользоваться формулой (5.5) или (5.6) и определить давления в узловых точках.
есть функция диаметра. При необходимости можно воспользоваться формулой (5.5) или (5.6) и определить давления в узловых точках.
V.II Способы приведения сложного газопровода к простому
Сложный газопровод может быть приведен к простому заменой его на эквивалентный или при помощи специальных коэффициентов.
Эквивалентным газопроводом называют однониточный постоянного диаметра, равноценный по пропускной способности рассчитываемому.
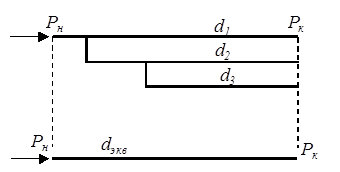
Рис. 5.2. Эквивалентный газопровод
Очевидно, что для любого газопровода можно подобрать целый ряд эквивалентных, различающихся по диаметру и длине. Их может быть столько, сколько существует значений внутренних диаметров труб, выпускаемых промышленностью. Чтобы задача была определенной, одна из указанных величин – либо диаметр, либо длина – должна быть задана. Вторая должна определяться специальным расчетом. Ясно, что эквивалентной может быть названа лишь эта вторая, т. е. подлежащая определению величина. Если считать заданной длину эквивалентного газопровода (естественно принять ее равной фактической длине  ), то пропускная способность рассчитываемого газопровода будет определяться формулой, аналогичной (5.3):
), то пропускная способность рассчитываемого газопровода будет определяться формулой, аналогичной (5.3):
 (5.7)
(5.7)
А если заданным считать диаметр эквивалентного газопровода D0 (произвольная величина), то
 (5.8)
(5.8)
В первом случае определению подлежит эквивалентный диаметр DЭ, а во втором – эквивалентная длина LЭ.
Привести сложный газопровод к эквивалентному – значит определить специальным расчетом либо  , либо
, либо  . Оба эти способа равноправны. Расчет состоит в том, чтобы выразить
. Оба эти способа равноправны. Расчет состоит в том, чтобы выразить  или
или  сложного газопровода через
сложного газопровода через  или
или  простых трубопроводов, входящих в его состав. Для простого трубопровода эквивалентный и фактический диаметры совпадают, т. е.
простых трубопроводов, входящих в его состав. Для простого трубопровода эквивалентный и фактический диаметры совпадают, т. е.  , а эквивалентная длина
, а эквивалентная длина  следует из сопоставления формул (5.7) и (5.8). Приведение сложного газопровода к эквивалентному при помощи
следует из сопоставления формул (5.7) и (5.8). Приведение сложного газопровода к эквивалентному при помощи  , как видно, несколько проще, чем при помощи
, как видно, несколько проще, чем при помощи  . Отдадим ему предпочтение.
. Отдадим ему предпочтение.
Теперь рассмотрим приведение сложного газопровода к простому при помощи специальных коэффициентов. Введем в рассуждение «эталонный газопровод» . Диаметр эталонного газопровода (обозначим его  ) – произвольная величина. Удобно принять
) – произвольная величина. Удобно принять  =1000 мм. Пропускная способность эталонного газопровода
=1000 мм. Пропускная способность эталонного газопровода
 (5.9)
(5.9)
Умножим и разделим правую часть (5.7) на  . Получим, что пропускная способность сложного газопровода
. Получим, что пропускная способность сложного газопровода
 (5.10)
(5.10)
Сомножитель  называется коэффициентом расхода газопровода:
называется коэффициентом расхода газопровода:  .
.
Из сопоставления (5.10) и (5.9) следует, что  , откуда и происходит название этого коэффициента.
, откуда и происходит название этого коэффициента.
Для простого трубопровода диаметром 
 , поскольку в этом случае, как уже было показано,
, поскольку в этом случае, как уже было показано,  .
.
При расчете сложных газопроводов, содержащих блоки с параллельными трубопроводами различной длины, весьма удобным оказывается коэффициент, включающий в себя не только эквивалентный диаметр  , но и длину газопровода
, но и длину газопровода  . Обозначим этот коэффициент
. Обозначим этот коэффициент  и назовем его «коэффициентом приведения».
и назовем его «коэффициентом приведения».
Формула пропускной способности теперь будет иметь вид
 (5.11)
(5.11)
Из формул (5.11), (5.10) и (5.7) следует связь  с
с  и
и  :
:
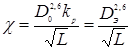
Как и  , коэффициенты
, коэффициенты  и
и  учитывают особенности конструкции рассчитываемого газопровода. Поэтому определение
учитывают особенности конструкции рассчитываемого газопровода. Поэтому определение  или
или  сложного газопровода, как и определение
сложного газопровода, как и определение  , означает приведение его (газопровода) к простому.
, означает приведение его (газопровода) к простому.
Итак, чтобы рассчитать сложный газопровод (вычислить  или
или  ), необходимо прежде всего определить
), необходимо прежде всего определить  или
или  или
или  этого газопровода.
этого газопровода.
В большинстве случаев сложный газопровод можно представить состоящим из отдельных блоков трубопроводов, соединенных друг с другом параллельно или последовательно. В свою очередь, каждый из этих блоков может состоять из более мелких блоков, соединенных тоже параллельно или последовательно вплоть до отдельных ниток. Рассмотрим, как определяются  ,
,  и
и  при параллельном и последовательном соединении трубопроводов (или блоков).
при параллельном и последовательном соединении трубопроводов (или блоков).
V.III Параллельные газопроводы
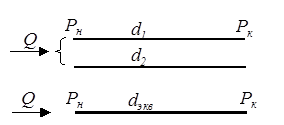
Рис. 5.3. Параллельное соединение газопроводов
Пропускная способность газопровода любой конструкции, в том числе и системы параллельных трубопроводов, как уже было показано, может быть выражена формулами (5.7), (5.10) или (5.11).
Пропускная способность  -го трубопровода, входящего в эту систему, qi выражается такими же формулами. Следует лишь
-го трубопровода, входящего в эту систему, qi выражается такими же формулами. Следует лишь  ,
,  или
или  приписать индекс
приписать индекс  . Учитывая, что
. Учитывая, что  , где
, где  – число параллельных трубопроводов, получаем
– число параллельных трубопроводов, получаем
Согласно уравнениям (5.7), (5.10), (5.11) 
 ,,
,,  ,
,  следует
следует
 ;
;  ;
;  . (5.12)
. (5.12)
Очевидно, что первые два равенства действительны лишь при условии, что  , т. е. все параллельные трубопроводы имеют одну и ту же длину. Последнее равенство свободно от этого ограничения; оно справедливо также и при неодинаковых длинах параллельных трубопроводов. В этом – некоторое преимущество приведения сложного газопровода к простому при помощи коэффициента
, т. е. все параллельные трубопроводы имеют одну и ту же длину. Последнее равенство свободно от этого ограничения; оно справедливо также и при неодинаковых длинах параллельных трубопроводов. В этом – некоторое преимущество приведения сложного газопровода к простому при помощи коэффициента  .
.
V.IV Последовательно соединенные газопроводы
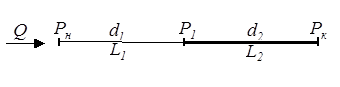
Рис. 5.4. Последовательное соединение газопроводов
Напишем формулы разности квадратов давления:
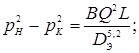
 и т.к.
и т.к. 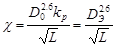
 (5.13)
(5.13)
Эти формулы пригодны для газопроводов любой конструкции, в том числе и для рассматриваемой.
Аналогично (5.13) напишем, чему равны разности квадратов давлений  для последовательно соединенных участков. Сложив эти равенства, будем иметь
для последовательно соединенных участков. Сложив эти равенства, будем иметь
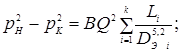
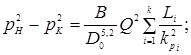
 (5.14)
(5.14)
Теперь сопоставим (5.37) и (5.38). Получим, что при последовательном соединении трубопроводов (или трубопроводных блоков)

 и
и  (5.15)
(5.15)
V.V Газопроводы, состоящие из параллельно и последовательно соединенных блоков
Процедура приведения таких газопроводов к простому или, что то же, определение их  ,
,  или
или  прежде всего состоит в том, чтобы выделить сначала самые крупные блоки, из которых состоит газопровод, затем более мелкие блоки и так далее до отдельных ниток. Помня, что при параллельном соединении складываются
прежде всего состоит в том, чтобы выделить сначала самые крупные блоки, из которых состоит газопровод, затем более мелкие блоки и так далее до отдельных ниток. Помня, что при параллельном соединении складываются  ,
,  или
или  , а при последовательном –
, а при последовательном –  ,
,  или
или  , составляются в той же последовательности выражения, определяющие эти параметры.
, составляются в той же последовательности выражения, определяющие эти параметры.
Следующий этап – определение численных значений  ,
,  или
или  отдельных трубопроводов (ниток) затем блоков и, наконец, всего газопровода.
отдельных трубопроводов (ниток) затем блоков и, наконец, всего газопровода.
Способы приведения сложного газопровода к простому при помощи  ,
,  или
или  , очевидно, равноценны. Однако при неодинаковых длинах параллельных трубопроводов в каком-либо блоке коэффициент
, очевидно, равноценны. Однако при неодинаковых длинах параллельных трубопроводов в каком-либо блоке коэффициент  оказывается предпочтительным.
оказывается предпочтительным.
V.VI Газопроводы с лупингами; увеличение пропускной способности газопроводов
Лупинги предназначаются либо для увеличения пропускной способности, либо для повышения давления в конечной точке газопровода, либо для снижения давления в начальной точке. Цель расчета – определение длины лупинга, при которой обеспечивается требуемый эффект. Газопровод с лупингом – один из простейших видов сложных газопроводов. При расчете газопроводов с лупингами удобно пользоваться коэффициентами расхода.
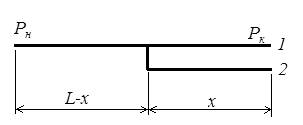
Рис 5.7. Схема газопровода с лупингом.
Определим коэффициент расхода газопровода, схема которого изображена на рис. 5.7. Газопровод состоит из участков  и
и  .
.
Первый из них – однониточный, диаметром  ; коэффициент расхода этого участка –
; коэффициент расхода этого участка –  .
.
Участок  – двухниточный; диаметры ниток –
– двухниточный; диаметры ниток –  и
и  , коэффициент расхода
, коэффициент расхода  .
.
Участки  и
и  соединены последовательно. Поэтому в соответствии с (5.15) будем иметь
соединены последовательно. Поэтому в соответствии с (5.15) будем иметь
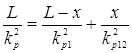
где  – коэффициент расхода всего газопровода; коэффициент расхода
– коэффициент расхода всего газопровода; коэффициент расхода  следует считать известной величиной; коэффициент расхода
следует считать известной величиной; коэффициент расхода  подлежит определению.
подлежит определению.
Поскольку трубопроводы 1 и 2 соединены параллельно, согласно (5.12)  (как и
(как и  , коэффициент
, коэффициент  – тоже известная величина). Получим
– тоже известная величина). Получим
 (*)
(*)
откуда
 (5.16)
(5.16)
Теперь сравним пропускную способность газопровода с лупингом ( ) с пропускной способностью газопровода без лупинга (
) с пропускной способностью газопровода без лупинга ( ). При условии, что давления
). При условии, что давления  и
и  до и после прокладки лупинга одинаковые, на основании формулы (5.10) можно написать, что коэффициент увеличения пропускной способности
до и после прокладки лупинга одинаковые, на основании формулы (5.10) можно написать, что коэффициент увеличения пропускной способности  . Учитывая (5.16), получим, что
. Учитывая (5.16), получим, что
 (5.17)
(5.17)
Из (5.17) находим, что длина лупинга, необходимая для увеличения пропускной способности в  раз,
раз,
 (5.18)
(5.18)
В частном случае, когда диаметры магистрали и лупинга D1 и D2 одинаковые, kp2 = kp1 и формулы (5.17) и (5.18) примут вид
 и
и  (5.19)
(5.19)
Теперь найдем длину лупинга, для случая, когда необходимо повысить давление рк до рк* (при неизменной пропускной способности Q).
Из уравнений
 – для газопровода без лупинга
– для газопровода без лупинга
 – для газопровода с лупингом
– для газопровода с лупингом
получим
 (5.20)
(5.20)
а при одинаковых диаметрах лупинга и магистрали (D2 = D1)
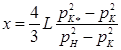
Если же лупинг прокладывается для снижения давления рH до рH*, то, поступив аналогично, найдем
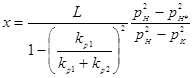
и при D2 = D1
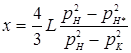
Второй способ увеличения пропускной способности газопровода – удвоение числа компрессорных станций. Считая, что это равносильно сокращению расстояний между станциями вдвое, напишем: до удвоения числа станций
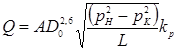
и после удвоения
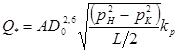
Отсюда следует, что коэффициент увеличения пропускной способности
 .
.
V.VII Многониточный газопровод с лупингом
Рассмотрим n-ниточный газопровод с лупингом.
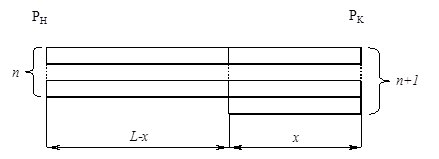
Рис. 5.8. Схема многониточного газопровода с лупингом.
Начальная точка лупинга соединена со всеми п трубопроводами (рис. 5.8). По-прежнему будем считать, что рассматриваемый газопровод состоит из двух последовательно соединенных блоков: L–х и х.
Блок L–х составлен из п, а блок х– из п + 1 параллельно идущих ниток.
Очевидно, что формулы для χ и для х будут иметь вид, аналогичный (5.17) и (5.18).
Достаточно лишь заменить в них kp1 на  и kp1 + kp2 на
и kp1 + kp2 на  .
.
Получим, что коэффициент увеличения пропускной способности при прокладке лупинга длиной х
 (5.21)
(5.21)
а длина лупинга при заданном значении χ
 (5.22)
(5.22)
Длина лупинга, необходимая для увеличения конечного давления рк до рK* согласно уравнению (5.20)
 (5.23)
(5.23)
Из трех последних формул видно: чем больше число ниток п, тем меньше эффективность лупинга – коэффициент увеличения пропускной способности χ уменьшается, длина лупинга, обеспечивающая заданные χ, или рк*, возрастает.
V.VIII Эффективность перемычек
Если лупинг соединен лишь с частью параллельных ниток (рис. 5.9) или лишь с одной из них, то линия падения квадратов давления у ниток, связанных с лупингом, будет с изломом (в точке подключения лупинга), а у «свободных» ниток – без излома.
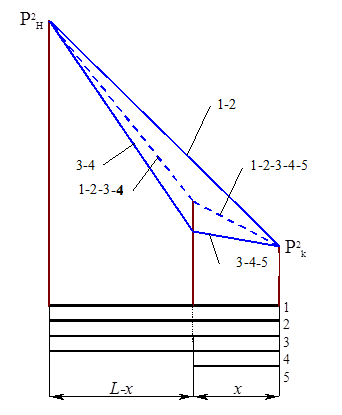
Рис. 5.9. Линии падения квадратов давлений :
1-2- в нитках 1 и 2, не соединённых перемычкой;
3-4- в нитках 4 и 3 на участке L-x ;
3-4-5- в нитках 3, 4 и 5 на участке х; 1-2-3-4 и 1-2-3-4-5 - в соответствующих нитках на участках L-x и х после соединения всех ниток.
Давление в свободных нитках будет выше, чем в лупингованных. Если теперь соединить перемычкой все нитки, то давления сравняются и линия падения квадратов давления будет для всех ниток одна и та же (на рис. 5.9 – пунктирная). Произойдет перераспределение расходов, в результате чего пропускная способность газопроводной системы увеличится.
Отношение пропускной способности газопровода с перемычкой к пропускной способности до включения перемычки будем называть эффективностью перемычки.
Перемычки эффективны не только в местах присоединения лупингов, но и в точках, где изменяются диаметры трубопроводов. В этих точках изменяется угол наклона линии падения квадрата давления, и соединение перемычкой таких ниток с другими приведет к перераспределению расходов и, следовательно, к увеличению пропускной способности.
Очевидно, что с увеличением числа ниток эффективность перемычки уменьшается. Очевидно также, что эффективность перемычки уменьшается с уменьшением различия в диаметрах участков. Если диаметры параллельных ниток не изменяются по длине и если отсутствует лупинг, то перемычки как средство, увеличивающее пропускную способность газопровода, оказываются бесполезными (в этом случае линия падения квадрата давления будет одна, общая для всех параллельных ниток). Однако это не означает, что для таких газопроводов перемычки не нужны. Перемычки позволяют, например, уменьшить снижение пропускной способности при аварийных или планово-предупредительных ремонтах трубопровода. Эти работы ведутся не на всей поврежденной нитке, а на сравнительно небольшой ее части. При помощи кранов ремонтируемый участок отключается. Пропускная способность газопровода при этом снижается. Очевидно, что чем меньше длина ремонтируемого участка и, следовательно, чем большее число перемычек имеет система трубопроводов, тем меньше будет снижение пропускной способности.
Определим число перемычек, при котором пропускная способность уменьшается до заданного предела. Обозначив длину ремонтируемого участка L–х, получим, что число перемычек
 (5.46)
(5.46)
Пусть общее число ниток газопровода равно п. Тогда при отключении на участке L–х одной нитки на ремонт газопровод можно считать n–1-ниточным с лупингом длиной х. Далее поступим аналогично тому, как это было при определении коэффициента увеличения пропускной способности п-ниточного газопровода прокладкой лупинга. Отличие состоит лишь в том, что сейчас требуется определить не коэффициент увеличения пропускной способности, а коэффициент ее уменьшения
ψ = Qn-1/Qn
где Qn-1 – расход при отключении участка L–х одной из ниток на ремонт;
Qn – расход, когда все нитки загружены полностью.
В результате будем иметь (анологично, как (5.21)):
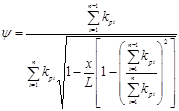
Лекция "Лекция 8" также может быть Вам полезна.
Отсюда находим относительную длину неремонтируемой части газопровода х/L и подставляем в (5.24). В результате получаем формулу, определяющую число перемычек в зависимости от заданного снижения пропускной способности:
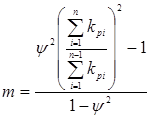
В частности, если число ниток n=2, то

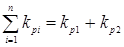
и формула числа перемычек будет выглядеть проще:
 .
.






















