ТЕМА 5. Функциональные сети
Тема 5. Лекция 6. Функциональные сети
- Понятие о детерминистских и стохастических сетях
- Характеристики символов, используемых в диаграммах
- Моделирование процесса с помощью сети GERT
1. Понятие о детерминистских и стохастических сетях
В последнее время для исследования происшествий в техносфере предлагается использовать диаграммы влияния, относящиеся к классу семантических функциональных сетей.
Семантические функциональные сети также являются графами, но отличаются дополнительной информацией, содержащейся в их узлах и дугах (ребрах).
Функциональные сети могут быть как стохастическими, так и детерминистскими.
Детерминистские сети, предусматривают необходимость реализации всех условий (дуг) для достижения конкретного события (узла). Пример детерминистской сети – сеть PERT.
Стохастические сети могут ограничиваться выполнением лишь части условий и событий, заданных предшествующими элементами. При этом выбор их проводится случайным образом, как правило, в соответствии с присвоенными элементам вероятностями или вероятностными распределениями.
Рекомендуемые материалы
Из них наиболее пригодны для исследования условий возникновения и предупреждения происшествий так называемые сети стохастической структуры типа Петри и GERT (Graphic Evaluation and Review Technique).
Достоинствами таких сетей являются:
а) возможность объединения логических и графических способов представления исследуемых событий;
б) учет стохастичности информации, выраженной узла ми и лугами;
в) доступность для моделирования параллельно протекающих, циклических и многократно наблюдаемых процессов;
г) наибольшие (по сравнению с другими типами диаграмм) логические возможности — в смысле строгости, компактности и простоты корректировки условий наблюдения моделируемых событий и явлений.
Отличительной особенностью функциональных сетей типа Петри и GERT служит не детерминистская (как PERT], а так называемая стохастическая структура. Это означает, что для завершения моделируемого ими процесса или появления интересующего исследователя события необходимо реализовать не все входящие дуги (предецессоры) и исходящие (саксессоры), а только ту их совокупность, которая минимально необходима и достаточна для этого. В тех случаях, когда соответствующий ресурс является переменной величиной, реализация конкретных дуг сети сопровождается выбором ее значения в соответствии с заданным им вероятностным распределением.
Стохастические сети, как и взвешенные и функциональные орграфы чувствительны к: динамике моделируемых процессов. Кроме того, они допускают возможность учета ряда дополнительных условий и ограничений, в том числе - связанных с цикличностью и наличием обратных связей. Все эти особенности сетевых, моделей позволяют отражать взаимодействие управляющих и управляемых элементов, декомпозировать сложные процессы до совокупностей простых, использовать их для определения количественных характеристик рассматриваемого процесса, уточнять состав необходимых для этого исходных данных и получать новую информацию о способах совершенствования безопасности, рассматривая ее как функциональное свойство человекомашинных систем.
|
Рис.1. Сеть Петри |
Отдельные элементы таких сетей могут не иметь физического смысла, а использоваться для указания логической последовательности реализации моделируемого процесса, т.е. соблюдения определенных отношений предшествования и завершения его этапов. Как следствие, стохастические сети часто содержат вспомогательные узлы и дуги.
Примером таких сетей могут служить сети GERT.
Функциональные сети GERT обладают стохастической структурой, что достигается присвоением узлам логических функций, а связям между ними – вероятности их реализации, активности или соблюдения другого условия (эти признаки характерны и для известного вам дерева отказов, но, как мы увидим дальше GERT – сети имеют специфические отличия).
Сети GERT имеют в общем случае четыре типа узлов (источник, сток, метка и статистика), каждая пара которых является ориентированной ветвью с определенным числом степеней свободы, что, собственно, и отличает их от графов и деревьев.
Как и в других диаграммах влияние, узлы изображаются специальными фигурами (см. табл.1).
2. Характеристики символов, используемых в диаграммах
Табл.
| Символ | Название | Назначение в модели |
| Состояние, свойство, событие | Обозначение существенных элементов объекта (процесса) | |
| Исходное или конечное событие («исток») | Элементы, не подлежащие дальнейшему анализу | |
| Знак «или» | Выход – при наличии любого из входных условий | |
| Знак «или» исключающее | Выход – при наличии одного (но не обоих) входов | |
| Знак «и» | Выход – при условии одно-временно всех входов | |
| Знак «и» приоритетное | Выход – только при определенном порядке входов | |
| Знак голосования | Выход при наличии любых m из n входов | |
| Стохастический вход и выход | Начало соблюдения условия с вероятностями Р1, Р2, Р3… | |
| Стохастический узел – разветвле-ние | Начальное и конечное условия с вероятностями Р1, Р2, Р3 | |
| - - - - - - | «Отношения» | Эпизодическое и логическое влияние |
| «Связь» | Постоянное одностороннее действие | |
| «Влияние» | Постоянное двустороннее взаимодействие | |
| Задержка | Выход при условии расхода ресурса (времени) i |
Число степеней свободы узла сети указывает на количество непосредственно ему предшествующих (инцидентных) условий, необходимых для его реализации.
Например, если число степеней свободы равно 2, а узлу предшествуют четыре условия, то для появления события (достижения узла) требуется соблюдение любых двух из них; при четырех степенях свободы необходимо выполнение всех четырех условий (число степеней свободы узла сети GERT может и превышать количество инцидентных ему связей; в этом случае предполагается многократность реализации отдельных условий: например, для четырехстепенного узла и одной связи потребуется ее четырехкратная реализация.
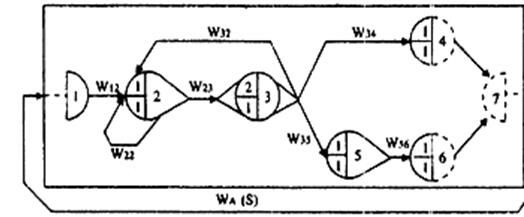
На рис. 2 показан пример простейшей сети GERT.
В этой сети шесть узлов и связей между ними.
Узел № 1 – исток (не имеет входных дуг).
Узлы № 2 и № 5 – детерминистские по входу и стохастические по выходу. Они имеют соответственно 2 и 1 инцидентные связи со степенями свободы, равными 1 для начальной (цифры «1» в левом верхнем секторе узлов) и последующих реализациях процесса.
Узлы №4 и № 6 – стоки (нет выходных дуг).
|
|
3. Моделирование процесса с помощью сети GERT
Моделируемый процесс протекает следующим образом.
Вначале реализуется связь 12, после чего осуществляется воздействие по одной из выходных дуг: 23 или 22 узла №2. После двух реализаций связи 23 открывается узел №3 и процесс может пойти по одному из трех возможных направлений.
Если реализуется условие 34, то он будет завершен, а, если 35, то реализуется событие 5 и, затем, после осуществления воздействия 56 – событие 6.
Если реализуется выход 32, процесс возобновится с момента осуществления связей 23 и 22, однако его предыстория будет зафиксирована узлами – метками №2, №3 и №5 и узлами-стоками №4 и №6.
Для определения вероятности наступления конкретного события сети - Q, математического ожидания - M[Т] и дисперсии времени до его появления – D[T]), обычно проводят упрощение исходной модели, путем объединения последовательных, параллельных и замкнутых контуров единственную ветвь с эквивалентными исходными параметрами Pij, Mij (S) и их преобразованием Wij(S). Значение функции Wij(S), иногда называемой коэффициентом пропускания или оператором динамической системы [22], рассчитывается с соблюдением следующих правил[105]:
а) для последовательно соединенных узлов i, j, k:
Wik*(k)=Wij(S)×Wjk(S) (1)
б) для параллельных ветвей между узлами 1-2 и 3-4, условно объединенных в один главный исток под номером i = (1 Ç 3) и один главный сток k = (2 Ç 4).
Wik*(k)=W12(S)×W34(S) (2)
в) для сочетания одной дуги i-k с собственной (вырожденной, первого порядка) петлей i-I
 (3)
(3)
г) для петли т-го порядка - множества из т не связанных между собой замкнутых ветвей первого порядка
 (4)
(4)
Заметим, что правила преобразования сетей, помеченные буквами (а...г), справедливы лишь для так называемых замкнутых стохастических связей, т.е. таких, для которых существует обратная связь между главным или каким-то другим стоком и главным истоком. В тех же случаях, когда рассматриваются разомкнутые функциональные сети стохастической структуры, такие, например, как приведенная выше, для использования этих правил необходимо проводить их искусственное замыкание дугой с подобранным специальным образом коэффициентом пропускания WA(S).
Процедура такой модификации исходной сети и определения значения ее функции WE(s) основана на использовании топологического уравнения С.Мэсона[105, 109], имеющего следующий вид:
 (5)
(5)
где  - сумма коэффициентов пропускания i-ых петель сети.
- сумма коэффициентов пропускания i-ых петель сети.
Последовательность определения функции WE(S) для разомкнутой (оригинальной) стохастической сети по формуле (5), с учетом вышеизложенного включает такие основные шаги:
1. Замыкание главного или другого стока конкретной сети - одного из возможных исходов рассматриваемого процесса с главным ее истоком (начальным событием) и присвоение этой обратной связи коэффициента пропускания WA(S).
2. Определение значения искомого коэффициента пропускания разомкнутой стохастической сети - WE(S) с помощью аналогичного параметра ранее введенной обратной связи - WA(S) и формул (4), (5).
3. Выявление всех возможных (включая и введенную искусственно связь) петель и вычисление их эквивалентных коэффициентов пропускания – W*(Li).
4. Подстановка значений W*(Li) и WE(S) =f[WA(S)] в топологическое уравнение (5), уточнение знаков слагаемых и разрешение его относительно искомой нами функции WE(S).
Если Вам понравилась эта лекция, то понравится и эта - 5. Профессиональные системы и технологии.
Проиллюстрируем рассмотренный порядок анализа стохастических сетей для случая определения таких характеристик, как математическое ожидание и дисперсия величины, например, времени, необходимого для реализации конкретного исхода, а также вероятность его возникновения. В качестве модели рассмотрим уже знакомую сеть типа GERT (см. рис. 2), а затем исследуем процесс возникновения конкретного транспортного происшествия - железнодорожного крушения.
Очевидно, что рассматриваемые процессы могут интерпретироваться в виде прохождения сигнала по узлам и дугам соответствующей сети. имеющей в своем составе последовательные, параллельные, а иногда и замкнутые сочетания ориентированных ветвей. Следовательно, вероятность появления интересующих нас исходов, а также математическое ожидание величины времени до их возникновения - М[Т] и его дисперсия D[T] будут зависеть от структуры сети и пропускных способностей ее элементов, характеризуемых параметрами tij и Pij или однозначно связанной с ними функцией.
|
Рис. 3. Модифицированная сеть GERT |
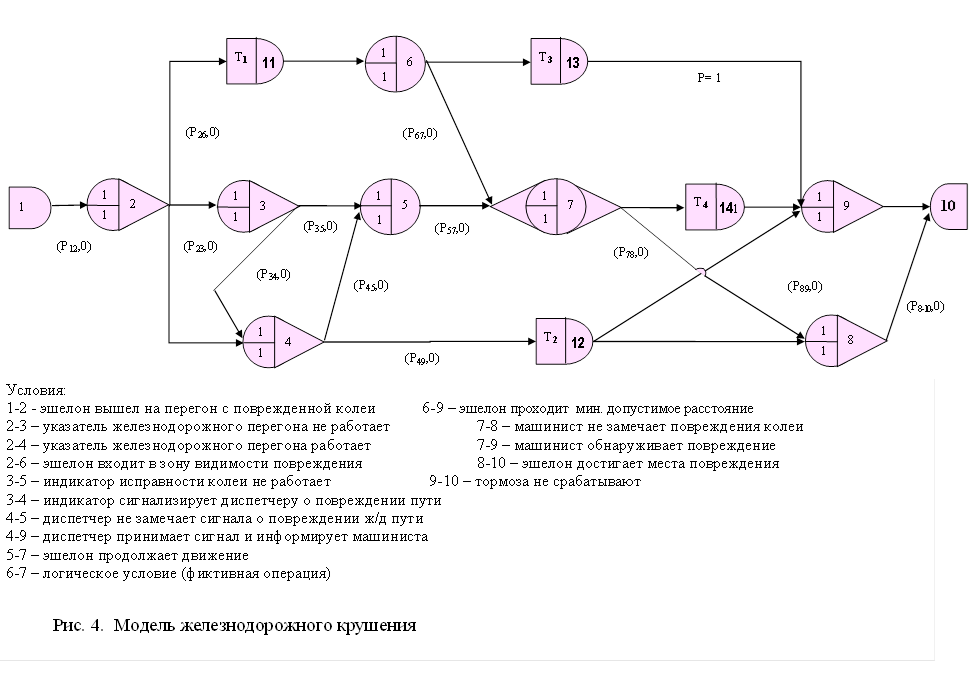



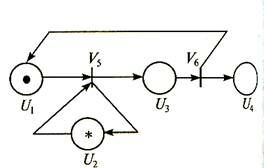
 Рис. 2. Стохастическая сеть GERT
Рис. 2. Стохастическая сеть GERT