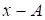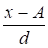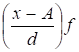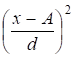Показатели вариации
Тема 6. Показатели вариации
6.1. Понятие вариации признака и значение ее статистического изучения
Вариацией признака называется наличие различий в численных значениях какого-либо признака внутри совокупности. Причиной колеблемости признаков является множественность действующих факторов. Среди значительного числа факторов всегда найдется один или несколько, которые не останутся постоянными, что неизбежно скажется на общем итоге их влияния, а следовательно, и на признаках изучаемых явлений.
Показатели вариации изучаются для решения вполне определенных задач, одной из которых является оценка типичности средней величины.
Как известно, средняя величина лишь в том случае может считаться инструментом научного исследования, когда она исчислена для однокачественных единиц. В противном случае она является огульной средней и непригодной для статистического анализа. Оценка типичности средней – это и оценка однородности совокупности, для которой она исчислена. Представление об отклонении индивидуальных значений от средней и дают показатели вариации.
Средняя представляет вариационный ряд в целом, не показывая, как располагаются около нее отдельные варианты, сконцентрированы ли они вблизи нее или значительно отклоняются от нее.
6.2. Показатели вариации
Вариацию можно количественно характеризовать несколькими показателями. Самое первое представление о степени колеблемости значений совокупности дает размах вариации.
Размах вариации  – это амплитуда колебания, определяется как разность между экстремальными значениями вариационного ряда
– это амплитуда колебания, определяется как разность между экстремальными значениями вариационного ряда  . Размах вариации является величиной неустойчивой и не может в полной мере охарактеризовать колеблемость ряда по двум причинам:
. Размах вариации является величиной неустойчивой и не может в полной мере охарактеризовать колеблемость ряда по двум причинам:
1) не учитывает промежуточных значений вариант внутри крайних пределов, а поэтому не отражает колеблемость ряда в целом;
2) основываясь только на двух значениях, которые могут оказаться недостаточно характерными, может отражать случайную, а не типичную для данного ряда величину колеблемости.
Вариационный размах имеет и самостоятельное значение. Например, в промышленности допуски точности изготовляемых изделий устанавливаются в определенных пределах, что соответствует величине размаха вариации их признаков. В судоходстве показатели крайних значений глубины судоходных путей являются предельной границей для пропуска судов с соответствующими осадками.
Рекомендуемые материалы
Последующие показатели вариации являются логическим следствием поиска устранения недостатков размаха вариации и более точной характеристики колеблемости признаков по сравнению с типическим уровнем – со средней величиной, как эталоном.
Стремление ослабить влияние случайных факторов приводит к расчету среднего линейного отклонения. Это отклонение определяется как средняя арифметическая из абсолютных значений отклонений индивидуальных значений признака от средней величины. Для сгруппированных данных расчет ведется по формуле:
 .
.
Для несгруппированных данных применяется формула:
 .
.
При расчете среднего линейного отклонения во внимание принимаются все без исключения элементы ряда. Однако это улучшение достигается посредством нарушения элементарных правил математики (отбрасываются знаки, т.к. сумма отклонений индивидуальных значений от средней равна нулю).
Широкое распространение получил показатель дисперсия – средняя величина из квадратов отклонений от средней  , расчет ее производится по ниже приведенным формулам соответственно для сгруппированных
, расчет ее производится по ниже приведенным формулам соответственно для сгруппированных
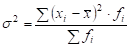
и несгруппированных данных:
 .
.
Дисперсия широко применяется в разного рода расчетах. Однако она не совсем удобна, т.е. является величиной неименованной в отличии от средней величины, что препятствует их сравнению. Чтобы устранить это препятствие из дисперсии извлекают квадратный корень и получают среднее квадратическое отклонение  :
:
 .
.
Среднее квадратическое отклонение используется для сопоставления вариации признака по нескольким однородным совокупностям или одной совокупности за разные годы. Например, исчисленная средняя себестоимость единицы продукции объединения в отчетном году по сравнению с прошлым годом снизилась, а среднее квадратическое отклонение возросло. Это говорит о том, что снижение средней себестоимости нельзя считать удовлетворительным, т.к. имеются существенные различия в себестоимости продукции передовых и отстающих предприятий данного объединения.
Среднее квадратическое отклонение является мерилом надежности средней. Чем ниже среднее квадратическое отклонение, тем типичнее средняя величина.
Среднее квадратическое отклонение является величиной именованной, поэтому его нельзя использовать в целях сопоставимости вариации средней выработки и средней заработной платы рабочих предприятия. Для достижения сопоставимости показателей вариации принято исчислять коэффициент вариации  :
:
 .
.
Т.е. коэффициент вариации – это процентное отношение среднего квадратического отклонения к средней величине.
Данный показатель применяется и тогда, когда дается сравнительная характеристика колеблемости одного и того же признака у разных совокупностей, например, сравнение размеров колеблемости урожайности различных культур, уровней производительности труда рабочих, занятых производством различных видов продукции.
Критическое значение коэффициента вариации – 35%. Совокупность можно считать более или менее однородной, а среднюю – типичной, если коэффициент вариации не более 35%. Если же коэффициент вариации равен или более 35%, то совокупность неоднородна, а средняя является огульной.
Рассмотрим пример расчета показателей вариации.
Урожайность пшеницы характеризуется следующими данными:
Таблица 6.1
| Урожайность | Посевная площадь, га | Середина интервала |
| 14-16 | 100 | 15 |
| 16-18 | 300 | 17 |
| 18-20 | 400 | 19 |
| 20-22 | 200 | 21 |
| Итого | 1000 | Х |
Определим: 1) среднюю урожайность:
 ц;
ц;
2) размах вариации:
 ц;
ц;
3) среднее линейное отклонение:
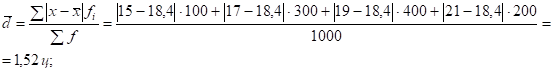
4) дисперсию:
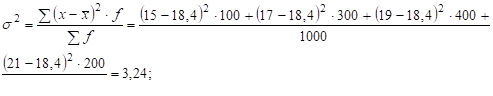
5) среднее квадратическое отклонение:
 ц;
ц;
6) коэффициент вариации:
 .
.
Таким образом, индивидуальная урожайность на отдельных участках колеблется от средней урожайности в среднем на  1,8 ц или
1,8 ц или  9,8%.
9,8%.
Между показателями вариации имеются определенные соотношения, знание которых позволяет переходить от одного показателя колеблемости к другому, не затрачивая существенных усилий на расчеты. Такой переход бывает необходим при решении ряда практических задач. Например, при некоторых способах статистического контроля устойчивости производственного процесса такие переходы от одного показателя к другому могут быть полезны.
Зная соотношение между различными показателями вариации можно находить приблизительную величину сложно исчисляемых показателей более просто, например, величину среднего квадратического отклонения исходя из размаха вариации:
 .
.
Соотношение между другими показателями вариации таково:
 точнее
точнее 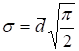
или
 точнее
точнее  .
.
Данные соотношения будут тем точнее, чем больше объем совокупности, а распределение ее ближе к нормальному.
6.3. Дисперсия альтернативного признака
В экономико-статистических исследованиях приходится встречаться с альтернативной изменчивостью качественных признаков. При альтернативной вариации имеются лишь два исключающих друг друга случая – наличие или отсутствие признака у единиц совокупности. Такими признаками, например, будут ученая степень у преподавателей вузов, диплом с отличием у выпускников института, наличие брака у изделий и т.д. Признаки, которыми обладают одни единицы совокупности и не обладают другие, называются альтернативными. Вариация этих признаков принимает два значения: имеется признак – 1, не имеется признака – 0. Доля единиц, обладающих данным признаком обозначается буквой  , не обладающих данным признаком –
, не обладающих данным признаком –  .
.
Применяя ранее рассмотренные формулы расчета можно определить среднюю и дисперсию альтернативного признака.
Исчислим:
1) среднее значение альтернативного признака:
 .
.
2) дисперсию альтернативного признака:
 Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, на долю единиц, не обладающих им.
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, на долю единиц, не обладающих им.
Пример: из 40 рабочих – 16 человек имеют среднее образование. Определить вариацию доли рабочих, имеющих среднее образование.
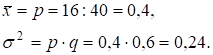
Максимальная величина дисперсии альтернативного признака 0,25.
Расчет дисперсии альтернативного признака применяется в выборочном наблюдении.
6.4. Упрощенные способы расчета дисперсии
Расчет дисперсии обычным способом (по формуле  ) часто бывает трудоемким. Для упрощения вычислений применяется ряд способов.
) часто бывает трудоемким. Для упрощения вычислений применяется ряд способов.
В тех случаях, когда варианты выражаются небольшими и немногозначными числами, дисперсия может быть найдена как разность между средним квадратом и квадратом средней величины:
 ,
,
где  , а
, а  .
.
Например, на станках-автоматах отработано 600 деталей, причем на каждую деталь затрачивалось 0,3 часа, а на обычных станках отработано 400 деталей при трудоемкости одной 1 час. Найдем дисперсию затрат труда на одну деталь:
 часа,
часа,
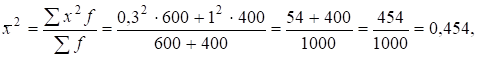
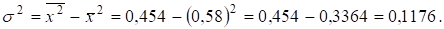
Дисперсию также, можно рассчитать способом моментов, который основан на нижеследующих математических свойствах дисперсии.
1. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не измениться.
2. Если все значения вариант разделить на какое-то постоянное число d, то дисперсия уменьшиться от этого в  раз.
раз.
Дисперсия способом моментов равна:
 ,
,
где  .
.
Расчет дисперсии способом моментов:
Таблица 6.2
| Группы рабочих по уровню выработки | Число рабочих | Середина интервала |
|
|
|
|
|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| до 1250 | 12 | 1 125 | -500 | -2 | -24 | 4 | 48 |
| 1250-1500 | 32 | 1 375 | -250 | -1 | -32 | 1 | 32 |
| Продолжение табл. 6.2 | |||||||
| 1500-1750 | 156 | 1 625 | 0 | 0 | 0 | 0 | 0 |
| 1750-2000 | 81 | 1 875 | 250 | +1 | 81 | 1 | 81 |
| 2000 и более | 119 | 2 125 | 500 | +2 | 238 | 4 | 476 |
| Итого | 400 | Х | 0 | 0 | 263 | 637 |
Сначала находим первый и второй моменты. Исходные данные для установления их величины в табл. 6.2 (в качестве А взяли центральную варианту 1625,  у нас равно 250).
у нас равно 250).
Отсюда:
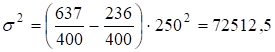
6.5. Виды дисперсий и правило их сложения
Разделив изучаемую совокупность на качественно однородные группы, можно исчислить для каждой из групп среднюю и дисперсию.
Групповая средняя говорит о среднем размере изучаемого признака данной группы единиц.
Групповая дисперсия характеризует средний квадрат отклонения индивидуальных значений данного признака от групповой средней.
Рассчитаем эти показатели по следующим данным:
Таблица 6.3
Урожайность картофеля по участкам
| Урожайность, в ц с 1 га | Участки, га | ||
| Всего | в том числе | ||
| удобренные | неудобренные | ||
| до 100 | 280 | – | 280 |
| 100-120 | 150 | 80 | 79 |
| 120-140 | 170 | 120 | 50 |
| 140 и выше | 400 | 400 | – |
| Итого | 1000 | 600 | 400 |
Определим групповые средние  по формуле:
по формуле:
 ,
,
где  – численность вариант в каждой группе.
– численность вариант в каждой группе.
Средняя урожайность картофеля на удобренных участках:
 ц.
ц.
Средняя урожайность на неудобренных участках:
 ц.
ц.
Исчислим групповые дисперсии:
 .
.
Дисперсия урожайности на удобренных участках:
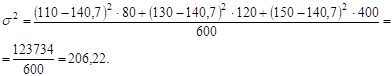
Дисперсия урожайности на неудобренных участках:
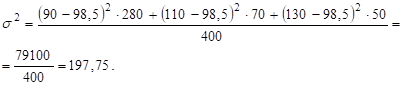
Можно рассматривать всю совокупность как единое целое, не подразделяя ее на группы и тоже исчислить общую среднюю и общую дисперсию.
Общая средняя характеризует средний размер признака в данной совокупности в целом.
Общая дисперсия показывает средний квадрат отклонений индивидуальных значений от общей (генеральной) средней.
Рассчитаем общую среднюю по формуле:
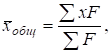
где  – численность всей совокупности.
– численность всей совокупности.
 ц.
ц.
Общая дисперсия:
 .
.
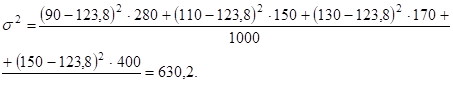
Между групповой и общей средней можно исчислить показатель вариации, где групповые средние рассматриваются как индивидуальные значения совокупности, это межгрупповая дисперсия:
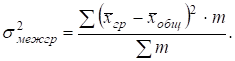
Межгрупповая дисперсия служит мерой колеблемости частных (групповых) средних около общей средней. Величина межгрупповой дисперсии указывает насколько частные совокупности однороднее общей.
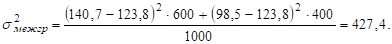
Таким образом получается три вида дисперсий: общая, групповая и межгрупповая. Все эти дисперсии взаимосвязаны между собой следующим образом: величина общей дисперсии равна сумме межгрупповой дисперсии и средней дисперсии из групповых.
Средняя дисперсия из групповых вычисляется как средняя взвешенная величина, в качестве веса берется численность каждой группы ( ):
):
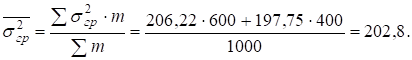
Бесплатная лекция: "Ограниченная протяженность во времени" также доступна.
Проверим взаимосвязь дисперсий, которую в математике называют теоремой или правилом сложения дисперсий:
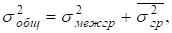
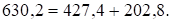
Общая дисперсия отражает вариацию результативного признака, вызванную воздействием всей совокупности факторов. В нашем примере она показывает вариацию урожайности на всем массиве под влиянием всех совместно действующих факторов: внесения удобрений, погодных условий, организации работ и т.д.
Межгрупповая дисперсия характеризует вариацию результативного признака, которая происходит под влиянием фактора положенного в основу группировки. Она характеризует колеблемость урожайности под влиянием одного фактора – внесенных удобрений.
Внутригрупповая дисперсия характеризует случайную вариацию. Эта вариация возникает под влиянием других, неучитываемых факторов и не зависит от признака – фактора, положенного в основу группировки.