Развитие математических моделей поршневых компрессоров
1.5. Развитие математических моделей поршневых компрессоров
Цель настоящего параграфа краткое рассмотрение истории математических моделей поршневых компрессоров и путей развития их в дальнейшем.
Математическая модель рабочего процесса. Первая математическая модель реального процесса, протекающего в поршневом компрессоре, и моделирование этого процесса были осуществлены до 1940г. в СССР Н.А.Доллежалем*, который исследовал процесс всасывания. В зарубежной литературе приоритет математического моделирования процесса всасывания и нагнетания в компрессорах с самодействующими клапанами иногда неверно отдается М. Костаглиоле. Результаты выполненной М. Костаглиолой в Массачусетском технологическом институте на эту тему были опубликованы только в 1950 г.** всех основных положений работ Н. А. Доллежаля и М. Костагли-олы была показана в специальной статье, посвященной этому вопросу.
Использование механических и электромеханических счетных машин. Как Н.А.Доллежаль, так и М. Костаглиола все расчеты, связанные с моделированием процессов всасывания и нагнетания в поршневом компрессоре, выполняли графически. В 1953 г. профессор Дж. Макларен (Шотландия) предложил математическую модель самодействующего клапана и процессов нагнетания, специально предназначенную для реализации на механической или электрической вычислительной машине.
Использование механических и электромеханических решения уравнений, моделирующих процессы всасывания и нагнетания, было известно в это время и в СССР. публикаций о специально выполненных для этой цели математических моделях не было.
Применение электронных вычислительных машин. важнейший этап развития математического моделирования поршневых компрессоров был связан с появлением вычислительной техники (АВМ и ЭЦВМ).
Пионерами в деле применения ЭЦВМ для моделирования рабочих процессов поршневых компрессоров признаны А. И. Борисоглебский и Р. В. Кузьмин*, которые, объединив уравнение расхода и уравнение изменения объема рабочей полости цилиндра с уравнением движения пластины клапана, получили обобщенное нелинейное уравнение третьего порядка и решили его на ЭЦВМ методом Рунге—Кутта. Применение ЭВМ позволило А. И. Борисоглебскому и Р. В. Кузьмину использовать зависимости, описывающие работу клапанов в функции 21 параметра. Отметим, что приблизительно в это же время работа самодействующих клапанов моделировалась на АВМ. Первые публикации об использовании ЭВМ для моделирования рабочих процессов поршневых компрессоров за рубежом были сделаны одновременно рядом авторов в 1967 г. (Р. Коэн, М. Уамбсгангс, Дж. Макларен, С. Керр, С. Тоубер).
Применение АВМ для моделирования рабочих процессов в поршневых компрессорах впервые было осуществлено в Ленинградском политехническом институте (1965—1966 гг.).
Приоритет применения гибридных ЭВМ для моделирования рабочих процессов в поршневых компрессорах принадлежит доктору С. Тоуберу из Делфтского технического университета (Голландия).
Рекомендуемые материалы
Моделирование полного рабочего цикла. Первая математическая модель полного рабочего цикла поршневого компрессора с реальными самодействующими клапанами была разработана М. Уамбсгангсом и Р. Коэном в Пардью университете (США) в 1966 г. Процессы всасывания и нагнетания в этой модели описывались на базе работы М. Костаглиолы в предположении о постоянстве давления во всасывающей и нагнетательной полостях, а процессы сжатия и расширения — политропными зависимостями. В результате были успешно смоделированы индикаторная диаграмма и диаграммы движения пластин всасывающих и нагнетательных клапанов малого холодильного компрессора.
Разработаны и успешно применяются математические модели рабочих процессов поршневых компрессоров с впрыском жидкости в рабочую полость цилиндра с целью охлаждения сжимаемого газа и уплотнения зазоров.
В настоящее время моделирование индикаторных диаграмм и диаграмм движения пластин самодействующих клапанов проводят практически при разработке каждого нового компрессора.
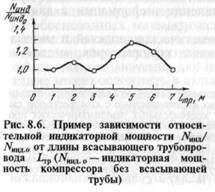
 Моделирование системы компрессор — трубопроводы. Еще в 1939 г. русский ученый А. Зеле-нов (МВТУ) установил влияние пульсаций потока газа во всасывающей системе на характеристики компрессора. Пульсации потока во всасывающих и нагнетательных трубопроводах, вызванные периодическими процессами всасывания и нагнетания, обусловливают изменения давления в полостях всасывания и нагнетания. Последние влияют на работу клапанов, а также на производительность и потребляемую мощность компрессора. На рис. 8.5 показаны диаграммы движения нагнетательного клапана в одном и том же компрессоре с нагнетательным трубопроводом различной длины, а на рис. 8.6 представлена зависимость относительной индикаторной мощности поршневого компрессора от длины всасывающего трубопровода (за единицу принята индикаторная мощность при отсутствии всасывающего трубопровода).
Моделирование системы компрессор — трубопроводы. Еще в 1939 г. русский ученый А. Зеле-нов (МВТУ) установил влияние пульсаций потока газа во всасывающей системе на характеристики компрессора. Пульсации потока во всасывающих и нагнетательных трубопроводах, вызванные периодическими процессами всасывания и нагнетания, обусловливают изменения давления в полостях всасывания и нагнетания. Последние влияют на работу клапанов, а также на производительность и потребляемую мощность компрессора. На рис. 8.5 показаны диаграммы движения нагнетательного клапана в одном и том же компрессоре с нагнетательным трубопроводом различной длины, а на рис. 8.6 представлена зависимость относительной индикаторной мощности поршневого компрессора от длины всасывающего трубопровода (за единицу принята индикаторная мощность при отсутствии всасывающего трубопровода).
Первую математическую модель поршневого компрессора с системой трубопроводов в 1969г. разработал чешский ученый И. Браблик. Он объединил модель работы клапана, разработанную М. И. Френкелем (см. главу 6), с описанием процессов пульсации потока в трубопроводах, используя концепцию волн малой амплитуды, и изучал совместную работу самодействующих клапанов и трубопроводов. По мнению специалистов, И. Браб-лику принадлежит также первенство в изучении сложных явлений пульсаций в трубопроводах по частям: он предполагал отсутствие пульсаций в нагнетательном трубопроводе, когда изучал
|
|
взаимодействие всасывающего трубопровода с всасывающими клапанами и их влияние на характеристики компрессора, и, наоборот, полагал отсутствие пульсаций на всасывании при изучении этих явлений на стороне нагнетания.
В дальнейшем было разработано несколько моделей поршневых компрессоров с нагнетательными и всасывающими трубопроводами с использованием метода неустановившихся течений с амплитудой колебания давлений конечной величины.
Математические модели, рассматривающие в комплексе все рабочие процессы в цилиндре, в полостях всасывания и нагнетания, работу клапанов, неустановившиеся потоки газа во всасывающих и нагнетательных трубопроводах, весьма сложны, требуют большого машинного времени, т. е. времени ЭВМ, большой памяти ЭВМ. Поэтому появились работы, направленные на уменьшение времени обсчета моделей, на увеличение точности моделей, на уточнение граничных условий.
В настоящее время математические модели и математическое моделирование широко применяют при разработке и исследовании новых машин.
Пути развития моделирования компрессоров. Развитие математического моделирования поршневых компрессоров идет в нескольких направлениях.
1. Создание и разработка концептуальных и методологическихоснов, разработка основных принципов построения математических моделей с целью их совместимости, разработка иерархии математических моделей.
2. Расширение применения математических моделей и математического моделирования, т. е. разработка задач нового типа, в которых использование математического моделирования может дать существенный эффект (задачи идентификации — оценки ненаблюдаемых параметров и ранжирования, задачи оптимизации, задачи автоматизированного проектирования и т. д.).
3. Совершенствование формального описания компрессоров,их элементов и протекающих в них процессов.
4. Получение новых экспериментальных данных, позволяющихуточнить математические модели, коэффициенты, в них содержащиеся, и граничные условия.
5. Разработка и совершенствование методов реализации математического моделирования (разработка новых, более точных илиболее экономичных вычислительных методов, обоснование применения новых методов представления информации в диалоге ЭВМ — человек).
Быстрое распространение математических моделей и математического моделирования поршневых компрессоров, «мода» на математические модели имеют свои отрицательные стороны, которые представляют определенные опасности для развития всего этого направления исследований в дальнейшем.
Первая опасность — загромождение науки большим количеством математических моделей, которые трудно объединить, результаты исследований на которых невозможно обобщить. Большая часть этих моделей полезна для накопления знаний и уточнения понимания отдельных деталей, относящихся к узким и частным вопросам, прежде всего проектирования. В настоящее время назревает необходимость во взаимной увязке, объединении результатов исследований, полученных математическим моделированием поршневых компрессоров, в более широкие многоаспектные концепции проектирования.
Необходимость совместимости, объединения и интеграции моделей обусловлена также разработкой автоматизированных систем по построению математических моделей поршневых компрессоров и систем с поршневыми компрессорами и разработкой общеотраслевой САПР поршневых компрессоров.
Вторая опасность заключается в том, что вокруг математического моделирования компрессоров возникают ненужная теоретизация, наукообразие. Появляются работы, которые на первый взгляд носят практический характер, но возникают лишь потому, что они представляют собой интересную математическую или вычислительную задачу. Такие работы требуют определенного математического мастерства, но в действительности не имеют никакого прикладного значения. С точки зрения вычислительной математики эти работы также не представляют интереса, зато, как кажется авторам, повышают престиж разработчиков. Появление таких «престижных» работ приводит к тому, что получение экспериментальных данных, действительно очень нужных для разработки математических моделей поршневых компрессоров, становится непрестижным и начинает казаться как бы второстепенной, второсортной работой.
Третья опасность состоит в том, что появление большого числа отличающихся друг от друга незначительными деталями или плохо обоснованных математических моделей компрессоров и их процессов в сочетании с математическими моделями, носящими «престижный» характер, не дает тех результатов, которые имеют действительное значение для науки и производства. Такое положение может осложнить в дальнейшем развитие математического моделирования компрессоров и вызвать трудности в расширении применения на практике этого эффективного метода исследования и расчета компрессорных машин.
Четвертая опасность — «слепая» вера в могущество метода математического моделирования, делающая его в глазах разработчиков математических моделей единственным правильным методом исследования. Такая точка зрения неверна, опасна, ибо общая концепция вычислительного эксперимента, т. е, математического моделирования, ни в коем случае не отвергает эксперимента на натурных машинах, а лишь дополняет его.
О модульном (блочном) математическом моделировании компрессоров. В настоящее время создание и совершенствование поршневых компрессоров без использования математических моделей невозможно. Разработано большое количество математических моделей, предназначенных для решения конкретных задач при проектировании, доводке и эксплуатации поршневых компрессоров.
Естественно, заманчивым и перспективным является создание библиотек таких математических моделей, с тем чтобы их можно было повторно использовать. Было предпринято несколько попыток создания подобных библиотек, которые не привели к положительному результату.
Стало очевидным, что создание библиотек математических моделей и их модулей требует принципиально нового подхода к разработке их структур. В МГТУ им. Н. Э. Баумана разработана система математического моделирования объемных компрессоров с использованием изменяемых структур и многовариантных модулей. К такой системе структур математических моделей и составляющих модулей предъявляются требования гибкости, для того чтобы она отразила все многообразие математических моделей рабочих процессов объемных компрессоров, и в то же время определенные требования на построение модулей, с тем чтобы они могли использоваться в данной системе (т. е. для того, чтобы все модули системы были совместимыми).
В МГТУ им. Н. Э. Баумана создана система математического моделирования (СММ) рабочих процессов поршневых компрессоров, соответствующая вышесформулированной цели. Разработанная СММ учитывает особенности вычислительного эксперимента как метода исследования рабочих процессов поршневых компрессоров, в том числе многократную изменяемость структур и модулей математических моделей. Эта система соответствует требованиям безболезненности изменений структур и составляющих модулей. Изменения программного продукта называют безболезненными, если они не нарушают работоспособность отлаженных ранее версий программы, сопроводительной документации и других подобных материалов (так называемая безболезненность для работоспособности). Существует также требование обеспечения безболезненности для окружения, при которой изменения содержимого программного продукта не приводят к необходимости изменения существовавших ранее текстов программ и других первичных материалов.
В разработанной СММ ключевыми являются понятия модуля и каркаса. Под модулем понимают элемент системы, в котором определяют только одну физическую величину. В общем случае лю
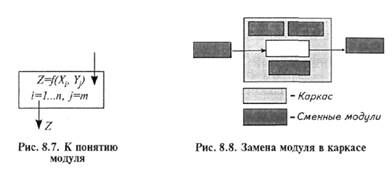
бой модуль в системе может быть схематизирован следующим образом (рис. 8.7):
У = (Y1 , Y2,..., Ym) — вектор входных параметров, вычисляемых в других модулях;
Х = (Х1, Х2, ..Хп) —вектор коэффициентов, задаваемых при расчете;
Z— рассчитываемая в модуле физическая величина.
Каркас — это структура, определяющая связи между вариантными гнездами, заполняемыми модулями, и реализующая эти связи при проведении вычислительного эксперимента. При этом можно изменить содержание одного или нескольких вариантных гнезд при сохранении обшей структуры программы (например, применить другую зависимость, определяющую вычисляемую величину). Тогда из вариантного гнезда «вынимают» один модуль, а на его место «устанавливают» другой (рис. 8.8).
Заполненный модулями каркас сам может служить модулем, используемым в каркасе более высокого уровня. И наоборот модуль может быть каркасом для модулей более низкого уровня (рис. 8.9).
Ещё посмотрите лекцию "Воздействие промывочной жидкости на продуктивный пласт" по этой теме.
Такой подход к построению моделирующей системы позволяет определить требования к разработке модулей и каркасов. Созданное в соответствии с этими требованиями множество модулей и каркасов представляет собой упорядоченную структуру — аналог библиотек программ. Структура модулей и каркасов не зависит от того, на каком языке программирования они будут написаны.
В системе математического моделирования наряду с библиотекой модулей созданы библиотека ведущих частей программ, т. е. каркасов, и библиотека вычислительных алгоритмов. При этом становится возможным использование готовых каркасов для заполнения их вариантных гнезд готовыми модулями из библиотек системы или вновь написанными модулями для сборки расчетного алгоритма конкретной конфигурации. Таким образом, один и тот же каркас можно использовать для разных целей и его не надо будет создавать каждый раз заново.
Предусмотрено, что сборка программы для создания и расчета конкретной математической модели будет осуществляться посредством диалога пользователя с так называемым конфигуратором программ, во время которого пользователь задает исходные данные для расчета, а конфигуратор осуществляет отбор необходимых модулей и каркасов с учетом их совместимости и компоновку программы. Таким образом, будет решена задача автоматизации разработки математических моделей, предназначенных для решения конкретных задач проектирования, доводки и эксплуатации поршневых компрессоров.
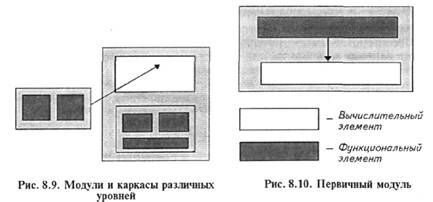
Основу СММ составляют первичные модули, т. е. такие модули, на вход которых подается только вектор коэффициентов X, задаваемых при расчете. В общем случае в первичном модуле может быть два элемента: функциональный и вычислительный (рис. 8.10). Причем вычислительный элемент может отсутствовать в том случае, если для определения величины Z достаточно функционального элемента, реализующего явную зависимость Z=f(X,Y), и нет необходимости в применении численных или других методов расчета. Первичный модуль может состоять из функциональной части (модуль-функция) или содержать в себе массив данных и алгоритм для определения какого-либо коэффициента (так называемый модуль-коэффициент).
Контрольные вопросы и задания. 1. Что такое модель? 2, Что такое моделирование? 3. Какие типы моделей вы знаете? 4. Что такое математическая модель? 5. Назовите главные особенности математических моделей. 6. Перечислите основные этапы процесса матемэтического моделирования. 7. Запишите на листе бумаги порядок работ, проводимых при математическом моделировании рабочих процессов поршневых компрессоров. 8. Каковы преимущества математического моделирования как исследовательского процесса? 9. Какими погрешностями определяется суммарная точность математического моделирования?