Многоканальная схема совместного обнаружения - оценивания

4. Методы приближенного расчета безусловного отношения правдоподобия. Схемы совместного обнаружения – оценивания.

Во многих случаях непосредственно выполнить интегрирование многомерной функции правдоподобия по распределению неизвестных параметров не удается. В этом случае используется один из двух возможных методов приближенного расчета безусловного отношения правдоподобия, приводящих к двум  существенно различным по виду, но по существу эквивалентным структурным схемам устройства обработки. Принципиальной  особенностью этих схем является возможность одновременно с решением о наличии сигнала получить оценку его априори неизвестных параметров, что оправдывает название “схемы совместного обнаружения – оценивания”.

4.1. Многоканальная схема совместного обнаружения – оценивания.

Возможность вычисления безусловного отношения правдоподобия с помощью многоканальной схемы базируется на замене интегралов конечными суммами и состоит в следующем.

Пусть область изменения неизвестного параметра представляет некоторый отрезок . Разобьем этот отрезок на  интервалов , границы которых обозначим . Тогда  (4.1),

 где  - априорное распределение неизвестного параметра.

Будем считать, что функция  непрерывна по . Тогда согласно обобщенной теореме о среднем для каждого интервала  существует принадлежащее этому интервалу значение параметра , обеспечивающее выполнение условия

,

где  - отношение правдоподобие, рассчитанное при значении параметра . Поэтому сумма (4.1) может быть представлена в виде

Рекомендуемые материалы

 (4.2),

где  - вероятность того, что параметр  принадлежит  интервалу. Из формулы  (4.2) следует, что безусловное отношение правдоподобия представляет собой выборочное среднее значений парциальных статистик.

Соответствующую формуле (4.2) схему обработки можно представить в виде некоторого  - канального устройства, каждый канал которого настроен на некоторое фиксированное значение неизвестного параметра . Очевидно, что при , т.е. при неограниченном увеличении числа  интервалов разбиения, сумма (4.2) независимо от способа разбиения сходится к значению интеграла (4.1), т.е. при  изображенная на рис.4.1 схема реализует обработку, близкую к оптимальной.

Поскольку, как отмечено выше, способ разбиения диапазона значений неизвестного параметра на интервалы  мало влияет на характеристики алгоритма этот способ может выбираться исходя из удобства расчетов; например исходя из условия, чтобы вероятность  попадания параметра для всех интервалов была одинаковой: .

Если неизвестный параметр  является измеряемым, т.е. его значение после обнаружения сигнала представляет самостоятельный интерес, то максимально правдоподобная оценка этого параметра   соответствует значению параметра  , при котором . Выбор номера соответствующего канала и выдачу на выход оценки неизвестного параметра  обеспечивают схема поиска максимума и ключ, открываемый в момент принятия решения об обнаружении сигнала.

Рассмотренная схема позволяет дать приближенную количественную оценку влияния  априорной неопределенности на  параметры обнаружителя, использующего статистику безусловного отношения правдоподобия. Для этого проанализируем ход накопления статистики  в каналах, содержащих и не содержащих сигнал.

Обозначим через  индекс канала, содержащего сигнал. Очевидно, что формула (4.2) может быть представлена в виде двух слагаемых

 (4.3)

В каналах, где сигнал от цели отсутствует, среднее значение статистики  на любом шаге равно единице:

Вместе с этой лекцией читают "24 Глазные растворы".

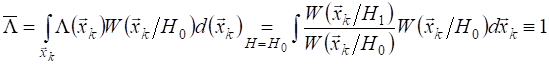
(тождество отражает условие нормировки плотности ). Следовательно, мат. ожидание второго слагаемого формулы (4.3) равно . В канале, содержащем цель, , поэтому отношение правдоподобия этого канала нарастает (в среднем) по геометрической прогрессии  (мат. ожидание произведения независимых величин равно произведению их мат. ожиданий). Следовательно мат. ожидание статистики (4.2) может быть записано в виде:

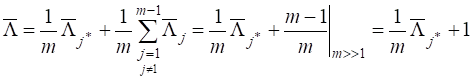
Рис.4.2.

Таким образом, “вклад” канала, содержащего сигнал, в безусловное отношение правдоподобия  по мере наблюдения нарастает, т.е. суммарный отклик схемы (4.2) стремится к отклику канала, “согласованного” с сигналом (схема как бы настраивается на истинное значение априори неизвестного параметра, см. рис.4.2). Наличие “пустых” каналов при этом учитывается коэффициентом , характеризующим “плату” за априорную неопределенность. За счет этого коэффициента среднее приращение логарифма отношения правдоподобия (информация Кульбака – Леблера) уменьшается примерно на .

Возможна и другая, эквивалентная, трактовка полученных результатов: уменьшение отношения правдоподобия в  раз равнозначно увеличению в  раз решающего порога, что соответствует увеличению длительности наблюдения примерно в  раз.