Исчисление высказываний
3. Лекция: Исчисление высказываний
Напомним, что тавтологией мы называли пропозициональную формулу, истинную при всех значениях переменных. Оказывается, что все тавтологии можно получить из некоторого набора "аксиом" с помощью "правил вывода", которые имеют чисто синтаксический характер и никак не апеллируют к смыслу формулы, ее истинности и т. д. Эту задачу решает так называемое исчисление высказываний. В этой лекции мы перечислим аксиомы и правила вывода этого исчисления, и приведем несколько доказательств теоремы о полноте (которая утверждает, что всякая тавтология выводима в исчислении высказываний).
Исчисление высказываний (ИВ)
Каковы бы ни были формулы  , следующие формулы называют аксиомами исчисления высказываний:
, следующие формулы называют аксиомами исчисления высказываний:
|
| (1) |
|
| (2) |
|
| (4) |
|
| (5) |
|
| (6) |
|
| (7) |
|
| (8) |
|
| (9) |
|
| (10) |
|
| (11) |
Как говорят, мы имеем здесь одиннадцать "схем аксиом"; из каждой схемы можно получить различные конкретные аксиомы, заменяя входящие в нее буквы на пропозициональные формулы.
Единственным правилом вывода исчисления высказываний является правило со средневековым названием "modus ponens" (MP). Это правило разрешает получить (вывести) из формул  и
и  формулу
формулу  .
.
Выводом в исчислении высказываний называется конечная последовательность формул, каждая из которых есть аксиома или получается из предыдущих по правилу modus ponens.
Вот пример вывода (в нем первая формула является частным случаем схемы (1), вторая — схемы (2), а последняя получается из двух предыдущих по правилу modus ponens):
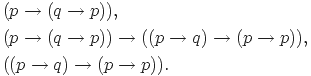
Пропозициональная формула  называется выводимой в исчислении высказываний, или теоремой исчисления высказываний, если существует вывод, в котором последняя формула равна
называется выводимой в исчислении высказываний, или теоремой исчисления высказываний, если существует вывод, в котором последняя формула равна  . Такой вывод называют выводом формулы
. Такой вывод называют выводом формулы  . (В принципе можно было бы и не требовать, чтобы формула
. (В принципе можно было бы и не требовать, чтобы формула  была последней — все дальнейшие формулы можно просто вычеркнуть.)
была последней — все дальнейшие формулы можно просто вычеркнуть.)
Как мы уже говорили, в исчислении высказываний выводятся все тавтологии и только они. Обычно это утверждение разбивают на две части: простую и сложную. Начнем с простой:
Теорема 17 (О корректности ИВ). Всякая теорема исчисления высказываний есть тавтология.
Несложно проверить, что все аксиомы — тавтологии. Для примера проделаем это для самой длинной аксиомы (точнее, схемы аксиом) — для второй. В каком случае формула  (где
(где  — некоторые формулы) могла бы быть ложной? Для этого посылка
— некоторые формулы) могла бы быть ложной? Для этого посылка  должна быть истинной, а заключение
должна быть истинной, а заключение  — ложным. Чтобы заключение было ложным, формула
— ложным. Чтобы заключение было ложным, формула  должна быть истинной, а формула
должна быть истинной, а формула  — ложной. Последнее означает, что
— ложной. Последнее означает, что  истинна, а
истинна, а  ложна. Таким образом, мы знаем, что
ложна. Таким образом, мы знаем, что  ,
,  и
и  истинны. Отсюда следует, что
истинны. Отсюда следует, что  и
и  истинны, и потому
истинны, и потому  истинна — противоречие. Значит, наша формула не бывает ложной.
истинна — противоречие. Значит, наша формула не бывает ложной.
Корректность правила MP также очевидна: если формулы  и
и  всегда истинны, то по определению импликации формула
всегда истинны, то по определению импликации формула  также всегда истинна. Таким образом, все формулы, входящие в выводы (все теоремы) являются тавтологиями.
также всегда истинна. Таким образом, все формулы, входящие в выводы (все теоремы) являются тавтологиями.
Гораздо сложнее доказать обратное утверждение.
Теорема 18 (О полноте ИВ). Всякая тавтология есть теорема исчисления высказываний.
Мы предложим несколько альтернативных доказательств этой теоремы. Но, прежде всего мы должны приобрести некоторый опыт построения выводов и использования аксиом.
Лемма 1. Какова бы ни была формула  , формула
, формула  является теоремой.
является теоремой.
Докажем лемму, предъявив вывод формулы  в исчислении высказываний.
в исчислении высказываний.
![Описание: ({Dto((Dto D)to D))}hmto{((Dto(D to D))to(Dto D))}]() [аксиома 2 при
[аксиома 2 при ![Описание: A=D]() ,
, ![Описание: B=(Dto D)]() ,
, ![Описание: C=D]() ];
]; ![Описание: Dto((Dto D)to D)]() [аксиома 1];
[аксиома 1]; ![Описание: (Dto(Dto D))to(Dto D)]() [из 1 и 2 по правилу MP];
[из 1 и 2 по правилу MP]; ![Описание: Dto(Dto D)]() [аксиома 1];
[аксиома 1]; ![Описание: (Dto D)]() [из 3 и 4 по правилу MP].
[из 3 и 4 по правилу MP].
Как видно, вывод даже такой простой тавтологии, как  , требует некоторой изобретательности. Мы облегчим себе жизнь, доказав некоторое общее утверждение о выводимости.
, требует некоторой изобретательности. Мы облегчим себе жизнь, доказав некоторое общее утверждение о выводимости.
Часто мы рассуждаем так: предполагаем, что выполнено какое-то утверждение  , и выводим различные следствия. После того как другое утверждение
, и выводим различные следствия. После того как другое утверждение  доказано, мы вспоминаем, что использовали предположение
доказано, мы вспоминаем, что использовали предположение  , и заключаем, что мы доказали утверждение
, и заключаем, что мы доказали утверждение  . Следующая лемма, называемая иногда "леммой о дедукции", показывает, что этот подход правомерен и для исчисления высказываний.
. Следующая лемма, называемая иногда "леммой о дедукции", показывает, что этот подход правомерен и для исчисления высказываний.
Пусть  — некоторое множество формул. Выводом из
— некоторое множество формул. Выводом из  называется конечная последовательность формул, каждая из которых является аксиомой, принадлежит
называется конечная последовательность формул, каждая из которых является аксиомой, принадлежит  или получается из предыдущих по правилу MP. (Другими словами, мы как бы добавляем формулы из
или получается из предыдущих по правилу MP. (Другими словами, мы как бы добавляем формулы из  к аксиомам исчисления высказываний — именно как формулы, а не как схемы аксиом.) Формула
к аксиомам исчисления высказываний — именно как формулы, а не как схемы аксиом.) Формула  выводима из
выводима из  , если существует вывод из
, если существует вывод из  , в котором она является последней формулой. В этом случае мы пишем
, в котором она является последней формулой. В этом случае мы пишем  . Если
. Если  пусто, то речь идет о выводимости в исчислении высказываний, и вместо
пусто, то речь идет о выводимости в исчислении высказываний, и вместо  пишут просто
пишут просто  .
.
Лемма 2 (о дедукции). Пусть  — множество формул. Тогда
— множество формул. Тогда  тогда и только тогда, когда
тогда и только тогда, когда  .
.
В одну сторону утверждение почти очевидно: пусть  . Тогда и
. Тогда и  . (Для краткости мы опускаем фигурные скобки и заменяем знак объединения запятой). По определению
. (Для краткости мы опускаем фигурные скобки и заменяем знак объединения запятой). По определению  , откуда по MP получаем
, откуда по MP получаем  .
.
Пусть теперь  . Нам надо построить вывод формулы
. Нам надо построить вывод формулы  из
из  . Возьмем вывод
. Возьмем вывод  формулы
формулы  из
из  . Припишем ко всем формулам этого вывода слева посылку
. Припишем ко всем формулам этого вывода слева посылку  :
: 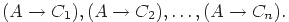
Эта последовательность оканчивается на  . Сама по себе она не будет выводом из
. Сама по себе она не будет выводом из  , но из нее можно получить такой вывод, добавив недостающие формулы, и тем самым доказать лемму о дедукции.
, но из нее можно получить такой вывод, добавив недостающие формулы, и тем самым доказать лемму о дедукции.
Будем добавлять эти формулы, двигаясь слева направо. Пусть мы подошли к формуле  . По предположению формула
. По предположению формула  либо совпадает с
либо совпадает с  , либо принадлежит
, либо принадлежит  , либо является аксиомой, либо получается из двух предыдущих по правилу MP. Рассмотрим все эти случаи по очереди.
, либо является аксиомой, либо получается из двух предыдущих по правилу MP. Рассмотрим все эти случаи по очереди.
(1) Если  есть
есть  , то очередная формула имеет вид
, то очередная формула имеет вид  . По лемме 1 она выводима, так что перед ней мы добавляем ее вывод.
. По лемме 1 она выводима, так что перед ней мы добавляем ее вывод.
(2) Пусть  принадлежит
принадлежит  . Тогда мы вставляем формулы
. Тогда мы вставляем формулы  и
и  (аксиома 1). Применение правила MP к этим формулам дает
(аксиома 1). Применение правила MP к этим формулам дает  , что и требовалось.
, что и требовалось.
(3) Те же формулы можно добавить, если  является аксиомой исчисления высказываний.
является аксиомой исчисления высказываний.
(4) Пусть, наконец, формула  получается из двух предыдущих формул по правилу MP. Это значит, что в исходном выводе ей предшествовали формулы
получается из двух предыдущих формул по правилу MP. Это значит, что в исходном выводе ей предшествовали формулы  и
и  . Тогда в новой последовательности (с добавленной посылкой
. Тогда в новой последовательности (с добавленной посылкой  ) уже были формулы
) уже были формулы  и
и  . Поэтому мы можем продолжить наш
. Поэтому мы можем продолжить наш  -вывод, написав формулы
-вывод, написав формулы  (аксиома 2);
(аксиома 2);  (modus ponens);
(modus ponens);  (modus ponens).
(modus ponens).
Люди также интересуются этой лекцией: 5. Английская журналистика в годы второй мировой войны.
Итак, во всех четырех случаях мы научились дополнять последовательность до вывода из  , так что лемма о дедукции доказана.
, так что лемма о дедукции доказана.
20. Докажите, что для любых формул  формула
формула  выводима в исчислении высказываний. (Указание: используйте лемму о дедукции и тот факт, что
выводима в исчислении высказываний. (Указание: используйте лемму о дедукции и тот факт, что  .)
.)
21. Докажите, что если  и
и  , то
, то  . (Это свойство иногда называют "правилом сечения" (cut);говорят, что формула
. (Это свойство иногда называют "правилом сечения" (cut);говорят, что формула  "отсекается" или "высекается". Сходные правила играют центральную роль в теории доказательств, где формулируется и доказывается "теорема об устранении сечения" для различных логических систем).
"отсекается" или "высекается". Сходные правила играют центральную роль в теории доказательств, где формулируется и доказывается "теорема об устранении сечения" для различных логических систем).
22. Добавим к исчислению высказываний, помимо правила modus ponens, еще одно правило, называемое правилом подстановки. Оно разрешает заменить в выведенной формуле все переменные на произвольные формулы (естественно, вхождения одной переменной должны заменяться на одну и ту же формулу). Покажите, что после добавления такого правила класс выводимых формул не изменится, но теорема о дедукции перестанет быть верной.
Заметим, что мы пока что использовали только две первые аксиомы исчисления высказываний. Видно, кстати, что они специально подобраны так, чтобы доказательство леммы о дедукции прошло.
Другие аксиомы описывают свойства логических связок. Аксиомы  и
и  говорят, какие следствия можно вывести из конъюнкции (
говорят, какие следствия можно вывести из конъюнкции ( и
и  ). Напротив, аксиома 5 говорит, как можно вывести конъюнкцию. Из нее легко следует такое правило: если
). Напротив, аксиома 5 говорит, как можно вывести конъюнкцию. Из нее легко следует такое правило: если  и
и  , то
, то  (применяем эту аксиому и дважды правило MP). Часто подобные правила записывают так:
(применяем эту аксиому и дважды правило MP). Часто подобные правила записывают так:  (над чертой пишут "посылки" правила, а снизу — его "заключение", вытекающее из посылок).
(над чертой пишут "посылки" правила, а снизу — его "заключение", вытекающее из посылок).

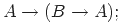
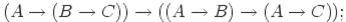
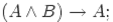
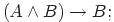
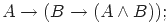
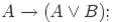
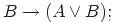
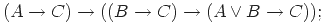
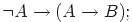
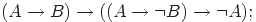
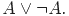
 [аксиома 2 при
[аксиома 2 при  ,
,  ,
,  ];
];  [аксиома 1];
[аксиома 1];  [из 1 и 2 по правилу MP];
[из 1 и 2 по правилу MP];  [аксиома 1];
[аксиома 1]; 















