Кривые 2-го порядка. Сплайны. Кривые Безье

Лекция 9

Кривые 2-го порядка. Сплайны. Кривые Безье

Кривые второго порядка

Общий вид уравнения линии 2-го порядка:

a₁x²+a₂y²+a₃xy+a₄x+a₅y+a₆=0.

Рассмотрим различные формы линий 2-го порядка.

Уравнение окружности:

(x-x₀)²+(y-y₀)²=r² – нормальное уравнение окружности,

C(x₀, y₀) – центр окружности,

Рекомендуемые материалы

M(x,y) – произвольная точка окружности,

x²+y²+ax+by+g=0,

a=-2x₀;  b=-2y₀;  g=x₀²+y₀²-r².

Ax²+Ay²+Dx+Ey+F=0 – общее уравнение окружности.

Действительная окружность при   (a²+b²)/4-g³0,  где a=D/A; b=E/A; g=F/A.

Таким образом, действительная кривая 2-го порядка является окружностью тогда и только тогда, когда:

1) коэффициенты при квадратах текущих координат равны между собой;

2) отсутствует член, содержащий произведение текущих координат.

Центральные кривые 2-го порядка – кривые, имеющие собственный центр симметрии.

A(x-x₀)²+C(y-y₀)²=D,     A¹C.

O(x₀, y₀) – центр симметрии кривой;

x=x₀,  y=y₀ – оси симметрии кривой.

Пусть x₀=0 и  y₀=0.

Кривая 2-го порядка принадлежит эллиптическому типу, если коэффициенты A и C имеют одинаковые знаки, т.е. AC>0.

Пусть A>0 и C>0, тогда если:

● D>0 – действительный эллипс, x²/a²+y²/b²=1 – каноническое уравнение эллипса;

● D=0 – вырожденный эллипс (кривая вырождается в точку);

● D<0 – мнимый эллипс.

Кривая 2-го порядка является кривой гиперболического типа, если коэффициенты A и C имеют противоположные знаки, т.е. AC<0.

Пусть A>0, тогда C<0:

● если D>0 – гипербола (рис. 7), x²/a²-y²/b²=1 – каноническое уравнение гиперболы;

● если D=0 – вырожденная гипербола представляет собой пару пересекающихся прямых

;

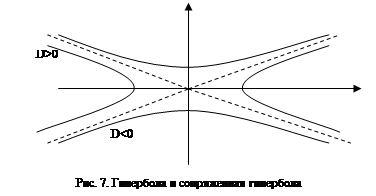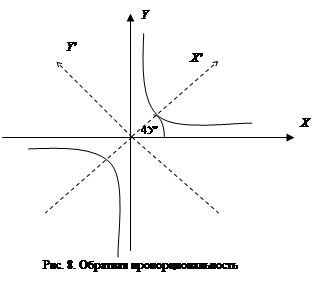
● если D<0 – сопряженная гипербола (рис. 7),  xy=a² (a>0) – обратная пропорциональность. Графиком является равнобочная гипербола (к уравнению гиперболы легко прийти, повернув оси координат на 45 º – рис. 8).

Нецентральные кривые 2-го порядка не имеют центра симметрии или имеют бесконечное множество центров, могут иметь ось симметрии.

(y-y₀)²=2p(x-x₀) – парабола,  O(x₀, y₀) – вершина параболы,
P – параметр параболы.

Если вершина параболы находится в начале координат и p>0, то y²=2px – каноническое уравнение параболы.

Параметрические уравнения линий.

Параметрическое уравнение окружности:

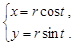
Параметрическое уравнение эллипса:

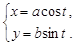
Параметрическое уравнение параболы:

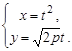
Циклоида (кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии):

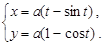
Спираль Архимеда:   r=aj  (a>0) – уравнение в полярных координатах.

Сплайны. Кривые Безье

Сплайн – гладкая кривая, которая проходит через две или более опорных точек, а также имеет расположенные вне ее управляющие точки, влияющие на форму сплайна. Наиболее общие типы сплайнов – кривые Безье и B-сплайны (B-spline curves). Типичным примером сплайнов являются также неоднородные рациональные B-сплайны (Non-Uniform Rational B-Spline – NURBS). Сплайны состоят из вершин (Vertices) и сегментов (Segments). Каждая вершина сплайна имеет касательные векторы (Tangents), снабженные на концах управляющими точками, или маркерами (Handels). Маркеры касательных векторов управляют кривизной сегментов сплайна при входе в вершину, которой принадлежат касательные векторы, и выходе из нее.

Кривые Безье  разработаны математиком Пьером Безье. Кривые и поверхности Безье использовались в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов автомобилей. В настоящее время они широко используются в компьютерной графике.

Кривые Безье описываются в параметрической форме:

x=P_x(t),      y=P_y(t).

Значение t выступает как параметр, которому отвечают координаты отдельной точки линии.

Многочлены Безье для P_x и P_y имеют следующий вид:

  

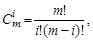
где  C_mⁱ  – сочетание m по i, а x_i, y_i  – координаты точек ориентиров P_i. Значение m можно рассматривать и как степень полинома, и как значение, которое на единицу меньше количества точек-ориентиров.

Рассмотрим кривые Безье, классифицируя их по значени-
ям  m.

m=1 (по двум точкам). Кривая вырождается в отрезок прямой линии, определяемой концевыми точками P₀  и P₁. Параметрическое уравнение:

P(t)=(1-t)P₀ + tP₁.

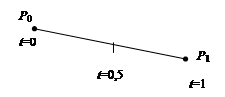m=2 (по трем точкам). Параметрическое уравнение:

P(t)=(1-t)²P₀ + 2t(1-t)P₁ + t²P₂.

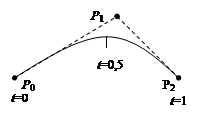m=3 (по четырем точкам – кубическая). Используется довольно часто, в особенности в сплайновых кривых. Параметрическое уравнение:

P(t)=(1-t)³P₀ + 3t(1-t)²P₁ + 3t²(1-t)P₂ + t³P₃.

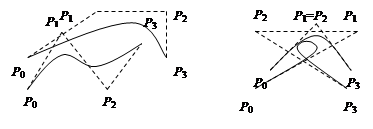Геометрический алгоритм для кривой Безье  позволяет вычислить координаты (x, y) точки кривой Безье по значению параметра t (рис. 9).

1. Каждая сторона контура многоугольника, проходящего по точкам-ориентирам, делится пропорционально значению t.

2. Точки деления соединяются отрезками прямых и образуют новый многоугольник. Количество узлов нового контура на единицу меньше, чем количество узлов предыдущего контура.

3. Стороны нового контура снова делятся пропорционально значению t и т.д. Это продолжается до тех пор, пока не будет получена единственная точка деления – точка кривой Безье.

Сегмент кривой Безье 3-го порядка описывается положением четырех точек. Две из них являются опорными (узлами кривой): начальная точка P₀ (x₀, y₀) и конечная P₃ (x₃, y₃). Точки P₁ (x₁, y₁)  и P₂ (x₂, y₂), определяющие положение касательных относительно отрезка, называются управляющими. Метод построения кривой Безье основан на использовании пары касательных (управляющих линий), проведенных к сегменту кривой в его окончаниях. На форму кривой влияют угол наклона касательной и длина ее отрезка.

Параметрическое уравнение Безье описывает положение точек и, тем самым, форму кривой. Уравнение решают относительно параметра t, принимающего значения от 0 (в начальной точке) до 1 (в конечной точке). При построении сегмента кривой Безье на плоскости рассчитывают координаты x и y (для четырех точек, из них двух управляющих):

R(t)=P₀(1-t)³ + P₁t(1-t)² + P₂t²(1-t) + P₃t³,   где 0<t<1;

x(t)=a_xt³ + b_xt² + c_xt + x₀;

x₁=x₀ + (c_x:3);   x₂=x₁ + [(c_x+b_x):3];   x₃=x₀ + c_x + b_x + a_x;

y(t)= a_yt³ + b_yt² + c_yt + y₀;

y₁=y₀ + (c_y:3);   y₂=y₁ + [(c_y+b_y):3];   y₃=y₀ + c_y + b_y + a_y.

Следовательно:

c_x=3(x₁-x₀);   b_x=3(x₂-x₁)-c_x;   a_x=x₃ - x₀ - c_x - b_x; 

c_y=3(y₁-y₀);   b_y=3(y₂-y₁)-c_y;   a_y=y₃ - y₀ - c_y - b_y.

Значение t определяет степень влияния точек на форму кривой. Например, при t=0,333 наибольший "вес" приобретает точка P₁, а при t=0,666 – точка P₂.  Из приведенных уравнений вытекает, что кривая может проходить лишь через начальную и конечную опорные точки сегмента (P₀, P₃). Тем самым достигаются простота описания и стабильность кривой Безье.

Кривые Безье обладают рядом свойств, определяющих возможность их использования в векторной графике. С геометрической точки зрения, производной кривой Безье будет другая кривая Безье, векторы управляющих точек которой определяются вычислением разностей векторов управляющих точек исходной кривой.

Основные свойства кривой Безье:

● непрерывность заполнения сегмента между начальной и конечной точками;

● кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;

● при наличии только двух контрольных точек сегмент представляет собой отрезок прямой линии;

● прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;

● кривая Безье симметрична, т.е. обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;

Лекция 6 - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

● масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она, с математической точки зрения, "аффинно инвариантна";

● изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;

● степень кривой всегда на единицу меньше числа опорных точек (т.е. при трех опорных точках форма кривой - парабола);

● размещение дополнительных опорных точек вблизи одной позиции увеличивает ее "вес" и приводит к приближению траектории кривой к данной позиции;

● окружность не может быть описана параметрическим уравнением кривой Безье;

● невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).