Многоугольники (полигоны)

Лекция 10

Многоугольники (полигоны). Тесты ориентации точки относительно полигона

Понятие полигона. Геометрическая модель плоского
полигона

Контур полигона определяется вершинами, которые соединены отрезками прямых. В векторной форме полигон задается перечислением своих вершин: P={p₁, p₂, …, p_n, p₁}.

С учетом принятого соглашения о правой ориентации нормали относительно направляющего вектора внешняя ориентация нормалей к сторонам полигона обеспечивается при его обходе против часовой стрелки.

Свойства плоских многоугольников

Пересечение прямой линии с полигоном. Прямая пересекает полигон, если существует хотя бы одна пара вершин, лежащих от нее по разные стороны (это свойство предполагает сравнение для всех имеющихся пар вершин, а не только смежных).

Выпуклость полигона. У выпуклого полигона все углы
Ð p_i-1 p_i p_i+1 одного знака. Другими словами, при обходе выпуклого полигона по замкнутому контуру в произвольном направлении каждая вершина p_i+1 расположена относительно ребра p_i-1 p_i одинаково для всех значений i: слева при положительном направлении обхода и справа при отрицательном.

Самопересечение полигона. Полигон является самопересекающейся замкнутой ломаной линией, если у него существует хотя бы одна пара пересекающихся отрезков. Два отрезка пересекаются друг с другом, если концы одного находятся по разные стороны от прямой другого и наоборот (тестироваться должны все пары несмежных ребер полигона).

Рекомендуемые материалы

Тесты ориентации точки относительно полигона

1. Выпуклый тест. Определяет положение точки относительно полигона (рис. 10): внешняя точка, внутренняя точка, граничная точка (внешнее подпространство полигона считается положительным, внутреннее – отрицательным, граница соответствует нулю).

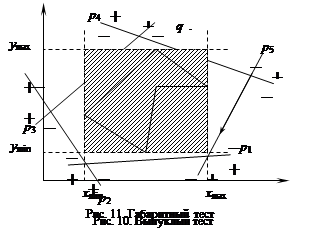2. Габаритный тест. Определяет гарантированную непринадлежность точки q произвольному полигону P путем сравнения ее координат с габаритами полигона – минимальными и максимальными координатами его вершин. Полностью задачу ориентации габаритный тест не решает, тем не менее, благодаря своей простоте, применяется во многих алгоритмах для быстрого обнаружения заведомо непересекающихся геометрических объектов (рис. 11).

3. Угловой тест. Основан на вычислении и анализе алгебраической суммы углов d_i=Ð(V_i, V_i+1) между смежными векторами V_i=p_i-q, соединяющими точку q с вершинами p_i, при обходе произвольного полигона P по замкнутому контуру в произвольном направлении.

Точка является внутренней, если сумма углов ∑d_i=2 π  (рис. 12). Точка  является  внешней, если  сумма  углов  ∑d_i=0  (рис. 13).

Точка является граничной (принадлежит границе полигона):

● если при расчете векторов получен нулевой вектор çV_iç=0, то тестируемая точка совпадает с вершиной p_i;

● если при расчете углов d_i получен развернутый угол с модулем | d_i | = π, то тестируемая точка лежит на ребре p_i p_i+1.

Злокачественные опухоли яичников - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Существуют две разновидности  углового теста – радианный и октантный.

Лучевой тест ориентации точки q относительно полигона p заключается в выпускании из этой точки в произвольном направлении V луча  p(t)=q+Vt    (" t > 0) и подсчете числа его пересечений с ребрами p.  Анализ пар дает следующие критерии ориентации точки относительно полигона: точка является внутренней, если число пар нечетно (t_i>0, 0<t_i<1); точка является внешней, если число пар четно, в том числе равно нулю; точка лежит на границе p, если найдется хотя бы одна пара, для которой t_i=0, 0£t_i£1.

Особенности лучевого теста (рис. 14):

● неопределенность числа пересечений при прохождении луча точно через вершину p_i при t_i=1 или вершину p_i+1 при t_i=0. Необходимо повторить тест заново с другим направлением луча V;

● требуется расчет параметров пересечения луча со всеми ребрами полигона.

Исследуются параметры пересечения луча с отрезками p_i+(p_i+1–p_i)t,  "0£t£1.