Геометрические модели плоских объектов
Лекция 8
Геометрические модели плоских объектов
Основные понятия
Положение точки в пространстве Rn (n-мерном пространстве) задается радиус-вектором p=[p1, p2, …, pn], имеющим n координат p1, p2, …, pn и разложение по n линейно-независимым базисным векторам e1, e2, …, en :
 .
.
Таким образом положение точки на плоскости определяется радиус-вектором точки p=[px, py]= pxex +pyey или p=[r, φ] в полярной системе координат.
Расстояние между двумя точками p1 и p2 равно:
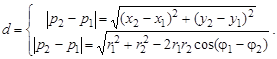
Линия на плоскости может быть задана с помощью уравнения в неявной форме:
Рекомендуемые материалы
(НФ) f(x,y)=0;
или в параметрической форме:
(ПФ) p(t)=[x(t), y(t)].
В любой регулярной (гладкой и некратной) точке на линии p0=[x0, y0]=p(t0) возможна линеаризация кривой, т.е. проведение к ней касательной прямой, уравнения которой имеют вид
(НФ) Nx(x - x0) + Ny(y - y0) = 0 или N ◦ (p - p0) = 0,
(ПФ) x(t) = x0 + Vx t, y(t)= y0 + Vy t или p(t) = p0 + Vt.
Вектор нормали N=[Nx, Ny] ортогонален линии и направлен в ту сторону, где f(p)> 0.
Направляющий вектор линии V=[Vx, Vy] начинается в точке p0 и направлен по касательной к p(t) в сторону увеличения t.
Векторы N и V ортогональны, т.е. N ◦ V = 0 или NxVx + NyVy = 0.
Связь вектора нормали и направляющего вектора:
N=[Vy, - Vx], V=[-Ny, Nx]
Способы описания (модели) прямой линии
Неявное уравнение прямой задается тремя коэффициентами A, B и D, составляющими вектор F=[A, B, D]:
(НФ): Ax+By+D=0.
Хотя бы одно из чисел A или B должно быть ненулевым.
Если оба коэффициента ненулевые (A≠0 и B≠0), то прямая проходит наклонно к осям координат и пересекается с ними в точках (-D/A, 0) и (0, -D/B).
При A=0, B≠0 уравнение By+D=0 описывает горизонтальную прямую y= –D/B .
При A≠0, B=0 уравнение Ax+D=0 описывает вертикальную прямую x= –D/A.
Прямая проходит через начало координат: f(0,0)=0 при D=0.
Благодаря свойству прямой разделять плоскость на две полуплоскости с противоположными знаками, неявное уравнение позволяет определять положение точки (точек) на плоскости относительно прямой:
1) точка q лежит на прямой, если f(q)=0;
2) точки a и b лежат по одну сторону от прямой, если f(a)∙f(b)>0;
3) точки a и b лежат по разные стороны от прямой, если f(a)∙f(b)<0.
Для построения прямой по неявному уравнению необходимо и достаточно иметь либо две несовпадающие точки p0 и p1, через которые она проходит, либо точку p0 и направляющий вектор V, с помощью которого вторая точка p1 вычисляется как p1=p0+V.
Из неявного уравнения прямой N=[A, B] Þ V=[-B, A].
Нормальное уравнение прямой – прямая описывается с помощью точки p0 и вектора нормали N и выводится из условия ортогональности векторов N и (p-p0) для всех точек p, принадлежащих прямой f(p)=N◦(p-p0).
Неявная функция позволяет оценить положение точки p относительно вектора нормали прямой:
● при f(a)>0 точка a лежит в том же полупространстве, куда направлена нормаль, а угол Ð(a-p0, N) острый;
● при f(b)<0 угол Ð(b-p0, N) тупой, а точка b и нормаль находятся по разные стороны от прямой.
Параметрическая функция прямой p(t)=p0+Vt, где
V=[-Ny, Nx] удобна для задания и построения частей прямой – отрезков и лучей. Для этого необходимо указать пределы изменения параметра t:
● бесконечный интервал -¥<t<¥ не ограничивает протяженность бесконечной прямой;
● при t³0 получается луч, выходящий из точки p0 в бесконечность в направлении вектора V;
● конечный интервал t0≤t≤t1 определяет отрезок прямой между точками p0+Vt0 и p0+Vt1.
Благодаря левой ориентации направляющего вектора V относительно вектора нормали N эквивалентная нормальной форме функция
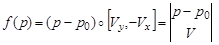
позволяет определить положение точки относительно направления движения по прямой:
● при f(a)>0 точка a лежит справа от точки p0, так что угол Ð(a-p0, V) положительный;
● при f(b)<0 угол Ð(b-p0, V) отрицательный, а точка b лежит слева от точки p0.
Неявная форма уравнения прямой, проходящей через две точки a=[ax, ay] и b=[bx,by], выводится из условия принадлежности прямой этих точек и точки p=[x,y].
Выбрав направление движения по прямой от точки a к точке b, получим направляющий вектор V=b-a и параметрическую модель линии:
(ПФ): x(t)=ax+(bx-ax)t, y(t)= ay+(by-ay)t или p(t)=a+(b-a)t.
Условие существования прямой очевидное: V≠0, т.е. a≠b.
При изменении параметра t от 0 до 1 движение точки происходит внутри отрезка ab от точки a до точки b.
Взаимное расположение графических элементов на плоскости
1. Три точки p1, p2, p3 коллинеарны, т.е. лежат на одной прямой, если
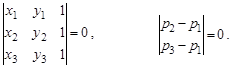 |
2. Точка p лежит на отрезке ab при нулевом угле между векторами p-a и b-p:
(p - a) ◦ (b - p)= |p - a|·|b - p| ,
 .
.
Взаимное расположение прямых.
1. Две прямые совпадают, если F1 × F2 =03 (векторное произведение равно нулевому вектору).
2. Две прямые параллельны, если

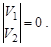
3. Две прямые ортогональны, если N1◦ N2=0 или V1◦ V2=0.
Взаимное расположение точки и прямой
1. Уравнение перпендикуляра, опущенного из точки
q=[qx, qy] на прямую, выглядит следующим образом:
(НФ): Ny(x-qx)-Nx(y-qy)=0,
(ПФ): p┴(t)=q+Nt или p┴(t)=q+V┴t , где V┴=[Vy, -Vx]=N.
2. Расстояние от точки q до прямой равно:

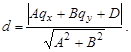
3. Зеркальное отражение точки q относительно прямой лежит на перпендикуляре к прямой на расстоянии 2d от q в сторону, противоположную проекции вектора q-p0 на нормаль N:
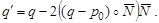
Пересечение двух прямых.
Пусть имеются две прямые, заданные уравнениями в НФ:
A1x+B1y+D1=0 и A2x+B2y+D2=0,
тогда координаты точки пересечения вычисляются следующим образом:

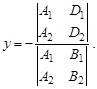
Возможны следующие три случая:
1. A1B2-A2B1≠0, т.е. A1/A2≠B1/B2 – прямые не параллельны, точка пересечения единственная и ее координаты вычисляются по вышеприведенным формулам.
2. A1B2-A2B1=0, D1B2-D2B1≠0 или A1D2-A2D1≠0 – прямые параллельны и точек пересечения нет.
3. A1B2-A2B1=0, D1B2-D2B1=0 и A1D2-A2D1=0, т.е. прямые совпадают во всех точках.
Угол между двумя пересекающимися прямыми находится как угол между векторами нормали или направляющими векторами Ð(N1, N2) = Ð(V1, V2).
Уравнения пучка прямых и биссектрисы угла
Уравнение пучка прямых, заключенных между двумя, прямыми определяется следующим образом:
(НФ)
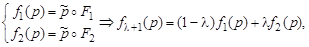
Информация в лекции "6.2. Организационно-технические мероприятия по световой маскировке" поможет Вам.
(ПФ)
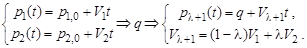
Изменение параметра пучка в интервале 0≤λ≤1 дает такие промежуточные прямые, что вращение происходит по кратчайшим углам.
Уравнение биссектрисы угла между двумя прямыми получается при λ=0,5, если |N1|=|N2| или |V1|=|V2|. В результате параметры биссектрисы можно найти по формулам
Fбис=|N2|F1+|N1|F2, pбис(t)=q+Vбисt, Vбис=|V2|V1+|V1|V2.
Расчет биссектрис бывает необходим, например, при построении окружности, вписанной в треугольник. Как известно, ее центр лежит в точке пересечения биссектрис внутренних углов этого треугольника. При построении биссектрисы внутреннего угла следует учитывать направления подставляемых в формулу векторов сторон треугольника: они должны либо оба выходить из вершины, либо оба входить в нее. При несоблюдении этого правила по указанной формуле будет проведена биссектриса дополнительного угла треугольника, а окружность окажется вневписанной.





















