Линейные модели оптимизации
Тема 10. Линейные модели оптимизации в управлении экономикой
Общая постановка задачи линейного программирования (ЗЛП)
Линейное программирование – это область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (max или min) линейной функции многих переменных при наличии линейных ограничений, то есть линейных равенств или неравенств, связывающих эти переменные.
С помощью задач линейного программирования решается широкий круг вопросов планирования экономических процессов, где ставится цель поиска наилучшего (оптимального) решения.
Найти вектор 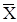 =(Х1, Х2, ..., Хn) максимизирующий линейную форму
=(Х1, Х2, ..., Хn) максимизирующий линейную форму
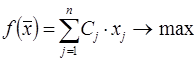 j=1, ..., n (7.1)
j=1, ..., n (7.1)
и удовлетворяющий условиям:
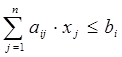 (7.2)
(7.2)
Рекомендуемые материалы
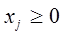 (7.3)
(7.3)
Линейная функция 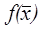 называется целевой функцией задачи, условия (7.2) - функциональными, а условия (7.3) – прямыми ограничениями задачи.
называется целевой функцией задачи, условия (7.2) - функциональными, а условия (7.3) – прямыми ограничениями задачи.
Вектор 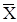 =(Х1, Х2, ..., Хn), компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП.
=(Х1, Х2, ..., Хn), компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП.
Все допустимые решения образуют область определения ЗЛП, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию 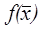 называется оптимальным планом задачи:
называется оптимальным планом задачи:
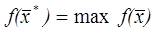
где 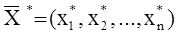 – оптимальное решение ЗЛП.
– оптимальное решение ЗЛП.
Будем считать, что ЗЛП записано в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с правой неотрицательной частью и все переменные неотрицательны.
Задачи оптимизации производственной
программы предприятия
В качестве критериев оптимальности будем использовать: прибыль, себестоимость, затраты станочного времени, номенклатуру произведенной продукции.
Неизвестным в задаче являются объемы выпуска продукции каждого вида. Введем следующие обозначения:
Хj, s – объем производства j-го продукта по s-му технологическому способу (j = 1,…, n); (s = 1,…, Qj);
n – количество видов выпускаемой продукции;
Qj – число технологических способов, используемых при производстве j-го продукта;
bi – наличие i-го ресурса (i = 1,…, m);
m – количество типов используемых ресурсов;
a i, j, s – норма затрат i-го ресурса на производство единицы j-го продукта по
s-му технологическому способу;
p j, s – прибыль от производства j-го продукта по s-му технологическому способу;
Tj – задание (госзаказ) по выпуску j-ого вида продукции;
C i, j – себестоимость производства j-го продукта по s-му технологическому способу;
Pi,j -- заданный уровень прибыли.
Задача на максимум прибыли
Используя принятые выше обозначения, модель задачи можно записать в следующем виде.
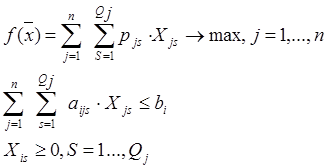
Выражение 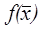 максимизирует совокупную прибыль всего объема выпускаемой продукции всех видов. В данной модели оптимизация возможна за счет включения в план выпуска наиболее выгодных видов продукции и за счет выбора для каждого вида продукции наиболее выгодных способов ее производства. Способы производства отличаются, друг от друга величиной удельной прибыли и нормами затрат ресурсов. Ограничения означают, что для любого из ресурсов его суммарный расход на производство всех видов продукции по всем способам не превосходит имеющихся ресурсов.
максимизирует совокупную прибыль всего объема выпускаемой продукции всех видов. В данной модели оптимизация возможна за счет включения в план выпуска наиболее выгодных видов продукции и за счет выбора для каждого вида продукции наиболее выгодных способов ее производства. Способы производства отличаются, друг от друга величиной удельной прибыли и нормами затрат ресурсов. Ограничения означают, что для любого из ресурсов его суммарный расход на производство всех видов продукции по всем способам не превосходит имеющихся ресурсов.
При составлении плана производства приходится учитывать не только ограниченность ресурсов, но и директивные задания (госзаказы) по выпуску продукции. При этом модель дополняется ограничением вида Xj>Tj, а свобода выбора значительно снижается.
Задача на минимум себестоимости производства
Экономико-математическая модель задачи имеет вид:
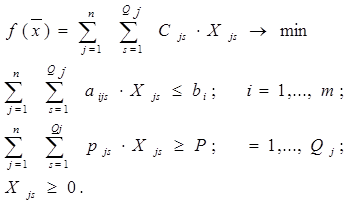
При построении модели на минимум затрат наличие ограничений типа «больше» или «равно» обязательно. Отсутствие ограничений снизу ведет к оптимальному плану с нулевыми значениями переменных, которые дадут наименьшее значение критерия оптимальности. Такое решение абсурдно с экономической точки зрения.
Все допустимые решения задачи, которой соответствует данная модель, различаются по видам затрат, но одинаковы с точки зрения результата. Результатом выступает заданная производственная программа. Выбор наилучшего плана производства по минимуму затрат возможен вследствие эквивалентности результатов по всем вариантам.
Следует подчеркнуть, что при различной величине результатов вариант с меньшими затратами может быть и не лучшим: просто с наименьшими затратами мы достигаем и меньшего результата.
Задача на максимум выпуска продукции в заданном
ассортиментном соотношении (на максимум комплексов)
Введем новые обозначения:
Kj – количество изделий вида j, которые входят в некоторый комплект (например, комплект запасных частей для автомобиля).
Функция максимума комплектной продукции будет следующая:
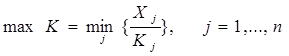 ,
,
то есть общее количество комплектов К определяется количеством изделий, из которых можно сформировать меньше всего «порций», объемом Kj . Эти изделия определяют, как бы «узкое место» в формировании комплектов, к максимальной «расшивке» которого следует стремиться.
Введем новое обозначение 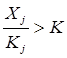 , которое связывает количество комплектов К с условием по формированию комплектов. Модель в общем виде с учетом наличия нескольких способов производства имеет следующий вид:
, которое связывает количество комплектов К с условием по формированию комплектов. Модель в общем виде с учетом наличия нескольких способов производства имеет следующий вид:
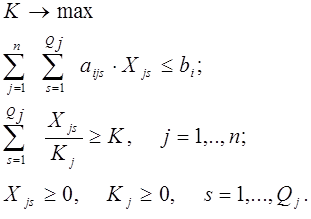
Задача на минимум затрат станочного времени
при заданной производственной программе
Для решения данной задачи преобразуем основные ограничения по фонду времени работы оборудования i-ой группы в управления путем ввода дополнительных неизвестных Zi, которые показывают резервный фонд времени i-ой группы оборудования в плане загрузки станков.
В результате система ограничений примет следующий вид:
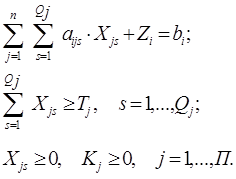
Общий расход полезного времени и его недоиспользовании при заданном фонде времени работы оборудования каждой группы связаны взаимно однозначным соответствием: минимуму затрат станочного времени соответствует максимум свободного резерва и наоборот. В связи с этим целевая функция, обеспечивающая минимуму станочного времени на выполнение заданной производственной программы, будет:
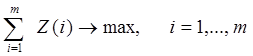
Одним из направлений в математическом моделировании экономических задач является использование свойств двойственной задачи, которая может быть сформулирована для любой задачи на оптимум. Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но также сделать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной задаче линейного программирования (ЗЛП).
Постановка двойственной задачи
Прямая задача Двойственная задача
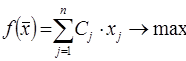 (7.1)
(7.1) 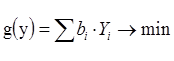 (7.4)
(7.4)
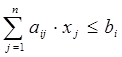 (7.2)
(7.2) 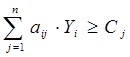 (7.5)
(7.5)
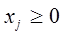 (7.3)
(7.3) 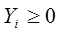 (7.6)
(7.6)
Согласно теории линейного программирования каждой ЗЛП вида (7.1) - (7.3) соответствует двойственная ей ЗЛП (7.4) - (7.6). Основные утверждения о взаимно двойственных задачах содержится в двух следующих теоремах:
Первая теорема двойственности
Для взаимодвойственных задач вида (7.1-7.3) и (7.4-7.6) возможен один из взаимоисключающих случаев:
1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают, то есть f(x)=g(Y).
2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пусто допустимое множество.
3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.
4. Обе рассматриваемые задачи имеют пустые допустимые множества.
Вторая теорема двойственности.
(теорема о дополняющей не жесткости)
Пусть вектор 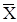 =(х1, х2, ..., хn) допустимое решение прямой задачи (7.1-7.3), а Y=(y1, y2, ..., ym) – допустимое решение двойственной задачи (7.4-7.6). Для того, чтобы они были оптимальными решениями, необходимо и достаточно, чтобы выполнялись следующие соотношения:
=(х1, х2, ..., хn) допустимое решение прямой задачи (7.1-7.3), а Y=(y1, y2, ..., ym) – допустимое решение двойственной задачи (7.4-7.6). Для того, чтобы они были оптимальными решениями, необходимо и достаточно, чтобы выполнялись следующие соотношения:
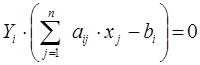 (7.7)
(7.7)
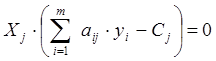 (7.8)
(7.8)
Условия (7.7) и (7.8) позволяют, если известно решение одной из взаимно двойственных задач найти оптимальное решение для другой задачи.
Теорема об оценках
Значения переменных Yi в оптимальном решении двойственной задачи представляет собой оценки влияния свободных членов bi системы ограничений - неравенств прямой задачи на величину ∆f(x):
∆ f (x) = ∆ bi .Yi (7.9)
Решая ЗЛП (7.1-7.3), симплексным методом, мы одновременно решаем и двойственную задачу ЗЛП (7.4-7.6). Переменные двойственной задачи Yi называется объектно-обусловленными оценками.
Экономическая интерпретация двойственной задачи
Рассмотрим экономическую интерпретацию двойственной задачи на следующих примерах.
Пример №1. Задача оптимального использования ресурсов
Для составления плана выпуска четырех видов продукции Р1-Р4 на предприятии используют три вида сырья S1-S3. Объемы выделенного сырья, нормы расхода сырья и прибыль, полученная в результате выпуска каждого вида продукции, приведем в следующей таблице 7.1.
Составим экономико-математическую модель задачи оптимального использования на максимум прибыли. В качестве неизвестных примем Xj - объем выпуска продукции j-го вида, где j=1,...,4.
Таблица 7.1.
| Вид сырья | Запасы сырья | Вид продукции. | |||
| Р1 | Р2 | Р3 | Р4 | ||
| S1 | 35 | 4 | 2 | 2 | 3 |
| S2 | 30 | 1 | 1 | 2 | 3 |
| S3 | 40 | 3 | 1 | 2 | 1 |
| ПРИБЫЛЬ | 14 | 10 | 14 | 11 |
Модель задачи:
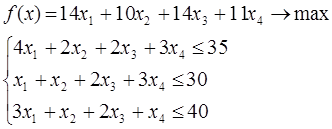 функциональные условия
функциональные условия
xj ≥ 0, j=1,…,4 - прямые ограничения.
Теперь сформулируем двойственную задачу. Пусть некая организация решила закупить все ресурсы рассматриваемого предприятия. При этом необходимо установить оптимальную цену на приобретаемые ресурсы у1, у2, у3, исходя из двух условий:
1. покупающая организация старается минимизировать общую стоимость ресурсов;
2. за каждый вид ресурсов надо уплатить не менее той суммы, которую хозяйство может выручить при переработке сырья в готовую продукцию.
Согласно первому условию общая стоимость сырья выражается величиной:
g(Y) = 35Y1 + 30Y2 + 40Y3 → min
Согласно второму требованию вводятся ограничения: на единицу первого вида продукции Р1 расходуются четыре единицы первого ресурса S1 ценой Y1, одна единица второго ресурса ценой Y2 и три единицы третьего ресурса ценой Y3. Стоимость всех ресурсов, расходуемых на производство единицы первого вида продукции, равна 4Y1 + Y2 + 3Y3 и должна составлять не менее 14, то есть 4Y1 + Y2 + 3Y3 ≥ 14.
В результате аналогичных рассуждений относительно производства остальных (2,3) видов продукции система неравенств примет следующий вид:
4Y1 + Y2 + 3Y3 ≥ 14
2Y1 + Y2 + Y3 ≥ 10
2Y1 + 2Y2 + 2Y3 ≥ 14
3Y1 + 3Y2 + Y3 ≥ 11
Цены ресурсов, естественно, должны быть неотрицательные: Y1≥0;Y2≥0;Y3≥0.
Получили симметричную пару взаимно двойственных задач. Для производственной программы 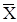 (х1,х2,…,хn) и при любом векторе оценок
(х1,х2,…,хn) и при любом векторе оценок 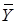 =(Y1,Y2,…,Ym) выполняется неравенство
=(Y1,Y2,…,Ym) выполняется неравенство
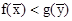 , то есть ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит, величина
, то есть ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит, величина 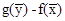 характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов.
характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов.
Из первой теоремы двойственности следует, что при оптимальных производственной программе и векторе оценок ресурсов, производственные потери равны нулю.
Согласно второй теоремы, предъявляются следующие требования:
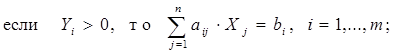
 (7.10)
(7.10)
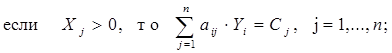
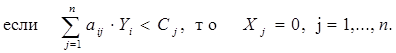 (7.11)
(7.11)
Условия (7.10) можно интерпретировать так: если оценка Yi единицы ресурса i-го вида положительна, то при оптимальной производственной программе этот ресурс используется полностью. Если же ресурс используется не полностью, то его оценка равна нулю. Из условия (7.11) следует, что если j-й вид продукции вошел в оптимальный план, то он в оптимальных оценках неточен, если же j-й вид продукции убыточен, то он не войдет в план, не будет выпуска.
Пример №2. Планирование выпуска продукции пошивочным предприятием
Намечается выпуск двух видов костюмов – мужских и женских.
На женский костюм потребуется 1 метр шерсти, 2 метра лавсана и 1 человеко-день трудозатрат.
На мужской костюм – 3,5 метра шерсти, 0,5 метра лавсана и 1 человеко-день трудозатрат.
Всего имеется 300 метров шерсти, 240 метров лавсана и 150 человеко-дней трудозатрат.
Требуется определить оптимальное число костюмов каждого вида, обеспечивающее максимальную прибыль предприятию, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского 20 денежных единиц. При этом следует иметь ввиду, что необходимо сшить не менее 60 мужских костюмов и обеспечить прибыль не менее 1400 денежных единиц.
Модель задачи:
Введем обозначения:
Х1 и Х2 – число соответственно женских и мужских костюмов. Прибыль от реализации женских костюмов составляет 10Х1, а от реализации мужских костюмов 20Х2, то есть необходимо максимизировать целевую функцию f(x)=10Х1+20Х2šmax.
Ограничения задачи имеют вид:
Х1 +3.5Х2 ≤350
2Х1 +0.5Х2 ≤240
Х1 +Х2 ≤ 150
10Х1 +20Х2 ≥1400
Х2 ≥ 60, Х1,Х2 ≥0
1. Необходимо привести все неравенства системы ограничений исходной задачи к одному виду: если в исходной задаче требуется найти максимум линейной формы, то все неравенства системы ограничений необходимо привести к виду «≤».
Поэтому неравенства, в которых данное требование не выполняется, следует умножить на (-1), в результате получим:
Х 2 ≥60 - Х 2 ≤60
10Х1+20Х2 ≥1400 -10Х1-20Х 2 ≤-1400
2. Выписываем матрицу А коэффициентов при переменных исходной задачи и транспонируем ее:
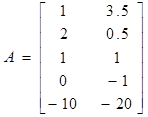

3. Составить систему ограничений двойственной задачи, для чего коэффициенты при переменных взять компоненты транспортированной матрицы Ат:
Y1 +2 Y2 + Y3 - 10Y5 ≥10
3.5Y1+0.5 Y2 + Y3 – Y4 -20Y5 ≥ 20
Y1, 2, 3, 4, 5 ≥0.
4.Составить линейную форму двойственной задачи, взяв коэффициентами при неизвестных Y свободные члены системы ограничений исходной задачи:
g(Y) =350Y1+240Y2 + 150Y3 – 60Y4 +1400Y5.
Y1 – двойственная оценка ресурса «шерсть», которая может быть «ценой» шерсти;
Y2 – двойственная оценка ресурса «лавсан», которая может быть «ценой» лавсана;
Y3 – двойственная оценка ресурса «трудозатраты», которая может быть «ценой» трудозатрат;
Y4 – двойственная оценка заказа по выпуску женских и мужских костюмов;
Y5 – двойственная оценка задания по прибыли.
В результате решения симплексным методом получим:
Х= (70, 80, 0, 60, 0, 40, 900)
У= (4,0, 6, 0, 0, 0, 0)
f(x) = g(y )=2300.
Таким образом, максимальная прибыль составила 2300 денежных единиц, при производстве 70 женских и 80 мужских костюмов.
Дополнительные переменные х5=0, х6=40, х7=900 показывают, что шерсть и трудовые ресурсы использованы полностью (х3 и х5 =0), лавсана осталось 60 м =х4, плановые задания перевыполнены по числу костюмов х6=40 и по прибыли х7=900. Решение двойственной задачи указывает на дефицитность ресурсов «шерсть» (У1=4) и «трудозатраты» (У3=6).
Пример №3. Размещение производственных заказов
В планируемом периоде необходимо обеспечить производство 300000 однородных новых изделий, которые могут выпускаться на четырех филиалах предприятия. Для освоения этого нового вида изделий нужны определенные капитальные вложения. Разработанные для каждого филиала предприятия проекты освоения нового вида изделия характеризуются величинами единицы продукции удельных капиталовложений и себестоимостью единицы продукции (Табл. 7.2.).
Предположим, что на все филиалы предприятия для освоения 300 тысяч новых изделий может выделить 18 миллионов тенге.
Таблица 7.2.
| Показатель | Филиал предприятия | |||
| 1 | 2 | 3 | 4 | |
| Себестоимость производства изделия, тенге Удельные капиталовложения, тенге | 83 120 | 89 80 | 95 50 | 98 40 |
Необходимо найти такой вариант распределения объемов производства продукции и капитальных вложений по филиалам, при котором суммарная стоимость изделий будет минимальной.
Введем обозначения:
i - номер филиала (i=1,…,4);
Xi – объем выпускаемой продукции в i-ом филиале предприятия;
T – суммарная потребность в изделиях (Т=300000 штук);
K – выделяемые капиталовложения (К=18 млн. тенге);
Ci – себестоимость производства продукции в i-ом филиале;
Ki - удельные капиталовложения на 1 продукции в i-ом филиале.
Экономико-математическая модель задачи имеет следующий вид:
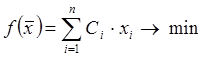
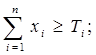

xi ≥ 0 ; i=1,…,n , с учетом имеющихся данных.
f(x)=83Х1 + 89Х2 +95Х3 +98Х4→ min
Х1 + Х2+ Х3+ Х4 ≥300000 штук
12Х1 +80Х2+50Х3+40Х4 ≤ 18 млн. тенге
x1 , x2 , x3 , x4 ≥ 0.
Сформулируем экономико-математическую модель двойственной задачи. Введем обозначения переменных двойственной задачи Y1 и Y2 .
Y1 - двойственная оценка выпускаемой продукции, которая может быть ценой изделия;
Y2 - двойственная оценка капитальных вложений, которая может быть представлена как коэффициент эффективности капитальных вложений.
Экономико-математическая модель двойственной задачи имеет вид:
g(Y)=T.Y1- K.Y2 → max
Y1- K. Y2 ≤ Ci i=1,…,4
Y1 ≥ 0; Y2 ≥ 0.
Целевая функция g(Y) означает, что необходимо максимизировать разность между стоимостью произведенной продукции (T*Y1) и величиной капитальных вложений, соизмеренной во времени с выпуском заданного объема продукции (K*Y2). Разность между ними соответствует суммарному «выигрышу» от вложенных капиталовложений на изготовление 300000 изделий.
Цена продукции Y1 и коэффициент эффективности Y2 взаимосвязаны. Цена одного изделия, выпускаемого в каждом из филиалов, не может быть больше, чем все производственные затраты, включающие в себя в данном случае себестоимость Сi и приведенные к текущим издержкам через коэффициент эффективности капиталовложения Ki*Y1.
Двойственная модель в числах запишется следующим образом:
g(Y)=300000*Y1 –18000000*Y2 → max
Y1 –120* Y2 ≤ 83
Y1 – 80* Y2 ≤ 89
Y1 – 50* Y2 ≤95
Y 1 – 40* Y2 ≤ 98
Вам также может быть полезна лекция "35. Прогнозирование и дизайн белковых структур".
Y1 ≥0; Y2 ≥ 0.
В результате решения получены оптимальные планы:
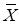 = (0; 100000; 200000; 0);
= (0; 100000; 200000; 0);
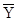 = (105; 0; 2);
= (105; 0; 2);
 = 279 млн.
= 279 млн.
Которые говорят о том, что в первом и четвертом филиалах размещать заказы по выпуску новых изделий невыгодно (x1=0 и x4 =0). Выпуск следует наладить во втором и третьем филиалах. При этом суммарная себестоимость выпускаемых изделий составит 279 миллионов.





















