Векторный способ описания изображения

1.2. Векторный способ описания изображения

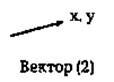
Векторный способ описания основан на построении изображения из геометрических примитивов: точек, отрезков прямых (протяженностей), векторов, дуг окружностей, парабол и подобных им элементов — сплайнов (рис. 2-5). Под сплайном имеют ввиду кривую, гладко соединя­ющую серию фиксированных точек[1].

Каждый такой элемент (геометрический примитив) хранится в памяти компьютера в виде математической формулы. Изображение "расчленено" и состоит из контуров элементов, а замкнутые контуры могут быть "залиты" (заполнены) тем или иным цветом.

Описания, основанные на геометрических примитивах, называют векторными описаниями, а соответствующие им изображения вектор­ными изображениями[2].

Векторные описания имеют следующие основные преимущества:

—компактность (малый размер);

—простоту редактирования (каждый элемент редактируется от­дельно);

—легкость масштабирования (выполняется путем простых математи­ческих операций: параметры примитивов умножаются на коэффициент масштабирования) при неизменном качестве изображения.

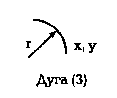
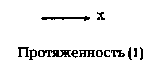
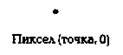
Рекомендуемые материалы

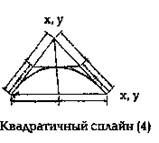
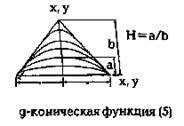
Рис. 2. Геометрические примитивы, используемые для описания изображений

векторным способом, в скобках число степеней свободы.

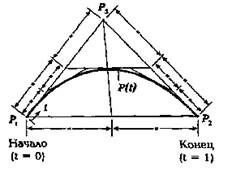
Рис.3. Квадратичный сплайн:

P₁ = (x₁, y₁) – якорная точка, начало контура,

P₂ = (x₂, y₂) – якорная точка, окончание контура,

P₃ = (x₃, y₃) – тангенциальная точка,

P(t)  = (x(t),y(t)) – любая точка кривой 0 ≤ t ≤ 1,

x(t) = x₁(1-t)² + 2x₃(1-t)t + x₂t²,

x(t) = y₁(1-t)² + 2y₃(1-t)t + y₂t²       

Рис.4. g – конические функции: 

P₁ = (x₁, y₁) – якорная точка, начало контура,

P₂ = (x₂, y₂) – якорная точка, окончание контура,

P₃ = (x₃, y₃) – тангенциальная точка,

P(t)  = (x(t),y(t)) – любая точка кривой 0 ≤ t ≤ 1,

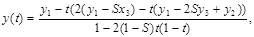H = a / b – крутизна

S = a / (b-a) = H / (1-H)

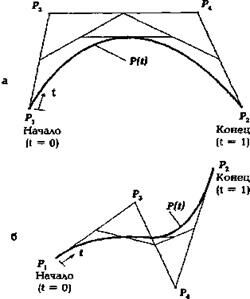
Рис.5. Кубические сплайны (кривые Безье):

P₁ = (x₁, y₁) – якорная точка, начало контура,

P₂ = (x₂, y₂) – якорная точка, окончание контура,

P₃ = (x₃, y₃), P₄ = (x₄, y₄) – тангенциальная точка,

P(t)  = (x(t),y(t)) – любая точка кривой 0 ≤ t ≤ 1,

x(t) = x₁(1-t)³ + 3x₃(1-t)²t +3x₄(1-t)t² + x₂t³,

y(t) = y₁(1-t)³ + 3y₃(1-t)²t +3y₄(1-t)t² + y₂t

Естественным способом вывода (формирования) векторных изобра­жений является векторный способ. Однако, устройств с векторным способом вывода существует очень мало. Это обусловлено тем, что, во-первых, технически сложно реализовать произвольное (в двух коор­динатах) перемещение записывающего, рисующего, печатающего инструмента, а, во-вторых, тем, что создание изображения последовательной прорисовкой геометрических примитивов крайне медленно.

"ТЕМА 4. Моделирование процессов" - тут тоже много полезного для Вас.

К этому классу устройств можно отнести векторные дисплеи, а среди принтеров только:

—графопостроители (используются для вывода чертежей в строительстве и архитектуре),

—перьевые, режущие или универсальные со сменным инструментом плоттеры (применяются в первом варианте как и графопостроители, во втором — для оформления табличек, вывесок и т. п., например, в наружной рекламе).

Векторно описанные изображения очень легко преобразуются в раст­ровые, и, наоборот, практически невозможно осуществить экспорт изображения из растрового формата в векторный.

[1] Исходное значение термина "сплайн" — это тонкие доски, вставляемые между парами гвоздей в палубе парусного корабля, чтобы получить плавные изгибы между фиксированными точками.

[2] Более точным было бы применение этого термина к изображениям, состоящим из отрезков, но не из кривых.