Синтаксический анализ
4. Лекция: Синтаксический анализ
В данной лекции рассматривается понятие синтаксического анализа. Приводятся определения понятий упорядоченного графа, дерева вывода, автомата с магазинной памятью и его конфигурации. Приведены примеры задач, алгоритмов и доказательства теорем синтаксического анализа. 


Контекстно-свободные грамматики и автоматы с магазинной памятью
Пусть G = (N, T, P, S) - КС-грамматика. Введем несколько важных понятий и определений.
Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого левого нетерминала, называется левосторонним. Если S * u в процессе левостороннего вывода, то u - левая сентенциальная форма. Аналогично определим правосторонний вывод. Обозначим шаги левого (правого) вывода
* u в процессе левостороннего вывода, то u - левая сентенциальная форма. Аналогично определим правосторонний вывод. Обозначим шаги левого (правого) вывода  l (
l ( r).
r).
Упорядоченным графом называется пара (V,E), где V есть множество вершин, а E - множество линейно упорядоченных списков дуг, каждый элемент которого имеет вид ((v, v1), (v, v2), ... , (v, vn)). Этот элемент указывает, что из вершины v выходят n дуг, причем первой из них считается дуга, входящая в вершину v1, второй - дуга, входящая в вершинуv2, и т.д.
Упорядоченным помеченным деревом называется упорядоченный граф (V,E), основой которого является дерево и для которого определена функция f : V  F (функция разметки) для некоторого множества F.
F (функция разметки) для некоторого множества F.
Упорядоченное помеченное дерево D называется деревом вывода (или деревом разбора) цепочки w в КС-грамматике G = (N, T, P, S), если выполнены следующие условия:
(1) корень дерева D помечен S;
(2) каждый лист помечен либо  , либо e;
, либо e;
Рекомендуемые материалы
(3) каждая внутренняя вершина помечена нетерминалом  ;
;
(4) если X - нетерминал, которым помечена внутренняя вершина и X1, ... , Xn - метки ее прямых потомков в указанном порядке, то X  X1 ... Xk - правило из множества P;
X1 ... Xk - правило из множества P;
(5) Цепочка, составленная из выписанных слева направо меток листьев, равна w.
Процесс определения принадлежности данной строки языку, порождаемому данной грамматикой, и, в случае указанной принадлежности, построение дерева разбора для этой строки, называется синтаксическим анализом. Можно говорить о восстановлении дерева вывода (в частности, правостороннего или левостороннего) для строки, принадлежащей языку. По восстановленному выводу можно строить дерево разбора.
Грамматика G называется неоднозначной, если существует цепочка w, для которой имеется два или более различных деревьев вывода в G.
Грамматика G называется леворекурсивной, если в ней имеется нетерминал A такой, что для некоторой цепочки R существует вывод A  + A
+ A .
.
Автомат с магазинной памятью (МП-автомат) - это семерка M = (Q, T, Γ, D, q0, Z0, F), где
(1) Q - конечное множество состояний, представляющих всевозможные состояния управляющего устройства;
(2) T - конечный входной алфавит;
(3) Γ - конечный алфавит магазинных символов;
(4) D - отображение множества Q x (T  {e}) x Γ в множество конечных подмножеств Q x Γ*, называемое функцией переходов;
{e}) x Γ в множество конечных подмножеств Q x Γ*, называемое функцией переходов;
(5)  - начальное состояние управляющего устройства;
- начальное состояние управляющего устройства;
(6)  - символ, находящийся в магазине в начальный момент (начальный символ магазина);
- символ, находящийся в магазине в начальный момент (начальный символ магазина);
(7)  - множество заключительных состояний.
- множество заключительных состояний.
Конфигурация МП-автомата - это тройка (q, w, u), где
(1)  - текущее состояние управляющего устройства;
- текущее состояние управляющего устройства;
(2)  - непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
- непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
(3)  - содержимое магазина; самый левый символ цепочки u считается верхним символом магазина; если u = e, то магазин считается пустым.
- содержимое магазина; самый левый символ цепочки u считается верхним символом магазина; если u = e, то магазин считается пустым.
Такт работы МП-автомата M будем представлять в виде бинарного отношения  , определенного на конфигурациях.
, определенного на конфигурациях.
Будем писать
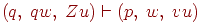
если множество D(q, a, Z) содержит (p, v), где  и
и  (верхушка магазина слева).
(верхушка магазина слева).
Начальной конфигурацией МП-автомата M называется конфигурация вида (q0, w, Z0), где  , то есть управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z0.
, то есть управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z0.
>Заключительной конфигурацией называется конфигурация вида (q, e, u), где  , то есть управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана.
, то есть управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана.
Введем транзитивное и рефлексивно-транзитивное замыкание отношения  , а также его степень k > 0 (обозначаемые
, а также его степень k > 0 (обозначаемые  ,
,  и
и  соответственно).
соответственно).
Говорят, что цепочка w допускается МП-автоматом M, если  для некоторых
для некоторых  и
и  .
.
Множество всех цепочек, допускаемых автоматом M называется языком, допускаемым (распознаваемым, определяемым) автоматом M (обозначается L(M)).
Пример 4.1. Рассмотрим МП-автомат
M = ({q0, q1, q2}, {a, b}, {Z, a, b}, D, q0, Z, {q2}),
у которого функция переходов D содержит элементы:
D(q0, a, Z) = {(q0, aZ)},
D(q0, b, Z) = {(q0, bZ)},
D(q0, a, a) = {(q0, aa), {q1, e)},
D(q0, a, b) = {(q0, ab)},
D(q0, b, a) = {(q0, ba)},
D(q0, b, b) = {(q0, bb), (q1, e)},
D(q1, a, a) = {(q1, e)},
D(q1, b, b) = {(q1, e)},
D(q1, e, Z) = {(q2, e)}.
Нетрудно показать, что  , где wR обозначает обращение ("переворачивание") цепочки w.
, где wR обозначает обращение ("переворачивание") цепочки w.
Иногда допустимость определяют несколько иначе: цепочка w допускается МП-автоматом M, если  для некоторого
для некоторого  . В таком случае говорят, что автомат допускает цепочку опустошением магазина. Эти определения эквивалентны, ибо справедлива
. В таком случае говорят, что автомат допускает цепочку опустошением магазина. Эти определения эквивалентны, ибо справедлива
Теорема 4.1. Язык допускается МП-автоматом тогда и только тогда, когда он допускается (некоторым другим автоматом) опустошением магазина.
Доказательство. Пусть L = L(M) для некоторого МП- автомата M = (Q, T, Γ, D, q0, Z0, F). Построим новый МП- автомат M', допускающий тот же язык опустошением магазина.
Пусть  , где функция переходов D' определена следующим образом:
, где функция переходов D' определена следующим образом:
- Если
![(r, u) in D(q, a, Z)]() , то
, то ![(r, u) in D'(q, a, Z)]() для всех
для всех ![q in Q, a in T cup {e}]() и
и ![Z in Gamma]() (моделирование М),
(моделирование М), ![D'(q'_0 , e, Z'_0) = {(q_0, Z_0 Z'_0 )}]() (начало работы),
(начало работы),- Для всех
![q in F]() и
и ![Z in Gamma cup {Z'_0}]() множество D'(q, e, Z) содержит (qe, e) (переход в состояние сокращения магазина без продвижения),
множество D'(q, e, Z) содержит (qe, e) (переход в состояние сокращения магазина без продвижения), - D'(qe, e, Z) = {(qe, e)} для всех
![Z in Gamma cup {Z'_0}]() , (сокращение магазина).
, (сокращение магазина).
Автомат сначала переходит в конфигурацию  соответственно определению D' в п.2, затем в
соответственно определению D' в п.2, затем в  ,
,
 соответственно п.1, затем в
соответственно п.1, затем в  соответственно п.3, затем в (qe, e, e) соответственно п.4. Нетрудно показать по индукции, что
соответственно п.3, затем в (qe, e, e) соответственно п.4. Нетрудно показать по индукции, что  (где
(где  ) выполняется для автомата M тогда и только тогда, когда
) выполняется для автомата M тогда и только тогда, когда  выполняется для автомата M'. Поэтому L(M) = L', где L' - язык, допускаемый автоматом M' опустошением магазина.
выполняется для автомата M'. Поэтому L(M) = L', где L' - язык, допускаемый автоматом M' опустошением магазина.
Обратно, пусть M = (Q, T, Γ, D, q0, Z0,  ) - МП - автомат, допускающий опустошением магазина язык L. Построим автомат M', допускающий тот же язык по заключительному состоянию.
) - МП - автомат, допускающий опустошением магазина язык L. Построим автомат M', допускающий тот же язык по заключительному состоянию.
Пусть  , где D' определяется следующим образом:
, где D' определяется следующим образом:
![D'(q'_0 , e, Z'_0) = {(q_0, Z_0Z'_0 )}]() - переход в "режим M",
- переход в "режим M",- Для каждого
![q in Q, ain T cup {e}, и Z in Gamma]() определим
определим ![D'(q, a, Z) = D(q, a, Z)]() - работа в "режиме M" ,
- работа в "режиме M" , - Для всех
![q in Q, (q_f , e) in D'(q, e, Z'_0)]() - переход в заключительное состояние.
- переход в заключительное состояние.
Нетрудно показать по индукции, что L = L(M'). Одним из важнейших результатов теории контекстно-свободных языков является доказательство эквивалентности МП-автоматов и КС-грамматик.
Теорема 4.2. Язык является контекстно-свободным тогда и только тогда, когда он допускается МП-авто- матом.
Доказательство. Пусть G = (N, T, P, S) - КС-граммати- ка. Построим МП-автомат, допускающий язык L(G) опустошением магазина.
Пусть M = ({q}, T, N  T, D, q, S,
T, D, q, S,  ), где D определяется следующим образом:
), где D определяется следующим образом:
- Если
![A rightarrow u in P]() , то
, то ![(q, u) in D(q, e, A)]() ,
, - D(q, a, a) = {(q, e)} для всех
![a in T]() .
.
Фактически, этот МП-автомат в точности моделирует все возможные выводы в грамматике G. Нетрудно показать по индукции, что для любой цепочки  вывод S
вывод S  +w в грамматике G существует тогда и только тогда, когда существует последовательность тактов
+w в грамматике G существует тогда и только тогда, когда существует последовательность тактов  автомата M.
автомата M.
Наоборот, пусть дан M = (Q, T, Γ , D, q0, Z0,  ) - МП- автомат, допускающий опустошением магазина язык L.
) - МП- автомат, допускающий опустошением магазина язык L.
Построим грамматику G, порождающую язык L.
Пусть ![G = ({ [qZr] mid q, r in Q, Z in Gamma } cup {S}, T, P, S)](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/66-4-sintaksicheskiy-analiz.png) , где P состоит из правил следующего вида:
, где P состоит из правил следующего вида:
![S rightarrow [q_0Z_0q] in P]() для всех
для всех ![q in Q]() .
.- Если
![(r, e) in D(q, a, Z), ; text{то} ; [qZr] rightarrow a in P, a in T cup {e}]() ,
, - Если
![(r, X_1 ldots X_k) in D(q, a, Z), k geq 1]() , то
, то
![begin{align*} text{$[qZs_k] rightarrow a[rX_1s_1][s_1X_2s_2] ldots [s_{k-1}X_ks_k]$} \ text{для любого набора $s_1, s_2, ldots , s_k$ состояний из $Q$,} end{align*}](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/71-4-sintaksicheskiy-analiz.png)
Нетерминалы и правила вывода грамматики определены так, что работе автомата M при обработке цепочки w соответствует левосторонний вывод w в грамматике G.
Индукцией по числу шагов вывода в G или числу тактов M нетрудно показать, что  тогда и только тогда, когда [qAp]
тогда и только тогда, когда [qAp]  + w.
+ w.
Тогда, если  , то S
, то S  [q0Z0q]
[q0Z0q]  + w для некоторого
+ w для некоторого  . Следовательно,
. Следовательно,  и поэтому
и поэтому  . Аналогично, если
. Аналогично, если  , то
, то  . Значит, S
. Значит, S  [q0Z0q]
[q0Z0q]  + w, и поэтому
+ w, и поэтому  .
.
МП-автомат M = (Q, T, Γ, D, q0, Z0, F) называется детерминированным (ДМП-автоматом), если выполнены два следующих условия:
(1) Множество D(q, a, Z) содержит не более одного элемента для любых  ;
;
(2) Если D(q, e, Z) 
 , то D(q, a, Z) =
, то D(q, a, Z) =  для всех
для всех 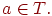
Допускаемый ДМП-автоматом язык называется детерминированным КС-языком.
Так как функция переходов ДМП-автомата содержит не более одного элемента для любой тройки аргументов, мы будем пользоваться записью D(q, a, Z) = (p, u) для обозначения D(q, a, Z) = {(p, u)}.
Пример 4.2. Рассмотрим ДМП-автомат
M = ({q0, q1, q2}, {a, b, c}, {Z, a, b}, D, q0, Z, {q2}),
функция переходов которого определяется следующим образом:
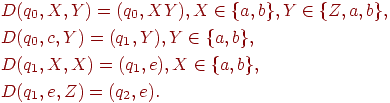
Нетрудно показать, что этот детерминированный МП-автомат допускает язык  .
.
К сожалению, ДМП-автоматы имеют меньшую распознавательную способность, чем МП-автоматы. Доказано, в частности, что существуют КС-языки, не являющиеся детерминированными КС-языками (таковым, например, является язык из примера 4.1).
Рассмотрим еще один важный вид МП-автомата.
Расширенным автоматом с магазинной памятью назовем семерку M = (Q, T, Γ , D, q0, Z0, F), где смысл всех символов тот же, что и для обычного МП-автомата, кроме D, представляющего собой отображение конечного подмножества множества Q x(T  {e}) x Γ* во множество конечных подмножеств множества Q x Γ*. Все остальные определения (конфигурации, такта, допустимости) для расширенного МП-автомата остаются такими же, как для обычного.
{e}) x Γ* во множество конечных подмножеств множества Q x Γ*. Все остальные определения (конфигурации, такта, допустимости) для расширенного МП-автомата остаются такими же, как для обычного.
Теорема 4.3. Пусть M = (Q, T, Γ, D, q0, Z0, F) - расширенный МП-автомат. Тогда существует МП- автомат M', такой, что L(M') = L(M).
Расширенный МП-автомат M = (Q, T, Γ, D, q0, Z0, F) называется детерминированным, если выполнены следующие условия:
(1) Множество D(q, a, u) содержит не более одного элемента для любых  ,
,
(2) Если D(q, a, u) 
 , D(q, a, v)
, D(q, a, v) 
 и u
и u  v, то не существует цепочки x такой, что u = vx или v = ux,
v, то не существует цепочки x такой, что u = vx или v = ux,
(3) Если D(q, a, u) 
 , D(q, e, v)
, D(q, e, v) 
 , то не существует цепочки x такой, что u = vx или v = ux.
, то не существует цепочки x такой, что u = vx или v = ux.
Теорема 4.4. Пусть M = (Q, T, Γ, D, q0, Z0, F) - расширенный ДМП-автомат. Тогда существует ДМП- автомат M', такой, что L(M') = L(M).
ДМП-автомат и расширенный ДМП-автомат лежат в основе рассматриваемых далее в этой главе, соответственно, LL- и LR-анализаторов.
Определение. Говорят, что КС-грамматика находится в нормальной форме Хомского, если каждое правило имеет вид:
(1) либо A  BC, A, B, C - нетерминалы,
BC, A, B, C - нетерминалы,
(2) либо A  a, a - терминал,
a, a - терминал,
(3) либо S  e и в этом случае S - не встречается в правых частях правил.
e и в этом случае S - не встречается в правых частях правил.
Утверждение. Любую КС-грамматику можно преобразовать в эквивалентную ей в нормальной форме Хомского.
Утверждение. Если КС-грамматика находится в нормальной форме Хомского, тогда для любой цепочки  , если
, если  и m - высота дерева вывода с кроной
и m - высота дерева вывода с кроной  , |
, | |
|  2m-1.
2m-1.
Теорема 4.5. (Лемма о разрастании для контекстно- свободных языков). Для любого КС-языка L существуют такие целые l и k, что любая цепочка  , представима в виде R = uvwxy, где
, представима в виде R = uvwxy, где
(1) |vwx|  k
k
(2) vx  e
e
(3)  для любого i
для любого i  0.
0.
Доказательство. Пусть L = L(G), где G = (N, Σ, P, S) - контекстно- свободная грамматика в нормальной форме Хомского. Обозначим через n число нетерминалов, т.е. n = |N|, и рассмотрим l = 2n и k = 2n+1.
Для доказательства того, что l и k удовлетворяют условию теоремы, рассмотрим произвольную цепочку  , для которой |
, для которой | | > l = 2n. В силу Утверждения получаем, что высота дерева с кроной
| > l = 2n. В силу Утверждения получаем, что высота дерева с кроной  больше n + 1 и есть путь по дереву (обозначим его через P), который проходит более чем через n + 1 вершин. Отсюда по определению дерева вывода имеем, что P содержит более n вершин, помеченных нетерминалами. Таким образом, существует нетерминал, который метит не менее двух вершин пути P. Среди всех таких нетерминалов пусть A - такой, что его вхождение, ближайшее к листу, не содержит других нетерминалов, обладающих этим свойством (если бы это было не так, то выбрали бы этот другой). Пусть q - вхождение A, ближайшее к листу, p - расположенное выше. Представим крону
больше n + 1 и есть путь по дереву (обозначим его через P), который проходит более чем через n + 1 вершин. Отсюда по определению дерева вывода имеем, что P содержит более n вершин, помеченных нетерминалами. Таким образом, существует нетерминал, который метит не менее двух вершин пути P. Среди всех таких нетерминалов пусть A - такой, что его вхождение, ближайшее к листу, не содержит других нетерминалов, обладающих этим свойством (если бы это было не так, то выбрали бы этот другой). Пусть q - вхождение A, ближайшее к листу, p - расположенное выше. Представим крону  в виде uvwxy, где w - крона поддерева D1 с корнем q и vwx - крона поддерева D2 с корнем p. Тогда высота поддерева D2 не более (n - 1) + 2 + 1 = n + 2, так что |vwz|
в виде uvwxy, где w - крона поддерева D1 с корнем q и vwx - крона поддерева D2 с корнем p. Тогда высота поддерева D2 не более (n - 1) + 2 + 1 = n + 2, так что |vwz|  2n+1.
2n+1.
Также очевидно, что vx  e, поскольку в силу определения нормальной формы Хомского p имеет двух сыновей, помеченных нетерминалами, из которых не выводится пустая цепочка.
e, поскольку в силу определения нормальной формы Хомского p имеет двух сыновей, помеченных нетерминалами, из которых не выводится пустая цепочка.
Кроме того, S  * u Ay
* u Ay  * uvAxy
* uvAxy  * uvwxy, а также A
* uvwxy, а также A  * vAx
* vAx  * vwx. Отсюда получаем A
* vwx. Отсюда получаем A  * viwxi для всех i
* viwxi для всех i  0 и S
0 и S  * uviwxiy для всех i
* uviwxiy для всех i  0.
0.
Пример. Покажем, что язык L = {anbncn|n 1} не является контекстно-свободным языком.
1} не является контекстно-свободным языком.
Если бы он был КС-языком, то мы взяли бы константу k, которая определяется в лемме о разрастании. Пусть z = akbkck. Тогда z = uvwxy. Так как |vwx|  k, то в цепочке vwx не могут быть вхождения каждого из символов a, b и c. Таким образом, цепочка uwy, которая по лемме о разрастании принадлежит L, содержит либо k символов a, либо k символов c. Но она не может иметь k вхождений каждого из символов a, b и c, потому, что |uwy| < 3k. Значит, вхождений какого-то из этих символов в uwy больше, чем другого и, следовательно, uwy
k, то в цепочке vwx не могут быть вхождения каждого из символов a, b и c. Таким образом, цепочка uwy, которая по лемме о разрастании принадлежит L, содержит либо k символов a, либо k символов c. Но она не может иметь k вхождений каждого из символов a, b и c, потому, что |uwy| < 3k. Значит, вхождений какого-то из этих символов в uwy больше, чем другого и, следовательно, uwy  L. Полученное противоречие позволяет заключить, что L - не КС-язык.
L. Полученное противоречие позволяет заключить, что L - не КС-язык.
Преобразования КС-грамматик
Рассмотрим ряд преобразований, позволяющих "улучшить" вид контекстно-свободной грамматики без изменения порождаемого ею языка.
Назовем символ  недостижимым в КС- грамматике G = (N, T, P, S), если X не появляется ни в одной выводимой цепочке этой грамматики. Иными словами, символ X является недостижимым, если в G не существует вывода S
недостижимым в КС- грамматике G = (N, T, P, S), если X не появляется ни в одной выводимой цепочке этой грамматики. Иными словами, символ X является недостижимым, если в G не существует вывода S  *
*  Xβ ни для каких
Xβ ни для каких  .
.
Назовем символ  несводимым (бесплодным) в той же грамматике, если в ней не существует вывода вида X
несводимым (бесплодным) в той же грамматике, если в ней не существует вывода вида X  * xwy, где w, x, y принадлежат T*.
* xwy, где w, x, y принадлежат T*.
Очевидно, что каждый недостижимый и/или несводимый символ является бесполезным, как и все правила, его содержащие.
При внимательном изучении вышеприведенных определений становится понятным, что а) целесообразно искать не непосредственно сами недостижимые (или несводимые) символы, а последовательно определять множество достижимых (или сводимых) символов, начиная с тех, которые по определению являются достижимыми (аксиома) и сводимыми (терминалы) - все остальные символы оказываются бесполезными, б) одновременное определение достижимых и сводимых символов невозможно, так как соответствующие процессы идут в противоположных направлениях (от корня к листьям и наоборот).
Алгоритм 4.1. Устранение недостижимых символов.
Вход. КС-грамматика G = (N, T, P, S).
Выход. КС-грамматика G' = (N', T', P', S) без недостижимых символов, такая, что L(G') = L(G).
Метод. Выполнить шаги 1-4:
(1) Положить V0 = {S} и i = 1,
(2) Положить Vi = {X | в P есть A 
 Xβ и
Xβ и  ,
,
(3) Если Vi  Vi-1, положить i = i + 1 и перейти к шагу 2, в противном случае перейти к шагу 4,
Vi-1, положить i = i + 1 и перейти к шагу 2, в противном случае перейти к шагу 4,
(4) Положить N' = Vi  N, T' = Vi
N, T' = Vi  T. Включить в P' все правила из P, содержащие только символы из Vi.
T. Включить в P' все правила из P, содержащие только символы из Vi.
Алгоритм 4.2. Устранение несводимых символов.
Вход. КС-грамматика G = (N, T, P, S).
Выход. КС-грамматика G' = (N', T', P', S) без несводимых символов, такая, что L(G') = L(G).
Метод. Выполнить шаги 1-4:
(1) Положить N' = T и i = 1,
(2) Положить  ,
,
(3) Если Ni  Ni-1, положить i = i + 1 и перейти к шагу 2, в противном случае положить Ne = Ni и перейти к шагу 4,
Ni-1, положить i = i + 1 и перейти к шагу 2, в противном случае положить Ne = Ni и перейти к шагу 4,
(4) Положить G1 = ((N  Ne)
Ne)  {S}, T, P1, S), где P1 состоит из правил множества P, содержащих только символы из Ne
{S}, T, P1, S), где P1 состоит из правил множества P, содержащих только символы из Ne  T,
T,
Чтобы устранить все бесполезные символы, необходимо применить к исходной грамматике сначала Алгоритм 4.2, а затем Алгоритм 4.1.
Пример. Все символы следующей грамматики
S  AS | b
AS | b
A  AB
AB
B  a
a
являются достижимыми. Поэтому нарушение предложенного порядка применения к ней алгоритмов приведет лишь к частичному решению задачи.
КС-грамматика без бесполезных символов называется приведенной. Легко видеть, что для любой КС-грамматики существует эквивалентная приведенная. В дальнейшем будем предполагать, что все рассматривамые грамматики - приведенные.
Алгоритм Кока-Янгера-Касами
Приведем алгоритм синтаксического анализа, применимый для любой грамматики в нормальной форме Хомского
Алгоритм Кока-Янгера-Касами
Вход. КС-грамматика G = (N, T, P, S) в нормальной форме Хомского и входная цепочка  .
.
Выход. Таблица разбора Tab для w такая, что  тогда и только тогда, когда A
тогда и только тогда, когда A  + aiai+1 ... ai+j-1.
+ aiai+1 ... ai+j-1.
Метод.
(1) Положить  для каждого i. Так что, если
для каждого i. Так что, если  , то A
, то A  + ai.
+ ai.
(2) Пусть tij вычислено для 1 i
i n и 1
n и 1 j' < j. Положим tij = {A| для некоторого 1
j' < j. Положим tij = {A| для некоторого 1  k < j правило
k < j правило  .
.
Так как 1  k < j, то k < j и j - k < j. Так что tik и ti+k,j-k вычисляются раньше, чем tij . Если
k < j, то k < j и j - k < j. Так что tik и ti+k,j-k вычисляются раньше, чем tij . Если  , то A
, то A  BC
BC  + ai ai+k-1 C
+ ai ai+k-1 C  + aI ... ai+k-1ai+k ... ai+j-1.
+ aI ... ai+k-1ai+k ... ai+j-1.
(3) Повторять шаг 2 до тех пор, пока не станут известны tij для всех 1  i
i  n и 1
n и 1  j
j  n-i+1.
n-i+1.
Алгоритм нахождения левого разбора по таблице разбора Tab.
Вход. КС-грамматика G = (N, T, P, S) в нормальной форме Хомского с правилами, занумерованными от 1 до p, входная цепочка  и таблица разбора Tab.
и таблица разбора Tab.
Выход. Левый разбор цепочки w или сигнал ошибка.
Метод. Процедура gen(i, j, A):
(1) Если j = 1 и A  ai = pm, выдать m.
ai = pm, выдать m.
(2) Пусть j > 1 и k - наименьшее из чисел от 1 до j-1, для которых существует  и правило pm = A
и правило pm = A  BC. Выдать m и выполнить gen(i, k, B), затем gen(i + k, j - k, C).
BC. Выдать m и выполнить gen(i, k, B), затем gen(i + k, j - k, C).
Выполнить gen(1, n, S), если  , иначе ошибка.
, иначе ошибка.
Разбор сверху-вниз (предсказывающий разбор)
Алгоритм разбора сверху-вниз
Пусть дана КС-грамматика G = (N; T; P; S). Рассмотрим разбор сверху-вниз (предсказывающий разбор) для грамматики G.
Главная задача предсказывающего разбора - определение правила вывода, которое нужно применить к нетерминалу. Процесс предсказывающего разбора с точки зрения построения дерева разбора проиллюстрирован на рис. 4.1
Фрагменты недостроенного дерева соответствуют сентенциальным формам. Вначале дерево состоит только из одной вершины, соответствующей аксиоме S. В этот момент по первому символу входной цепочки предсказывающий анализатор должен определить правило S  X1X2 ... ; которое должно быть применено к S. Затем необходимо определить правило, которое должно быть применено к X1, и т.д., до тех пор, пока в процессе такого построения сентенциальной формы, соответствующей левому выводу, не будет применено правило Y
X1X2 ... ; которое должно быть применено к S. Затем необходимо определить правило, которое должно быть применено к X1, и т.д., до тех пор, пока в процессе такого построения сентенциальной формы, соответствующей левому выводу, не будет применено правило Y  a ... : Этот процесс затем применяется для следующего самого левого нетерминального символа сентенциальной формы.
a ... : Этот процесс затем применяется для следующего самого левого нетерминального символа сентенциальной формы.
На рис. 4.2 условно показана структура предсказывающего анализатора, который определяет
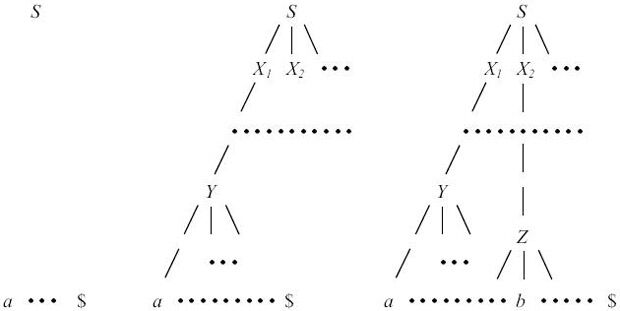
Рис. 4.1.
очередное правило с помощью таблицы. Такую таблицу можно построить и непосредственно по грамматике. Таблично-управляемый предсказывающий анализатор имеет входную ленту, управляющее устройство (программу), таблицу анализа, магазин (стек) и выходную ленту. Входная лента содержит анализируемую строку, заканчивающуюся символом $ - маркером конца строки. Выходная лента содержит последовательность примененных правил вывода.
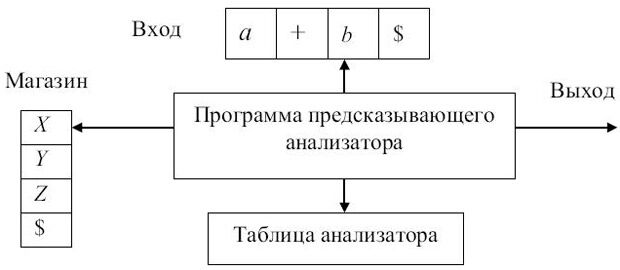
Рис. 4.2.
Таблица анализа - это двумерный массив M[A; a], где A - нетерминал, и a - терминал или символ $. Значением M[A; a] может быть некоторое правило грамматики или элемент "ошибка".
Магазин может содержать последовательность символов грамматики с $ на дне. В начальный момент магазин содержит только начальный символ грамматики на верхушке и $ на дне.
Анализатор работает следующим образом. Вначале анализатор находится в конфигурации, в которой магазин содержит S$, на входной ленте w$ (w - анализируемая цепочка), выходная лента пуста. На каждом такте анализатор рассматривает X - символ на верхушке магазина и a - текущий входной символ. Эти два символа определяют действия анализатора. Имеются следующие возможности.
- Если X=a=$, анализатор останавливается, сообщает об успешном окончании разбора и выдает содержимое выходной ленты.
- Если X= a
![]() $, анализатор удаляет X из магазина и продвигает указатель входа на следующий входной символ.
$, анализатор удаляет X из магазина и продвигает указатель входа на следующий входной символ. - Если X - терминал, и X
![]() a, то анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
a, то анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку. - Если X - нетерминал, анализатор заглядывает в таблицу M[X; a]. Возможны два случая:
- Значением M[X; a] является правило для X. В этом случае анализатор заменяет X на верхушке магазина на правую часть данного правила, а само правило помещает на выходную ленту. Указатель входа не передвигается.
- Значением M[X; a] является "ошибка". В этом случае анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку. Работа анализатора может быть задана следующей программой:
Поместить '$', затем S в магазин;
do
{X=верхний символ магазина;
if (X - терминал)
if (X==InSym)
{удалить X из магазина;
InSym=очередной символ;
}
else {error(); break;}
else if (X - нетерминал)
if (M[X,InSym]=="X->Y1Y2...Yk")
{удалить X из магазина;
поместить Yk,Yk-1,...Y1 в магазин
(Y1 на верхушку);
вывести правило X->Y1Y2...Yk;
}
else {error(); break;} /*вход таблицы M пуст*/
}
while (X!='$'); /*магазин пуст*/
if (InSym != '$') error(); /*Не вся строка прочитана*/
Пример 4.3. Рассмотрим грамматику арифметических выражений G=({E; E', T, T', F}, {id, +, *, (, )}, P, E) с правилами:

В таблица 4.3 приведена предсказывающего анализатора для этой грамматики. Пустые клетки таблицы соответствуют элементу "ошибка".
| Таблица 4.3. | |||||||
| Нетерминал | Входной символ | ||||||
| id | + | * | ( | ) | $ | ||
| E | E | E | |||||
| E' | E' | E' | E' | ||||
| T | T | T | |||||
| T' | T' | T' | T' | T' | |||
| F | F | F |
При разборе входной цепочки id + id * id$ анализатор совершает последовательность шагов, изображенную в таблица 4.4. Заметим, что анализатор осуществляет в точности левый вывод. Если за уже просмотренными входными символами поместить символы грамматики в магазине, то можно получить в точности левые сентенциальные формы вывода. Дерево разбора для этой цепочки приведено на рис. рис. 4.3.
| Таблица 4.4. | ||
| Магазин | Вход | Выход |
| E$ | id + id * id$ | |
| TE'$ | id + id * id$ | E |
| FT'E'$ | id + id * id$ | T |
| id T'E'$ | id + id * id$ | F |
| T'E'$ | +id * id$ | |
| E'$ | +id * id$ | T' |
| +TE'$ | +id * id$ | E' |
| TE'$ | id * id$ | |
| FT'E'$ | id * id$ | T |
| id T'E'$ | id * id$ | F |
| T'E'$ | *id$ | |
| *F'T'E'$ | *id$ | T' |
| FT'E'$ | id$ | |
| id T'E'$ | id$ | F |
| T'E'$ | $ | |
| E'$ | $ | T' |
| $ | $ | E' |
Функции FIRST и FOLLOW
При построении таблицы предсказывающего анализатора нам потребуются две функции - FIRST и FOLLOW.
Пусть G = (N, T, P, S) - КС-грамматика. Для  - произвольной цепочки, состоящей из символов грамматики, определим FIRST(
- произвольной цепочки, состоящей из символов грамматики, определим FIRST( ) как множество терминалов, с которых
) как множество терминалов, с которых
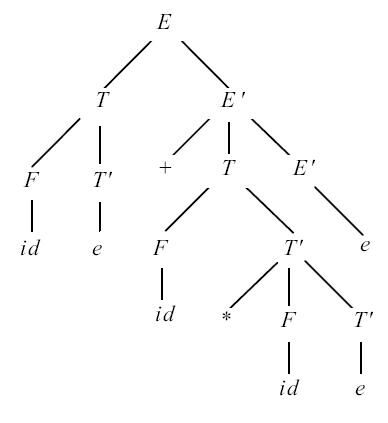
Рис. 4.3.
начинаются строки, выводимые из  . Если
. Если 
 * e, то e также принадлежит FIRST(
* e, то e также принадлежит FIRST( ).
).
Определим FOLLOW(A) для нетерминала A как множество терминалов a, которые могут появиться непосредственно справа от A в некоторой сентенциальной форме грамматики, то есть множество терминалов a таких, что существует вывод вида S  *
*  Aaβ для некоторых
Aaβ для некоторых  . Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
. Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
Рассмотрим алгоритмы вычисления функции FIRST.
Алгоритм 4.3. Вычисление FIRST для символов КС- грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X) для каждого символа  .
.
Метод. Выполнить шаги 1-3:
(1) Если X - терминал, то положить FIRST(X) = {X}; если X - нетерминал, положить FIRST(X) =  .
.
(2) Если в P имеется правило X  e, то добавить e к FIRST(X).
e, то добавить e к FIRST(X).
(3) Пока ни к какому множеству FIRST(X) нельзя уже будет добавить новые элементы, выполнять:
do { continue = false;
Для каждого нетерминала X
Для каждого правила X  Y1Y2...Yk
Y1Y2...Yk
{i=1; nonstop = true;
while (i  k && nonstop)
k && nonstop)
{добавить FIRST(Yi) n {e} к FIRST(X);
if (Были добавлены новые элементы)
continue = true;
if (e  FIRST (Yi)) nonstop = false;
FIRST (Yi)) nonstop = false;
else i+ = 1;
}
if (nonstop) {добавить e к FIRST(X);
continue = true;
} } }
while (continue);
Алгоритм 4.4. Вычисление FIRST для цепочки.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество  .
.
Метод. Выполнить шаги 1-3:
(1) При помощи алгоритма 4.3. вычислить FIRST(X) для каждого  .
.
(2) Положить FIRST(X1X2 ... Xn) =  .
.
(3)
{i = 1; nonstop = true;
while (i  && nonstop)
&& nonstop)
{добавить FIRST(Xi) n {e} к FIRST(u);
if (e  FIRST(Xi)nonstop = false;
FIRST(Xi)nonstop = false;
else i+ = 1;
}
if (nonstop) {добавить e к FIRST(u);
} }
Рассмотрим алгоритм вычисления функции FOLLOW.
Алгоритм 4.5. Вычисление FOLLOW для нетерминалов грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FOLLOW(X) для каждого символа  .
.
Метод. Выполнить шаги 1-4:
(1) Положить FOLLOW(X) =  для каждого символа
для каждого символа  .
.
(2) Добавить $ к FOLLOW(S).
(3) Если в P eсть правило вывода A 
 Bβ, где
Bβ, где  , то все элементы из FIRST(β), за исключением e, добавить к FOLLOW(B).
, то все элементы из FIRST(β), за исключением e, добавить к FOLLOW(B).
(4) Пока ничего нельзя будет добавить ни к какому множеству FOLLOW(X), выполнять:
если в P есть правило A 
 B или A
B или A 
 Bβ,
Bβ,  , где FIRST(β) содержит e (β
, где FIRST(β) содержит e (β *e), то все элементы из FOLLOW(A) добавить к FOLLOW(B).
*e), то все элементы из FOLLOW(A) добавить к FOLLOW(B).
Пример 4.4. Рассмотрим грамматику из примера 4.3. Для нее
FIRST(E) = FIRST(T) = FIRST(F) = {(, id}
FIRST(E') = {+, e}
FIRST(T') = {*, e}
FOLLOW(E) = FOLLOW(E') = { ), $}
FOLLOW(T) = FOLLOW(T') = {+, ), $}
FOLLOW(F) = {+, *, ), $}
Например, id и левая скобка добавляются к FIRST(F) на шаге 3 при i = 1, поскольку FIRST(id) = {id} и FIRST("(") = {"("} в соответствии с шагом 1. На шаге 3 при i = 1, в соответствии с правилом вывода T  FT', к FIRST(T) добавляются также id и левая скобка. На шаге 2 в FIRST(E') включается e.
FT', к FIRST(T) добавляются также id и левая скобка. На шаге 2 в FIRST(E') включается e.
Также при вычислении множеств FOLLOW на шаге 2 в FOLLOW(E) включается $. На шаге 3, на основании правила F  (E), к FOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E
(E), к FOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E  TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку
TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку  , они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E
, они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E  TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
Определим теперь функцию FIRSTk(R), где k - натуральное число и  .
.
 либо |w| < k и
либо |w| < k и  , либо
, либо  для некоторого
для некоторого  .
.
Если  , то FIRSTk(
, то FIRSTk( ) = {w}, где w - это первые k символов цепочки
) = {w}, где w - это первые k символов цепочки  при |
при | |
|  k и w =
k и w =  при |
при | | < k.
| < k.
Приведем алгоритм вычисления функции FIRSTk(β), где  .
.
Определение. Пусть Σ - некоторый алфавит. Если L1 и L2 - подмножества Σ*, то положим
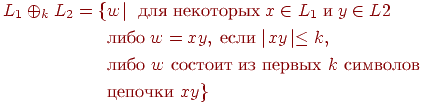
Лемма 4.1. Для любой КС-грамматики G = (N, Σ, P, S) и любых 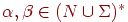
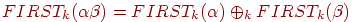
Доказательство оставляем читателю в качестве упражнения.
Aлгоритм 4.6. Вычисление функции FIRSTk( ).
).
Вход. КС-грамматика G = (N, Σ, P, S) и цепочка  .
.
Выход. FIRSTk(β).
Метод. Так как по последней лемме
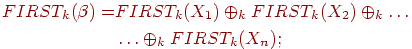
то достаточно показать, как найти FIRSTk(X) для  .
.
Если  , то очевидно, что FIRSTk(X) = {X}.
, то очевидно, что FIRSTk(X) = {X}.
Определим множества Fi(X) для каждого  и возрастающих значений i
и возрастающих значений i  0:
0:
(1) Fi(a) = {a} для всех  и i
и i  0:
0:
(2)  и существует правило A
и существует правило A  x
x из P, для которого либо |x| = k, либо |x| < k и
из P, для которого либо |x| = k, либо |x| < k и  = e}.
= e}.
(3) Допустим, что F0, F1..., Fi-1 уже определены для всех  . Тогда
. Тогда
Fi(A) = Fi-1(A)  {x|A
{x|A  Y1...Yn принадлежит P и
Y1...Yn принадлежит P и 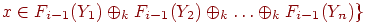
(4) Так как  для всех A и i, то в конце концов мы дойдем до такого i, что Fi-1(A) = Fi(A) для всех
для всех A и i, то в конце концов мы дойдем до такого i, что Fi-1(A) = Fi(A) для всех  . Тогда положим FIRSTk(A) = Fi(A) для этого значения i.
. Тогда положим FIRSTk(A) = Fi(A) для этого значения i.
Конструирование таблицы предсказывающего анализатора
Для конструирования таблицы предсказывающего анализатора по грамматике G может быть использован алгоритм, основанный на следующей идее. Предположим, что A 
 - правило вывода грамматики и
- правило вывода грамматики и  . Тогда анализатор делает развертку A по
. Тогда анализатор делает развертку A по  , если входным символом является a. Трудность возникает, когда
, если входным символом является a. Трудность возникает, когда  = e или
= e или  . В этом случае нужно развернуть A в
. В этом случае нужно развернуть A в  , если текущий входной символ принадлежит FOLLOW(A) или если достигнут $ и
, если текущий входной символ принадлежит FOLLOW(A) или если достигнут $ и  .
.
Алгоритм 4.7. Построение таблицы предсказывающего анализатора.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Таблица M[A; a] предсказывающего анализатора,  .
.
Метод. Для каждого правила вывода A
 грамматики выполнить шаги 1 и 2. После этого выполнить шаг 3.
грамматики выполнить шаги 1 и 2. После этого выполнить шаг 3.
(1) Для каждого терминала a из FIRST(R) добавить A R к M[A; a].
R к M[A; a].
(2) Если  , добавить A
, добавить A  R к M[A; b] для каждого терминала b из FOLLOW(A). Кроме того, если
R к M[A; b] для каждого терминала b из FOLLOW(A). Кроме того, если  и
и  , добавить A
, добавить A 
 к M[A; $].
к M[A; $].
(3) Положить все неопределенные входы равными "ошибка".
Пример 4.5. Применим алгоритм 4.7 к грамматике из примера 4.3. Поскольку FIRST(TE') = FIRST(T) = {(, id }, в соответствии с правилом вывода E  TE' входы M[E, ( ] и M[E, id ] становятся равными E
TE' входы M[E, ( ] и M[E, id ] становятся равными E  TE'.
TE'.
В соответствии с правилом вывода E'  +TE' значение M[E', +] равно E'
+TE' значение M[E', +] равно E'  +TE'. В соответствии с правилом вывода E'
+TE'. В соответствии с правилом вывода E'  e значения M[E', )] и M[E', $] равны E'
e значения M[E', )] и M[E', $] равны E'  e, поскольку FOLLOW(E') = { ), $}.
e, поскольку FOLLOW(E') = { ), $}.
Таблица анализа, построенная по алгоритму 4.7. для этой грамматики, приведена в таблица 4.3.
LL(1)-грамматики
Алгоритм 4.7 построения таблицы предсказывающего анализатора может быть применен к любой КС-грамматике. Однако для некоторых грамматик построенная таблица может иметь неоднозначно определенные входы. Например, нетрудно доказать, что если грамматика леворекурсивна или неоднозначна, таблица будет иметь по крайней мере один неоднозначно определенный вход.
Грамматики, для которых таблица предсказывающего анализатора не имеет неоднозначно определенных входов, называются LL(1)-грамматиками. Предсказывающий анализатор, построенный для LL(1)-грамматики, называется LL(1)-анализатором. Первая буква L в названии связано с тем, что входная цепочка читается слева направо, вторая L означает, что строится левый вывод входной цепочки, 1 - что на каждом шаге для принятия решения используется один символ непрочитанной части входной цепочки.
Доказано, что алгоритм 4.7 для каждой из LL(1)-грам- матик G строит таблицу предсказывающего анализатора, распознающего все цепочки из L(G) и только эти цепочки. Нетрудно доказать также, что если G - LL(1)-грамматика, то L(G) - детерминированный КС-язык.
Справедлив также следующий критерий LL(1)-граммати- ки. Грамматика G = (N, T, P, S) является LL(1)-грамматикой тогда и только тогда, когда для каждой пары правил A 
 , A
, A  β из P
β из P
(то есть правил с одинаковой левой частью) выполняются следующие 2 условия:
(1) 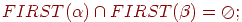
(2) Если  , то FIRST(β)
, то FIRST(β)  FOLLOW(A)=
FOLLOW(A)=  .
.
Язык, для которого существует порождающая LL(1)- грамматика, называют LL(1)-языком. Доказано, что проблема определения, порождает ли грамматика LL-язык, является алгоритмически неразрешимой.
Пример 4.6. Неоднозначная грамматика не является LL(1). Примером может служить следующая грамматика
G = ({S, E}, {if, then, else, a, b}, P, S) с правилами:
S  if E then S | if E then S else S | a
if E then S | if E then S else S | a
E  b
b
Эта грамматика является неоднозначной, что иллюстрируется на рис. 4.4.
LL(k)-грамматики
Определение. КС-грамматика G = (N, Σ, P, S) называется LL(k)-грамматикой для некоторого фиксированного k, если из
(1) 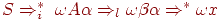
(2)  для которых
для которых
и
FIRSTk(x) = FIRSTk(y), вытекает, что β = γ.
Говоря менее формально, G будет LL(k)- грамматикой, если для данной цепочки  и первых k символов (если они есть), выводящихся из A
и первых k символов (если они есть), выводящихся из A , существует не более одного правила, которое можно применить к A, чтобы получить вывод какой-нибудь терминальной цепочки,
, существует не более одного правила, которое можно применить к A, чтобы получить вывод какой-нибудь терминальной цепочки,
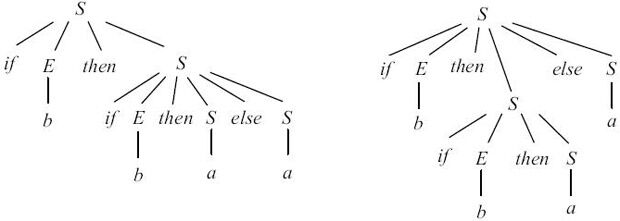
Рис. 4.4.
начинающейся с ω и продолжающейся упомянутыми k терминалами.
Грамматика называется LL(k)-грамматикой, если она LL(k)-грамматика для некоторого k.
Пример 4.7. Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S), где P состоит из правил
S  A | B,
A | B,
A  aAb | 0,
aAb | 0,
B  aBbb | 1.
aBbb | 1.
Здесь L(G) = an0bn | n  0
0  an1b2n | n
an1b2n | n  0. G не является LL(k)-грамматикой ни для какого k. Интуитивно, если мы начинаем с чтения достаточно длинной цепочки, состоящей из символов a, то не знаем, какое из правил S
0. G не является LL(k)-грамматикой ни для какого k. Интуитивно, если мы начинаем с чтения достаточно длинной цепочки, состоящей из символов a, то не знаем, какое из правил S  A и S
A и S  B было применено первым, пока не встретим 0 или 1.
B было применено первым, пока не встретим 0 или 1.
Обращаясь к точному определению LL(k)-грамматики, положим ω =  = e; β = A; γ = B; x = ak0bk и y = ak1b2k. Тогда выводы
= e; β = A; γ = B; x = ak0bk и y = ak1b2k. Тогда выводы
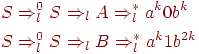
соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение β = γ ложно. Так как k здесь выбрано произвольно, то G не является LL-грамматикой.
Следствия определения LL(k)- грамматики
Теорема 4.6. КС-грамматика G = (N, Σ, P, S) является LL(k)-грамматикой тогда и только тогда, когда для двух различных правил A  β и A
β и A  γ из Р пересечение FIRSTk(β
γ из Р пересечение FIRSTk(β )
)  FIRSTk(γ
FIRSTk(γ ) пусто при всех таких ωA
) пусто при всех таких ωA , что
, что  .
.
Доказательство. Необходимость. Допустим, что ω, A,  , β и γ удовлетворяют условиям теоремы, а FIRSTk(β
, β и γ удовлетворяют условиям теоремы, а FIRSTk(β )
)  FIRSTk(γ
FIRSTk(γ ) содержит x. Тогда по определению FIRST для некоторых y и z найдутся выводы
) содержит x. Тогда по определению FIRST для некоторых y и z найдутся выводы
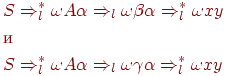
(Заметим, что здесь мы использовали тот факт, что N не содержит бесполезных нетерминалов, как это предполагается для всех рассматриваемых грамматик.) Если |x| < k; то y = z = e. Так как β  γ, то G не LL(k)-грамматика.
γ, то G не LL(k)-грамматика.
Достаточность. Допустим, что G не LL(k)-грамматика.
Тогда найдутся такие два вывода
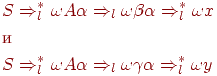
что цепочки x и y совпадают в первых k позициях, но β  γ. Поэтому A
γ. Поэтому A  β и A
β и A  γ - различные правила из P и каждое из множеств FIRSTk(β
γ - различные правила из P и каждое из множеств FIRSTk(β ) и FIRSTk(γ
) и FIRSTk(γ ) содержит цепочку FIRSTk(x), совпадающую с цепочкой FIRSTk(y).
) содержит цепочку FIRSTk(x), совпадающую с цепочкой FIRSTk(y).
Пример 4.8. Грамматика G, состоящая из двух правил S  aS | a, не будет LL(1)-грамматикой, так как
aS | a, не будет LL(1)-грамматикой, так как
FIRST1(aS) = FIRST1(a) = a.
Интуитивно это можно объяснить так: видя при разборе цепочки, начинающейся символом a, только этот первый символ, мы не знаем, какое из правил S  aS или S
aS или S  a надо применить к S. С другой стороны, G - это LL(2)-грамматика. В самом деле, в обозначениях только что представленной теоремы, если
a надо применить к S. С другой стороны, G - это LL(2)-грамматика. В самом деле, в обозначениях только что представленной теоремы, если  , то A = S и
, то A = S и  = e. Так как для S даны только два указанных правила, то β = aS и γ = a. Поскольку FIRST2(aS) = aa и FIRST2(a) = a, то по последней теореме G будет LL(2)-грамматикой.
= e. Так как для S даны только два указанных правила, то β = aS и γ = a. Поскольку FIRST2(aS) = aa и FIRST2(a) = a, то по последней теореме G будет LL(2)-грамматикой.
Удаление левой рекурсии
Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии. Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.
Непосредственную левую рекурсию, то есть рекурсию вида A A
A , можно удалить следующим способом. Сначала группируем A-правила:
, можно удалить следующим способом. Сначала группируем A-правила:
A  A
A 1 |A
1 |A 2| ... |A
2| ... |A m|β1|β2| ... |βn;
m|β1|β2| ... |βn;
где никакая из строк βi не начинается с A. Затем заменяем этот набор правил на
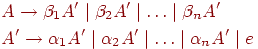
где A' - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии. С помощью этой процедуры удаляются все непосредственные левые рекурсии, но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.
Алгоритм 4.8. Удаление левой рекурсии.
Вход. КС-грамматика G без e-правил (вида A  e).
e).
Выход. КС-грамматика G' без левой рекурсии, эквивалентная G.
Метод. Выполнить шаги 1 и 2.
(1) Упорядочить нетерминалы грамматики G в произвольном порядке.
(2) Выполнить следующую процедуру:

После (i-1)-й итерации внешнего цикла на шаге 2 для любого правила вида Ak  As
As , где k < i, выполняется s > k. В результате на следующей итерации (по i) внутренний цикл (по j) последовательно увеличивает нижнюю границу по m в любом правиле Ai
, где k < i, выполняется s > k. В результате на следующей итерации (по i) внутренний цикл (по j) последовательно увеличивает нижнюю границу по m в любом правиле Ai  Am
Am , пока не будет m
, пока не будет m  i. Затем, после удаления непосредственной левой рекурсии для Ai-правил, m становится больше i.
i. Затем, после удаления непосредственной левой рекурсии для Ai-правил, m становится больше i.
Алгоритм 4.8 применим, если грамматика не имеет e- правил (правил вида A  e). Имеющиеся в грамматике e- правила могут быть удалены предварительно. Получающаяся грамматика без левой рекурсии может иметь e-правила.
e). Имеющиеся в грамматике e- правила могут быть удалены предварительно. Получающаяся грамматика без левой рекурсии может иметь e-правила.
Левая факторизация
Oсновная идея левой факторизации в том, что в том случае, когда неясно, какую из двух альтернатив надо использовать для развертки нетерминала A, нужно изменить A-правила так, чтобы отложить решение до тех пор, пока не будет достаточно информации для принятия правильного решения.
Если A 
 β1 |
β1 |  β2 - два A-правила и входная цепочка начинается с непустой строки, выводимой из
β2 - два A-правила и входная цепочка начинается с непустой строки, выводимой из  , мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув A
, мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув A 
 A'. Тогда после анализа того, что выводимо из
A'. Тогда после анализа того, что выводимо из  , можно развернуть по A'
, можно развернуть по A'  β1 или по A'
β1 или по A'  β2. Левофакторизованные правила принимают вид
β2. Левофакторизованные правила принимают вид
A
 A'
A'
A' β1|β2
β1|β2
Алгоритм 4.9. Левая факторизация грамматики.
Вход. КС-грамматика G.
Выход. Левофакторизованная КС-грамматика G', эквивалентная G.
Метод. Для каждого нетерминала A найти самый длинный префикс  , общий для двух или более его альтернатив. Если
, общий для двух или более его альтернатив. Если 
 e, то есть существует нетривиальный общий префикс, заменить все A-правила
e, то есть существует нетривиальный общий префикс, заменить все A-правила
A 
 β1|
β1| β2| ... |
β2| ... | βn|z,
βn|z,
где z обозначает все альтернативы, не начинающиеся с  , на
, на
A 
 A'|z
A'|z
A' β1|β2| ... |βn
β1|β2| ... |βn
где A' - новый нетерминал. Применять это преобразование, пока никакие две альтернативы не будут иметь общего префикса.
Пример 4.9. Рассмотрим вновь грамматику условных операторов из примера 4.6:
S  if E then S | if E then S else S | a
if E then S | if E then S else S | a
E  b
b
После левой факторизации грамматика принимает вид
S  if E then SS' | a
if E then SS' | a
S'  else S | e
else S | e
E  b
b
К сожалению, грамматика остается неоднозначной, а значит, и не LL(1)-грамматикой.
Рекурсивный спуск
Выше был рассмотрен один из вариантов таблично-управ- ляемого предсказывающего анализа, когда магазин явно использовался в процессе работы анализатора. Возможен иной вариант предсказывающего анализа, в котором каждому нетерминалу сопоставляется процедура (вообще говоря, рекурсивная), и магазин образуется неявно при вызовах таких процедур. Процедуры рекурсивного спуска могут быть записаны, как показано ниже.
В процедуре A для случая, когда имеется правило A  ui, такое, что
ui, такое, что  (напомним, что не может быть больше одного правила, из которого выводится e), приведены два варианта - 1.1 и 1.2. В варианте 1.1 делается проверка, принадлежит ли следующий входной символ FOLLOW(A): Если нет - выдается ошибка. В варианте 1.2 этого не делается, так что анализ ошибки откладывается на процедуру, вызвавшую A.
(напомним, что не может быть больше одного правила, из которого выводится e), приведены два варианта - 1.1 и 1.2. В варианте 1.1 делается проверка, принадлежит ли следующий входной символ FOLLOW(A): Если нет - выдается ошибка. В варианте 1.2 этого не делается, так что анализ ошибки откладывается на процедуру, вызвавшую A.

Восстановление процесса анализа после синтаксических ошибок
В приведенных программах рекурсивного спуска была использована процедура реакции на синтаксические ошибки error(). В простейшем случае эта процедура выдает диагностику и завершает работу анализатора. Но можно попытаться некоторым разумным образом продолжить работу. Для разбора сверху вниз можно предложить следующий простой алгоритм.
Если в момент обнаружения ошибки на верхушке магазина оказался нетерминальный символ A и для него нет правила, соответствующего входному символу, то сканируем вход до тех пор, пока не встретим символ либо из FIRST(A), либо из FOLLOW(A). В первом случае разворачиваем A по соответствующему правилу, во втором - удаляем A из магазина.
Если на верхушке магазина терминальный символ, то можно удалить все терминальные символы с верхушки магазина вплоть до первого (сверху) нетерминального символа и продолжать так, как это было описано выше.
Разбор снизу-вверх типа сдвиг- свертка
Основа
В процессе разбора снизу-вверх типа сдвиг-свертка строится дерево разбора входной цепочки, начиная с листьев (снизу) к корню (вверх). Этот процесс можно рассматривать как "свертку" цепочки w к начальному символу грамматики. На каждом шаге свертки подцепочка, которую можно сопоставить правой части некоторого правила вывода, заменяется символом левой части этого правила вывода, и если на каждом шаге выбирается правильная подцепочка, то в обратном порядке прослеживается правосторонний вывод (рис. 4.5) Здесь ко входной цепочке, так же как и при анализе LL(1)-грамматик, приписан концевой маркер $.
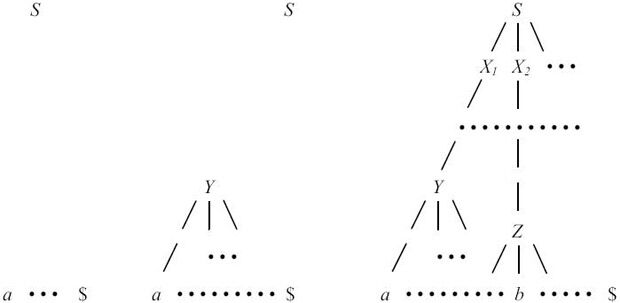
Рис. 4.5.
Основой цепочки называется подцепочка сентенциальной формы, которая может быть сопоставлена правой части некоторого правила вывода, свертка по которому к левой части правила соответствует одному шагу в обращении правостороннего вывода. Самая левая подцепочка, которая сопоставляется правой части некоторого правила вывода A  γ, не обязательно является основой, поскольку свертка по правилу A
γ, не обязательно является основой, поскольку свертка по правилу A  γ может дать цепочку, которая не может быть сведена к аксиоме.
γ может дать цепочку, которая не может быть сведена к аксиоме.
Формально, основа правой сентенциальной формы z - это правило вывода A  γ и позиция в z, в которой может быть найдена цепочка γ такие, что в результате замены γ на A получается предыдущая сентенциальная форма в правостороннем выводе z. Так, если
γ и позиция в z, в которой может быть найдена цепочка γ такие, что в результате замены γ на A получается предыдущая сентенциальная форма в правостороннем выводе z. Так, если  , то A
, то A  γ в позиции, следующей за
γ в позиции, следующей за  , это основа цепочки
, это основа цепочки  γβ. Подцепочка β справа от основы содержит только терминальные символы.
γβ. Подцепочка β справа от основы содержит только терминальные символы.
Вообще говоря, грамматика может быть неоднозначной, поэтому не единственным может быть правосторонний вывод  γβ и не единственной может быть основа. Если грамматика однозначна, то каждая правая сентенциальная форма грамматики имеет в точности одну основу. Замена основы в сентенциальной форме на нетерминал левой части называется отсечением основы. Обращение правостороннего вывода может быть получено с помощью повторного применения отсечения основы, начиная с исходной цепочки w. Если w - слово в рассматриваемой грамматике, то w =
γβ и не единственной может быть основа. Если грамматика однозначна, то каждая правая сентенциальная форма грамматики имеет в точности одну основу. Замена основы в сентенциальной форме на нетерминал левой части называется отсечением основы. Обращение правостороннего вывода может быть получено с помощью повторного применения отсечения основы, начиная с исходной цепочки w. Если w - слово в рассматриваемой грамматике, то w =  n, где
n, где  n - n-я правая сентенциальная форма еще неизвестного правого вывода
n - n-я правая сентенциальная форма еще неизвестного правого вывода  .
.
Чтобы восстановить этот вывод в обратном порядке, выделяем основу γn в  n и заменяем γn на левую часть некоторого правила вывода An
n и заменяем γn на левую часть некоторого правила вывода An  γn, получая (n - 1)-ю правую сентенциальную форму
γn, получая (n - 1)-ю правую сентенциальную форму  n-1. Затем повторяем этот процесс, то есть выделяем основу γn-1 в
n-1. Затем повторяем этот процесс, то есть выделяем основу γn-1 в  n-1 и сворачиваем эту основу, получая правую сентенциальную форму
n-1 и сворачиваем эту основу, получая правую сентенциальную форму  n-2. Если, повторяя этот процесс, мы получаем правую сентенциальную форму, состоящую только из начального символа S, то останавливаемся и сообщаем об успешном завершении разбора. Обращение последовательности правил, использованных в свертках, есть правый вывод входной строки.
n-2. Если, повторяя этот процесс, мы получаем правую сентенциальную форму, состоящую только из начального символа S, то останавливаемся и сообщаем об успешном завершении разбора. Обращение последовательности правил, использованных в свертках, есть правый вывод входной строки.
Таким образом, главная задача анализатора типа сдвиг- свертка - это выделение и отсечение основы.
LR(1)-анализаторы
В названии LR(1) символ L указывает на то, что входная цепочка читается слева-направо, R - на то, что строится правый вывод, наконец, 1 указывает на то, что анализатор видит один символ непрочитанной части входной цепочки.
LR(1)-анализ привлекателен по нескольким причинам:
- LR(1)-анализ - наиболее мощный метод анализа без возвратов типа сдвиг-свертка;
- LR(1)-анализ может быть реализован довольно эффективно;
- LR(1)-анализаторы могут быть построены для практически всех конструкций языков программирования;
- класс грамматик, которые могут быть проанализированы LR(1)-методом, строго включает класс грамматик, которые могут быть проанализированы предсказывающими анализаторами (сверху-вниз типа LL(1)).
Схематически структура LR(1)-анализатора изображена на рис. 4.4. Анализатор состоит из входной ленты, выходной ленты, магазина, управляющей программы и таблицы анализа (LR(1)-таблицы), которая имеет две части - функцию действий (Action) и функцию переходов (Goto). Управляющая программа одна и та же для всех LR(1)-анализаторов, разные анализаторы отличаются только таблицами анализа.
Анализатор читает символы на входной ленте по одному за шаг. В процессе анализа используется магазин, в котором хранятся строки вида S0X1S1X2S2 ... XmSm (Sm - верхушка магазина). Каждый Xi - символ грамматики (терминальный или нетерминальный), а Si - символ состояния.
Заметим, что символы грамматики (либо символы состояний) не обязательно должны размещаться в магазине. Однако, их использование облегчает понимание поведения LR-анализатора.
Элемент функции действий Action[Sm; ai] для символа состояния Sm и входа  , может иметь одно из четырех значений:
, может иметь одно из четырех значений:
- shift S (сдвиг), где S - символ состояния,
- reduce A
![]() γ (свертка по правилу грамматики A
γ (свертка по правилу грамматики A ![]() γ),
γ), - accept (допуск),
- error (ошибка).
Элемент функции переходов Goto[Sm; A] для символа состояния Smи входа  , может иметь одно из двух значений:
, может иметь одно из двух значений:
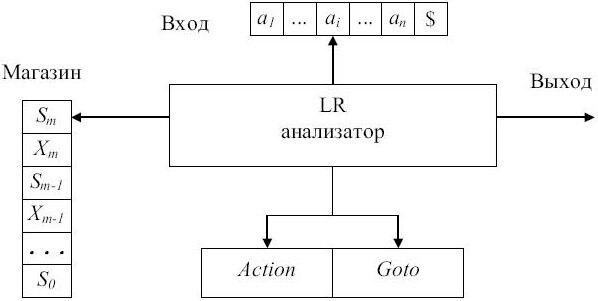
Рис. 4.6.
- S, где S - символ состояния,
- error (ошибка).
Конфигурацией LR(1)-анализатора называется пара, первая компонента которой - содержимое магазина, а вторая - непросмотренный вход:
(S0X1S1X2S2 ... XmSm, aiai+1 ... an$)
Эта конфигурация соответствует правой сентенциальной форме
X1X2 ... Xmaiai+1 ... an
Префиксы правых сентенциальных форм, которые могут появиться в магазине анализатора, называются активными префиксами. Основа сентенциальной формы всегда располагается на верхушке магазина. Таким образом, активный префикс - это такой префикс правой сентенциальной формы, который не переходит правую границу основы этой формы.
Когда анализатор начинает работу, в магазине находится только символ начального состояния S0, на входной ленте - анализируемая цепочка с маркером конца.
Каждый очередной шаг анализатора определяется текущим входным символом ai и символом состояния на верхушке магазина Sm следующим ниже образом.
Пусть LR(1)-анализатор находится в конфигурации
(S0X1S1X2S2 ... XmSm, aiai+1 ... an$)
Анализатор может проделать один из следующих шагов:
- Если Action[Sm, ai] = shift S, то анализатор выполняет сдвиг, переходя в конфигурацию
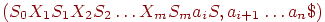
То есть, в магазин помещаются входной символ ai и символ состояния S, определяемый Action[Sm, ai]. Текущим входным символом становится ai+1.
- Если Action[Sm, ai] = reduce A
![]() γ, то анализатор выполняет свертку, переходя в конфигурацию
γ, то анализатор выполняет свертку, переходя в конфигурацию
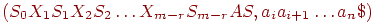
где S = Goto[Sm-r; A] и r - длина γ, правой части правила вывода. Анализатор сначала удаляет из магазина 2r символов (r символов состояния и r символов грамматики), так что на верхушке оказывается состояние Sm-r. Затем анализатор помещает в магазин A - левую часть правила вывода, и S - символ состояния, определяемый Goto[Sm-r, A]. На шаге свертки текущий входной символ не меняется. Для LR(1)- анализаторов последовательность символов грамматики Xm-r+1 ... Xm, удаляемых из магазина , всегда соответствует γ - правой части правила вывода, по которому делается свертка. После осуществления шага свертки генерируется выход LR(1)-анализатора, то есть исполняются семантические действия, связанные с правилом, по которому делается свертка, например, печатаются номера правил, по которым делается свертка. Заметим, что функция Goto таблицы анализа, построенная по грамматике G, фактически представляет собой функцию переходов детерминированного конечного автомата, распознающего активные префиксы G.
- Если Action[Sm, ai] = accept, то разбор успешно завершен.
- Если Action[Sm, ai] = error, то анализатор обнаружил ошибку, и выполняются действия по диагностике и восстановлению.
Пример 4.10. Рассмотрим грамматику арифметических выражений G = ({E, T, F}, {id, +, *}, P, E) с правилами:
- E
![]() E + T
E + T - E
![]() T
T - T
![]() T * F
T * F - T
![]() F
F - F
![]() id
id
На рис. 4.7 изображены функции Action и Goto, образующие LR(1)-таблицу для этой грамматики. Элемент Si функции Action означает сдвиг и помещение в магазин состояния с номером i, Rj - свертку по правилу номер j, acc - допуск, пустая клетка - ошибку. Для функции Goto символ i означает помещение в магазин состояния с номером i, пустая клетка - ошибку.
На входе id + id * id последовательность состояний магазина и входной ленты показаны на рис. 4.8. Например, в первой строке LR-анализатор находится в нулевом состоянии и "видит" первый входной символ id. Действие S6 в нулевой строке и столбце id в поле Action (рис. 4.7) означает сдвиг и помещение символа состояния 6 на верхушку магазина. Это и изображено во второй строке: первый символ id и символ состояния 6 помещаются в магазин, а id удаляется со входной ленты.
Текущим входным символом становится +, и действием в состоянии 6 на вход + является свертка по F  id. Из магазина удаляются два символа (один символ состояния и один символ грамматики). Затем анализируется нулевое состояние. Поскольку Goto в нулевом состоянии по символу F - это 3, F и 3 помещаются в магазин. Теперь имеем конфигурацию, соответствующую третьей строке. Остальные шаги определяются аналогично.
id. Из магазина удаляются два символа (один символ состояния и один символ грамматики). Затем анализируется нулевое состояние. Поскольку Goto в нулевом состоянии по символу F - это 3, F и 3 помещаются в магазин. Теперь имеем конфигурацию, соответствующую третьей строке. Остальные шаги определяются аналогично.
Конструирование LR(1)-таблицы
Рассмотрим алгоритм конструирования таблицы, управляющей LR(1) - анализатором.
Пусть G = (N, T, P, S) - КС-грамматика. Пополненной грамматикой для данной грамматики G называется КС- Состояния Action Goto
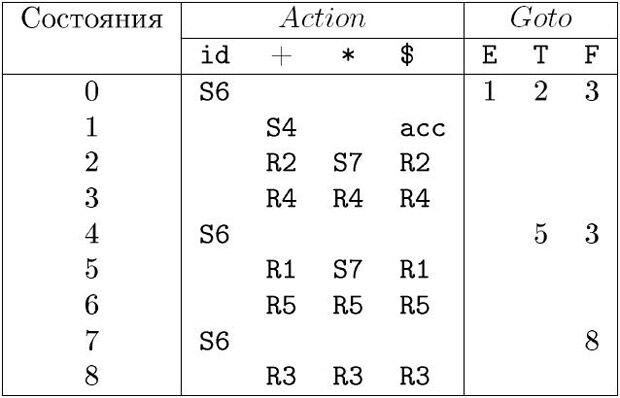
Рис. 4.7.
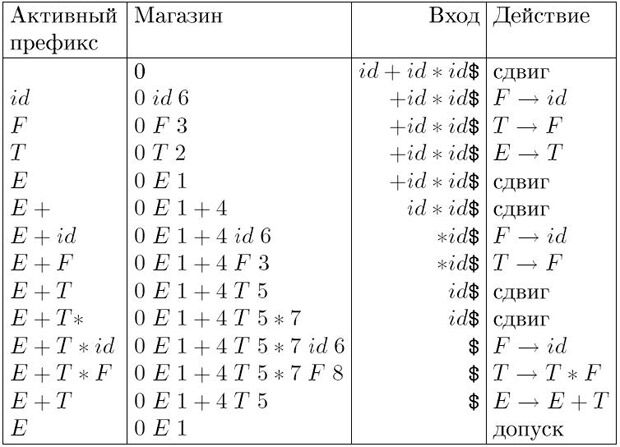
Рис. 4.8.
грамматика
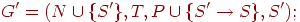
то есть эквивалентная грамматика, в которой введен новый начальный символ S' и новое правило вывода S'  S.
S.
Это дополнительное правило вводится для того, чтобы определить, когда анализатор должен остановить разбор и зафиксировать допуск входа. Таким образом, допуск имеет место тогда и только тогда, когда анализатор готов осуществить свертку по правилу S'  S.
S.
LR(1)-ситуацией называется пара [A 
 .β, a], где A
.β, a], где A 
 β - правило грамматики, a - терминал или правый концевой маркер $. Вторая компонента ситуации называется аванцепочкой.
β - правило грамматики, a - терминал или правый концевой маркер $. Вторая компонента ситуации называется аванцепочкой.
Будем говорить, что LR(1)-ситуация [A 
 .β, a] допустима для активного префикса +, если существует вывод
.β, a] допустима для активного префикса +, если существует вывод  , где + = γ
, где + = γ и либо a - первый символ w, либо w = e и a = $.
и либо a - первый символ w, либо w = e и a = $.
Будем говорить, что ситуация допустима, если она допустима для какого-либо активного префикса.
Пример 4.11. Дана грамматика G = ({S, B}, {a, b}, P, S) с правилами
S  BB
BB
B  aB | b
aB | b
Существует правосторонний вывод  . Легко видеть, что ситуация [B
. Легко видеть, что ситуация [B  a.B, a] допустима для активного префикса + = aaa, если в определении выше положить γ = aa, A = B, w = ab,
a.B, a] допустима для активного префикса + = aaa, если в определении выше положить γ = aa, A = B, w = ab,  = a, β = B. Существует также правосторонний вывод
= a, β = B. Существует также правосторонний вывод  . Поэтому для активного префикса Baa допустима ситуация [B
. Поэтому для активного префикса Baa допустима ситуация [B  a.B, $].
a.B, $].
Центральная идея метода заключается в том, что по грамматике строится детерминированный конечный автомат, распознающий активные префиксы. Для этого ситуации группируются во множества, которые и образуют состояния автомата. Ситуации можно рассматривать как состояния недетерминированного конечного автомата, распознающего активные префиксы, а их группировка на самом деле есть процесс построения детерминированного конечного автомата из недетерминированного.
Анализатор, работающий слева-направо по типу сдвиг- свертка, должен уметь распознавать основы на верхушке магазина. Состояние автомата после прочтения содержимого магазина и текущий входной символ определяют очередное действие автомата. Функцией переходов этого конечного автомата является функция переходов LR-анализатора.
Чтобы не просматривать магазин на каждом шаге анализа, на верхушке магазина всегда хранится то состояние, в котором должен оказаться этот конечный автомат после того, как он прочитал символы грамматики в магазине от дна к верхушке. Рассмотрим ситуацию вида [A 
 .Bβ, a] из множества ситуаций, допустимых для некоторого активного префикса z. Тогда существует правосторонний вывод
.Bβ, a] из множества ситуаций, допустимых для некоторого активного префикса z. Тогда существует правосторонний вывод  , где z = y
, где z = y . Предположим, что из βax выводится терминальная строка bw. Тогда для некоторого правила вывода вида B
. Предположим, что из βax выводится терминальная строка bw. Тогда для некоторого правила вывода вида B  q имеется вывод
q имеется вывод  . Таким образом [B
. Таким образом [B  .q, b] также допустима для z и ситуация [A
.q, b] также допустима для z и ситуация [A 
 B.β, a] допустима для активного префикса zB. Здесь либо b может быть первым терминалом, выводимым из β, либо из β выводится e в выводе
B.β, a] допустима для активного префикса zB. Здесь либо b может быть первым терминалом, выводимым из β, либо из β выводится e в выводе  и тогда b равно a. То есть b принадлежит FIRST(β ax). Построение всех таких ситуаций для данного множества ситуаций, то есть его замыкание, делает приведенная ниже функция closure.
и тогда b равно a. То есть b принадлежит FIRST(β ax). Построение всех таких ситуаций для данного множества ситуаций, то есть его замыкание, делает приведенная ниже функция closure.
Система множеств допустимых LR(1)-ситуаций для всевозможных активных префиксов пополненной грамматики называется канонической системой множеств допустимых LR(1)-ситуаций. Алгоритм построения канонической системы множеств приведен ниже.
Алгоритм 4.10. Конструирование канонической системы множеств допустимых LR(1)-ситуаций.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Каноническая система C множеств допустимых LR(1)-ситуаций для грамматики G.
Метод. Выполнить для пополненной грамматики G' процедуру items, которая использует функции closure и goto.
function closure(I){ /* I - множество ситуаций */
do{
for (каждой ситуации [A 
 .Bβ, a] из I,
.Bβ, a] из I,
каждого правила вывода B  γ из G',
γ из G',
каждого терминала b из FIRST(βa),
такого, что [B  .γ, b] нет в I)
.γ, b] нет в I)
добавить [B  .γ, b] к I;
.γ, b] к I;
}
while (к I можно добавить новую ситуацию);
return I;
}
function goto(I,X){ /* I - множество ситуаций;
X - символ грамматики */
Пусть J = {[A 
 X.β; a] | [A
X.β; a] | [A 
 .Xβ, a] in I};
.Xβ, a] in I};
return closure(J);
}
procedure items(G'){ /* G' - пополненная
грамматика */
I' = closure({[S'  .S, $]});
.S, $]});
C = {I0};
do{
for (каждого множества ситуаций I из
системы C, каждого символа грамматики X
такого, что goto(I, X) не пусто
и не принадлежит C)
добавить goto(I, X) к системе C;
}
while (к C можно добавить новое множество
ситуаций);
Если I - множество ситуаций, допустимых для некоторого активного префикса +, то goto(I, X) - множество ситуаций, допустимых для активного префикса +X.
Работа алгоритма построения системы C множеств допустимых LR(1)-ситуаций начинается с того, что в C помещается начальное множество ситуаций I0 = closure({[S'  .S, $]}). Затем с помощью функции goto вычисляются новые множества ситуаций и включаются в C.
.S, $]}). Затем с помощью функции goto вычисляются новые множества ситуаций и включаются в C.
По-существу, goto(I, X) - переход конечного автомата из состояния I по символу X.
Рассмотрим теперь, как по системе множеств LR(1)-ситу- аций строится LR(1)-таблица, то есть функции действий и переходов LR(1)-анализатора.
Алгоритм 4.11. Построение LR(1)-таблицы.
Вход. Каноническая система C = {I0, I1, ... , In} множеств допустимых LR(1)-ситуаций для грамматики G.
Выход. Функции Action и Goto, составляющие LR(1)- таблицу для грамматики G.
Метод. Для каждого состояния i функции Action[i, a] и Goto[i, X] строятся по множеству ситуаций Ii:
- Значения функции действия (Action) для состояния i определяются следующим образом:
- если
![[A rightarrow alpha .a beta , b] in I_i]() (a - терминал) и goto(Ii, a)= Ij , то полагаем Action[i, a] = shift j;
(a - терминал) и goto(Ii, a)= Ij , то полагаем Action[i, a] = shift j; - если
![[A rightarrow alpha; ., a] in I_i]() , причем A
, причем A ![]() S', то полагаем Action[i, a] = reduce A
S', то полагаем Action[i, a] = reduce A ![]()
![]() ;
; - если
![[S' rightarrow S., $] in I_i]() , то полагаем Action[i, $] = accept.
, то полагаем Action[i, $] = accept. - Значения функции переходов для состояния i определяются следующим образом: если goto(Ii, A) = Ij , то Goto[i, A] = j (здесь A - нетерминал).
- Все входы в Action и Goto, не определенные шагами 2 и 3, полагаем равными error.
- Начальное состояние анализатора строится из множества, содержащего ситуацию [S'
![]() .S, $].
.S, $].
Таблица на основе функций Action и Goto, полученных в результате работы алгоритма 4.11., называется канонической LR(1)-таблицей. Работающий с ней LR(1)-анализатор, называется каноническим LR(1)-анализатором.
Пример 4.12. Рассмотрим следующую грамматику, являющуюся пополненной для грамматики из примера 4.8.:
(0) E'  E
E
(1) E  E + T
E + T
(2) E  T
T
(3) T  T * F
T * F
(4) T  F
F
(5) F  id.
id.
Множества ситуаций и переходы по goto для этой грамматики приведены на рис. 4.9. LR(1)-таблица для этой грамматики приведена на рис. 4.7.
Проследим последовательность создания этих множеств более подробно.
- Вычисляем I0 = closure({[E'
![]() .E, $]}).
.E, $]}). - Ситуация [E'
![]() .E, $] попадает в него по умолчанию как исходная.
.E, $] попадает в него по умолчанию как исходная. - Если обратиться к обозначениям функции closure, то для нее
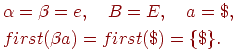
Значит, для терминала $ добавляем ситуации на основе правил со знаком E в левой части правила. Это правила
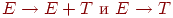
и соответствующие им ситуации
![begin{align*} & [E rightarrow. E + T, $] text{ и } [E rightarrow . T, $] end{align*}](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/490-4-sintaksicheskiy-analiz.png)
- Просматриваем получившиеся ситуации. Для ситуации [E
![]() .E + T, $] β = +, поэтому first(βa) = first(+$) = {+}. На основе этого добавляем к I0 [E
.E + T, $] β = +, поэтому first(βa) = first(+$) = {+}. На основе этого добавляем к I0 [E ![]() E + .T, +] и [E
E + .T, +] и [E ![]() .T, +].
.T, +]. - Для ситуации [E
![]() .T, $] β = e, first(βa) = {$}. Поэтому добавляем к I0 [T
.T, $] β = e, first(βa) = {$}. Поэтому добавляем к I0 [T ![]() . T * F, $] и [T
. T * F, $] и [T ![]() .F, $].
.F, $]. - Подобно этому для ситуации [E
![]() .T, +] β = e, first(βa) = {+}. Поэтому добавляем к I0 [T
.T, +] β = e, first(βa) = {+}. Поэтому добавляем к I0 [T ![]() .T * F, +] и [T
.T * F, +] и [T ![]() .F, +].
.F, +]. - Из ситуации [T
![]() . T * F, +] β = *, first(βa) = {*}: Поэтому добавляем к I0
. T * F, +] β = *, first(βa) = {*}: Поэтому добавляем к I0
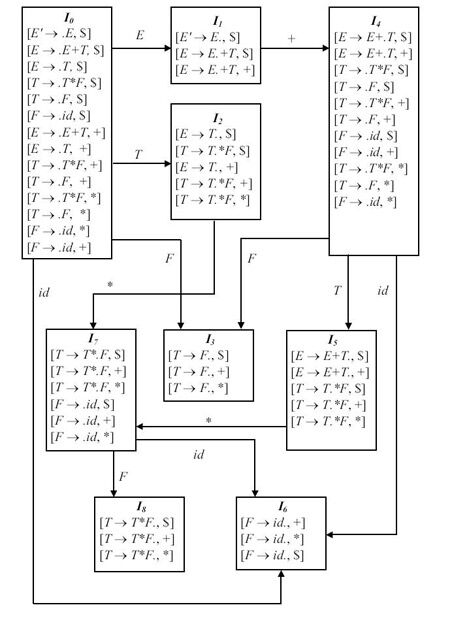
увеличить изображение
Рис. 4.9.
[T  .T * F, *] и [T
.T * F, *] и [T  .F, *]
.F, *]
- Далее из ситуации [T
![]() .F, *] получаем ситуацию [F
.F, *] получаем ситуацию [F ![]() . id, *]. из ситуации [T
. id, *]. из ситуации [T ![]() . F, $] - ситуацию [F
. F, $] - ситуацию [F ![]() . id, $], а из ситуации [T
. id, $], а из ситуации [T ![]() . F, +] - [F
. F, +] - [F ![]() . id, *].
. id, *].
Таким образом, все 14 искомых ситуаций I0 получены.
Возвращаемся в головную функцию items, включаем I0 в множество C и исследуем непустые итоги применения функции goto(I0; X), где  .
.
Если посмотреть на вид правил в функции goto(I0; X), то видно, что X должен встретиться в правой части хотя бы одного правила. Для E0 таких правил у нас нет, поэтому значение функции goto(I0, E') пусто.
Возьмем goto(I0; E). E встречается после точки в правых частях двух ситуаций из I0, значит берем эти два правила и переносим в них точки на один символ вправо (пока есть куда - не уперлись в запятую), получаем:
[E'  E., $]
E., $]
и
[E  E. + T, $|+]
E. + T, $|+]
Вычислим от каждой из этих ситуаций функцию closure. Но, поскольку справа от точки здесь либо пустая цепочка, либо терминал, то никаких новых ситуаций не возникает. Дальше отслеживаем, может ли куда-то сдвинуться точка дальше на право и по какому символу. Если может, строим соответствующее множество (рис. 4.9). И т.д.
LR(1)-грамматики
Если для КС-грамматики G функция Action, полученная в результате работы алгоритма 4.11., не содержит неоднозначно определенных входов, то грамматика называется LR(1)- грамматикой.
Язык L называется LR(1)-языком, если он может быть порожден некоторой LR(1)-грамматикой.
Иногда используется другое определение LR(1)-грамматики. Грамматика называется LR(1), если из условий
![S' Rightarrow^*_r uAw Rightarrow_r uvw]()
![S' Rightarrow^*_r zBx Rightarrow_r uvy]()
- FIRST(w)=FIRST(y)
следует, что uAy = zBx (то есть u = z, A = B и x = y).
Согласно этому определению, если uvw и uvy - правовыводимые цепочки пополненной грамматики, у которых FIRST(w) = FIRST(y) и A  β - последнее правило, использованное в правом выводе цепочки uvw, то правило A
β - последнее правило, использованное в правом выводе цепочки uvw, то правило A  β должно применяться и в правом разборе при свертке uvy к uAy. Так как A дает β независимо от w, то LR(1)-условие означает, что в FIRST(w) содержится информация, достаточная для определения того, что uv за один шаг выводится из uA. Поэтому никогда не может возникнуть сомнений относительно того, как свернуть очередную правовыводимую цепочку пополненной грамматики.
β должно применяться и в правом разборе при свертке uvy к uAy. Так как A дает β независимо от w, то LR(1)-условие означает, что в FIRST(w) содержится информация, достаточная для определения того, что uv за один шаг выводится из uA. Поэтому никогда не может возникнуть сомнений относительно того, как свернуть очередную правовыводимую цепочку пополненной грамматики.
Можно доказать, что эти два определения эквивалентны. Дадим теперь определение LR(k)-грамматики.
Определение. Пусть G = (N, Σ, P, S) - КС-грамматика и G' = (N', Σ, P', S') - полученная из нее пополненная грамматика. Будем называть G LR(k)-грамматикой для k  0, если из условий
0, если из условий
(1) 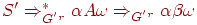
(2)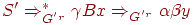
(3)FIRSTk(w) = FIRSTk(y)
следует, что  Ay = γBx (т.е.
Ay = γBx (т.е.  = γ, A = B и x = y):
= γ, A = B и x = y):
Грамматика G называется LR-грамматикой, если она LR(k)-грамматика для некоторого k  0:
0:
Интуитивно это определение говорит о том, что если  βw и
βw и  βy - правовыводимые цепочки пополненной грамматики, у которых FIRSTk(w) = FIRSTk(y), и A
βy - правовыводимые цепочки пополненной грамматики, у которых FIRSTk(w) = FIRSTk(y), и A  β - последнее правило, использованное в правом выводе цепочки
β - последнее правило, использованное в правом выводе цепочки  βw, то правило A
βw, то правило A  β должно использоваться также в правом разборе при свертке
β должно использоваться также в правом разборе при свертке  βy к
βy к  Ay. Так как A даeт β независимо от w, то LR(k)-условие говорит о том, что в FIRSTk(w) содержится информация, достаточная для определения того, что
Ay. Так как A даeт β независимо от w, то LR(k)-условие говорит о том, что в FIRSTk(w) содержится информация, достаточная для определения того, что  β за один шаг выводится из
β за один шаг выводится из  A. Поэтому никогда не может возникнуть сомнений относительно того, как свернуть очередную правовыводимую цепочку пополненной грамматики. Кроме того, работая с LR(k)-грамматикой, мы всегда знаем, допустить ли данную входную цепочку или продолжать разбор.
A. Поэтому никогда не может возникнуть сомнений относительно того, как свернуть очередную правовыводимую цепочку пополненной грамматики. Кроме того, работая с LR(k)-грамматикой, мы всегда знаем, допустить ли данную входную цепочку или продолжать разбор.
Пример 4.13. Рассмотрим грамматику G с правилами
S  Sa|a
Sa|a
Согласно определению, G не LR(0)-грамматика, так как из трeх условий
(1)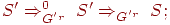
(2)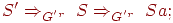
(3)FIRST0(e) = FIRST0(a) = e
не следует, что S'a = S: Применяя определение к этой ситуации, имеем  = e; β = S; ω = e; γ = e; A = S', B = S; x = e и y = a. Проблема здесь заключается в том, что нельзя установить, является ли S основой правовыводимой цепочки Sa, не видя символа, стоящего после S (т.е. наблюдая "нулевое" количество символов). В соответствии с интуицией G не должна быть LR(0)- грамматикой и она не будет ею, если пользоваться первым определением. Это определение мы и будем использовать далее.
= e; β = S; ω = e; γ = e; A = S', B = S; x = e и y = a. Проблема здесь заключается в том, что нельзя установить, является ли S основой правовыводимой цепочки Sa, не видя символа, стоящего после S (т.е. наблюдая "нулевое" количество символов). В соответствии с интуицией G не должна быть LR(0)- грамматикой и она не будет ею, если пользоваться первым определением. Это определение мы и будем использовать далее.
Пример 4.14. Пусть G - леволинейная грамматика с правилами
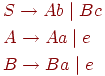
Заметим, что G не является LR(k)-грамматикой ни для какого k.
Допустим, что G - LR(k)-грамматика. Рассмотрим два правых вывода в пополненной грамматике G':
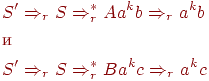
Эти два вывода удовлетворяют условию из определения LR(k)- грамматики при  = e, β = e, ω = akb, γ = e и y = akc: Но так как заключение неверно, т.е. A
= e, β = e, ω = akb, γ = e и y = akc: Но так как заключение неверно, т.е. A  B, то G - не LR(k)-грамматика. Более того, так как LR(k)-условие нарушается для всех k, то G - не LR-грамматика.
B, то G - не LR(k)-грамматика. Более того, так как LR(k)-условие нарушается для всех k, то G - не LR-грамматика.
Если грамматика не является LR(1), то анализатор типа сдвиг-свертка при анализе некоторой цепочки может достигнуть конфигурации, в которой он, зная содержимое магазина и следующий входной символ, не может решить, делать ли сдвиг или свертку (конфликт сдвиг/свертка), или не может решить, какую из нескольких сверток применить (конфликт свертка/свертка).
В частности, неоднозначная грамматика не может быть LR(1). Для доказательства рассмотрим два различных правых вывода
(1) 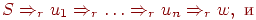
(2) 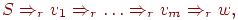
Нетрудно заметить, что LR(1) - условие (согласно второму определению LR(1)-грамматики) нарушается для наименьшего из чисел i, для которых un-i  vm-i.
vm-i.
Пример 4.15. Рассмотрим ещe раз грамматику условных операторов:
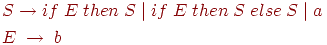
Если анализатор типа сдвиг-свертка находится в конфигурации, такой, что необработанная часть входной цепочки имеет вид else ... $, а в магазине находится ... if E then S, то нельзя определить, является ли if E then S основой, вне зависимости от того, что лежит в магазине ниже. Это конфликт сдвиг/свертка. В зависимости от того, что следует на входе за else, правильной может быть свертка по S  if E then S или сдвиг else, а затем разбор другого S и завершение основы if E then S else S. Таким образом нельзя сказать, нужно ли в этом случае делать сдвиг или свертку, так что грамматика не является LR(1).
if E then S или сдвиг else, а затем разбор другого S и завершение основы if E then S else S. Таким образом нельзя сказать, нужно ли в этом случае делать сдвиг или свертку, так что грамматика не является LR(1).
Эта грамматика может быть преобразована к LR(1)-виду следующим образом:
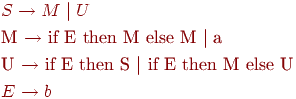
Основная разница между LL(1)- и LR(1)- грамматиками заключается в следующем. Чтобы грамматика была LR(1)- грамматикой, необходимо распознавать вхождение правой части правила вывода, просмотрев все, что выведено из этой правой части и текущий символ входной цепочки. Это требование существенно менее строгое, чем требование для LL(1)-грамматики, когда необходимо определить применимое правило, видя только первый символ, выводимый из его правой части. Таким образом, класс LL(1)-грамматик есть собственный подкласс класса LR(1)-грамматик.
Справедливы также следующие утверждения [2].
Теорема 4.7. Каждый LR(1)-язык является детерминированным КС-языком.
Теорема 4.8. Если L - детерминированный КС-язык, то существует LR(1)-грамматика, порождающая L.
Теорема 4.9. Для любой LR(k)-грамматики для k > 1 существует эквивалентная ей LR(k Gamma 1)-грамматика.
Доказано, что проблема определения, порождает ли грамматика LR-язык, является алгоритмически неразрешимой.
Восстановление процесса анализа после синтаксических ошибок
Одним из простейших методов восстановления после ошибки при LR(1)-анализе является следующий. При синтаксической ошибке просматриваем магазин от верхушки, пока не найдем состояние s с переходом на выделенный нетерминал A. Затем сканируются входные символы, пока не будет найден такой, который допустим после A. В этом случае на верхушку магазина помещается состояние Goto[s, A] и разбор продолжается. Для нетерминала A может иметься несколько таких вариантов. Обычно A - это нетерминал, представляющий одну из основных конструкций языка, например оператор.
В лекции "2 - Клеточная оболочка" также много полезной информации.
При более детальной проработке реакции на ошибки можно в каждой пустой клетке анализатора поставить обращение к своей подпрограмме. Такая подпрограмма может вставлять или удалять входные символы или символы магазина, менять порядок входных символов.
Варианты LR-анализаторов
Часто построенные таблицы для LR(1)-анализатора оказываются довольно большими. Поэтому при практической реализации используются различные методы их сжатия. С другой стороны, часто оказывается, что при построении для языка синтаксического анализатора типа "сдвиг-свертка" достаточно более простых методов. Некоторые из этих методов базируются на основе LR(1)-анализаторов.
Одним из способов такого упрощения является LR(0)- анализ - частный случая LR-анализа, когда ни при построении таблиц, ни при анализе не учитывается аванцепочка.
Еще одним вариантом LR-анализа являются так называемые SLR(1)-анализаторы (Simple LR(1)). Они строятся следующим образом. Пусть C = {I0, I1, ... , In} - набор множеств допустимых LR(0)-ситуаций. Состояния анализатора соответствуют Ii. Функции действий и переходов анализатора определяются следующим образом.
- Если
![[A rightarrow u.av] in I_i text{ и } goto(I_i, a) = I_j]() , то определим Action[i, a] = shift j.
, то определим Action[i, a] = shift j. - Если
![[A rightarrow u.] in I_i]() , то, для всех
, то, для всех ![a in FOLLOW(A)]() , A
, A ![]() S', определим Action[i, a] = reduce A
S', определим Action[i, a] = reduce A ![]() u
u - Если
![[S' rightarrow S.] in I_i]() , то определим Action[i, $] = accept.
, то определим Action[i, $] = accept. - Если goto(Ii, A) = Ij , где
![A in N]() , то определим Goto[i, A] = j.
, то определим Goto[i, A] = j. - Остальные входы для функций Action и Goto определим как error.
- Начальное состояние соответствует множеству ситуаций, содержащему ситуацию [S'
![]() .S]
.S]
Распространенным вариантом LR(1)-анализа является также LALR(1)-анализ. Он основан на объединении (слиянии) некоторых таблиц. Назовем ядром множества LR(1)-ситуаций множество их первых компонент (то есть во множестве ситуаций не учитываются аванцепочки). Объединим все множества ситуаций с одинаковыми ядрами, а в качестве аванцепочек возьмем объединение аванцепочек. Функции Action и Goto строятся очевидным образом. Если функция Action таким образом построенного анализатора не имеет конфликтов, то он называется LALR(1)-анализатором (LookAhead LR(1)).Если грамматика является LR(1), то в таблицах LALR(1) анализатора могут появиться конфликты типы свертка-свертка (если одно из объединяемых состояний имело ситуации [A 
 , a] и [B
, a] и [B  β, b], а другое [A
β, b], а другое [A 
 , b] и [B
, b] и [B  β a], то в LALR(1) появятся ситуации [A
β a], то в LALR(1) появятся ситуации [A 
 , {a, b}] и [B
, {a, b}] и [B  β, {b, a}]). Конфликты типа сдвиг-свертка появиться не могут, поскольку аванцепочка для сдвига во внимание не принимается.
β, {b, a}]). Конфликты типа сдвиг-свертка появиться не могут, поскольку аванцепочка для сдвига во внимание не принимается.

 , то
, то  для всех
для всех  и
и  (моделирование М),
(моделирование М), (начало работы),
(начало работы), множество D'(q, e, Z) содержит (qe, e) (переход в состояние сокращения магазина без продвижения),
множество D'(q, e, Z) содержит (qe, e) (переход в состояние сокращения магазина без продвижения), определим
определим  - работа в "режиме M" ,
- работа в "режиме M" , - переход в заключительное состояние.
- переход в заключительное состояние. , то
, то  ,
,![S rightarrow [q_0Z_0q] in P](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/67-4-sintaksicheskiy-analiz.png) для всех
для всех ![(r, e) in D(q, a, Z), ; text{то} ; [qZr] rightarrow a in P, a in T cup {e}](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/69-4-sintaksicheskiy-analiz.png) ,
, , то
, то![[A rightarrow alpha .a beta , b] in I_i](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/473-4-sintaksicheskiy-analiz.png) (a - терминал) и goto(Ii, a)= Ij , то полагаем Action[i, a] = shift j;
(a - терминал) и goto(Ii, a)= Ij , то полагаем Action[i, a] = shift j;![[A rightarrow alpha; ., a] in I_i](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/474-4-sintaksicheskiy-analiz.png) , причем A
, причем A ![[S' rightarrow S., $] in I_i](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/478-4-sintaksicheskiy-analiz.png) , то полагаем Action[i, $] = accept.
, то полагаем Action[i, $] = accept.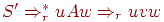
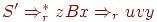
![[A rightarrow u.av] in I_i text{ и } goto(I_i, a) = I_j](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/546-4-sintaksicheskiy-analiz.png) , то определим Action[i, a] = shift j.
, то определим Action[i, a] = shift j.![[A rightarrow u.] in I_i](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/547-4-sintaksicheskiy-analiz.png) , то, для всех
, то, для всех  , A
, A ![[S' rightarrow S.] in I_i](https://s.studizba.com/z.php?f=/uploads/lectures/informatika-i-programmirovanie/kompilyatory/files/551-4-sintaksicheskiy-analiz.png) , то определим Action[i, $] = accept.
, то определим Action[i, $] = accept.
















