Лексический анализ
3. Лекция: Лексический анализ
В данной лекции приводится понятие лексического анализа. Рассмотрены основные задачи лексического анализа, приведены основные определения, такие как регулярное множество, конечный автомат, конфигурация, лексический анализатор. Также приведены примеры решения задач, связанных с лексическим анализом. 


Основная задача лексического анализа - разбить входной текст, состоящий из последовательности одиночных символов, на последовательность слов, или лексем, то есть выделить эти слова из непрерывной последовательности символов. Все символы входной последовательности с этой точки зрения разделяются на символы, принадлежащие каким-либо лексемам, и символы, разделяющие лексемы (разделители). В некоторых случаях между лексемами может и не быть разделителей. С другой стороны, в некоторых языках лексемы могут содержать незначащие символы (например, символ пробела в Фортране). В Си разделительное значение символов-разделителей может блокироваться ("" в конце строки внутри "...").
Обычно все лексемы делятся на классы. Примерами таких классов являются числа (целые, восьмеричные, шестнадцатиричные, действительные и т.д.), идентификаторы, строки. Отдельно выделяются ключевые слова и символы пунктуации (иногда их называют символы-ограничители). Как правило, ключевые слова - это некоторое конечное подмножество идентификаторов. В некоторых языках (например, ПЛ/1) смысл лексемы может зависеть от ее контекста и невозможно провести лексический анализ в отрыве от синтаксического.
Для осуществления двух дальнейших фаз анализа лексический анализатор выдает информацию двух типов: для синтаксического анализатора, работающего вслед за лексическим, существенна информация о последовательности классов лексем, ограничителей и ключевых слов, а для контекстного анализатора, работающего вслед за синтаксическим, существенна информация о конкретных значениях отдельных лексем (идентификаторов, чисел и т.д.).
Таким образом, общая схема работы лексического анализатора такова. Сначала выделяется отдельная лексема (при этом, возможно, используются символы- разделители). Ключевые слова распознаются явным выделением непосредственно из текста, либо сначала выделяется идентификатор, а затем делается проверка на принадлежность его множеству ключевых слов.
Если выделенная лексема является ограничителем, то этот ограничитель (точнее, некоторый его признак) выдается как результат лексического анализа. Если выделенная лексема является ключевым словом, то выдается признак соответствующего ключевого слова. Если выделенная лексема является идентификатором - выдается признак идентификатора, а сам идентификатор сохраняется отдельно. Наконец, если выделенная лексема принадлежит какому-либо из других классов лексем (например, лексема представляет собой число, строку и т.д.), то выдается признак соответствующего класса, а значение лексемы сохраняется отдельно.
Лексический анализатор может быть как самостоятельной фазой трансляции, так и подпрограммой, работающей по принципу "дай лексему". В первом случае (рис. 3.1, а) выходом анализатора является файл лексем, во втором - (рис. 3.1., б) лексема выдается при каждом обращении к анализатору (при этом, как правило, признак класса лексемы возвращается как результат функции "лексический анализатор", а значение лексемы передается через глобальную переменную). С точки зрения обработки значений лексем, анализатор может либо просто выдавать значение каждой лексемы, при этом построение таблиц объектов (идентификаторов, строк, чисел и т.д.) переносится на более поздние фазы, либо он может самостоятельно строить таблицы объектов. В этом случае в качестве значения лексемы выдается указатель на вход в соответствующую таблицу.
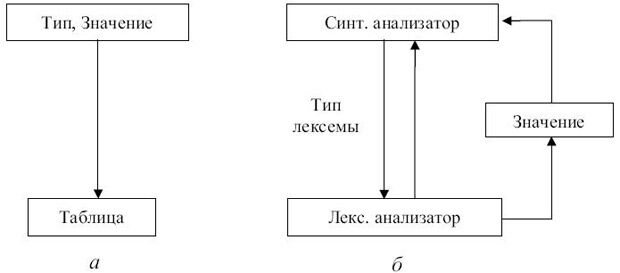
Рис. 3.1.
Рекомендуемые материалы
Работа лексического анализатора задается некоторым конечным автоматом. Однако, непосредственное описание конечного автомата неудобно с практической точки зрения. Поэтому для задания лексического анализатора, как правило, используется либо регулярное выражение, либо праволинейная грамматика. Все три формализма (конечных автоматов, регулярных выражений и праволинейных грамматик) имеют одинаковую выразительную мощность. В частности, по регулярному выражению или праволинейной грамматике можно сконструировать конечный автомат, распознающий тот же язык.
Регулярные множества и выражения
Введем понятие регулярного множества, играющего важную роль в теории формальных языков.
Регулярное множество в алфавите T определяется рекурсивно следующим образом:
![]() (пустое множество) - регулярное множество в алфавите T;
(пустое множество) - регулярное множество в алфавите T;- {e} - регулярное множество в алфавите T (e - пустая цепочка);
- {a} - регулярное множество в алфавите T для каждого
![a in T]() ;
; - если P и Q - регулярные множества в алфавите T, то регулярными являются и множества
![P cup Q (объединение),]()
![PQ ; ( text{конкатенация, то есть множество} ; {pq ! mid ! p in P, ; q in Q})]()
![P^* ; (text{итерация:} ; P^*=bigcuplimits^infty_{n=0} ; P^n);]()
- ничто другое не является регулярным множеством в алфавите T.
Итак, множество в алфавите T регулярно тогда и только тогда, когда оно либо  , либо {e}, либо {a} для некоторого
, либо {e}, либо {a} для некоторого  , либо его можно получить из этих множеств применением конечного числа операций объединения, конкатенации и итерации.
, либо его можно получить из этих множеств применением конечного числа операций объединения, конкатенации и итерации.
Приведенное выше определение регулярного множества позволяет ввести следующую удобную форму его записи, называемую регулярным выражением.
Регулярное выражение в алфавите T и обозначаемое им регулярное множество в алфавите T определяются рекурсивно следующим образом:
![]() регулярное выражение, обозначающее регулярное множество
регулярное выражение, обозначающее регулярное множество ![]() ;
;- {e} - регулярное выражение, обозначающее регулярное множество {e};
- {a} - регулярное выражение, обозначающее регулярное множество {a};
- если p и q - регулярные выражения, обозначающие регулярные множества P и Q соответственно, то
- (p|q) - регулярное выражение, обозначающее регулярное множество
![P cup Q]() ,
, - (pq) - регулярное выражение, обозначающее регулярное множество PQ,
- (p*) - регулярное выражение, обозначающее регулярное множество P*;
- ничто другое не является регулярным выражением в алфавите T.
Мы будем опускать лишние скобки в регулярных выражениях, договорившись о том, что операция итерации имеет наивысший приоритет, затем идет операции конкатенации, наконец, операция объединения имеет наименьший приоритет.
Кроме того, мы будем пользоваться записью p+ для обозначения pp*. Таким образом, запись (a|((ba)(a*))) эквивалентна a|ba+.
Также, мы будем использовать запись L(r) для регулярного множества, обозначаемого регулярным выражением r.
Пример 3.1. Несколько примеров регулярных выражений и обозначаемых ими регулярных множеств:
- a(e|a)|b - обозначает множество {a; b; aa};
- a(a|b)* - обозначает множество всевозможных цепочек, состоящих из a и b, начинающихся с a;
- (a|b)*(a|b)(a|b)* - обозначает множество всех непустых цепочек, состоящих из a и b, то есть множество {a, b}+;
- ((0|1)(0|1)(0|1))* - обозначает множество всех цепочек, состоящих из нулей и единиц, длины которых делятся на 3.
Ясно, что для каждого регулярного множества можно найти регулярное выражение, обозначающее это множество, и наоборот. Более того, для каждого регулярного множества существует бесконечно много обозначающих его регулярных выражений.
Будем говорить, что регулярные выражения равны или эквивалентны (=), если они обозначают одно и то же регулярное множество.
Существуют алгебраические законы, позволяющие осуществлять эквивалентное преобразование регулярных выражений.
Лемма. Пусть p, q и r - регулярные выражения. Тогда справедливы следующие соотношения:
- p|q = q|p;
![]() * = e;
* = e;- p|(q|r) = (p|q)|r;
- p(qr) = (pq)r;
- p(q|r) = pq|pr;
- (p|q)r = pr|qr;
- pe = ep = p;
![]() p = p
p = p![]() =
= ![]() ;
;- p* = p|p*;
- (p*)* = p*;
- p|p = p;
- p|
![]() = p;
= p;
Следствие. Для любого регулярного выражения существует эквивалентное регулярное выражение, которое либо есть  , либо не содержит в своей записи
, либо не содержит в своей записи  .
.
В дальнейшем будем рассматривать только регулярные выражения, не содержащие в своей записи  . При практическом описании лексических структур бывает полезно сопоставлять регулярным выражениям некоторые имена, и ссылаться на них по этим именам. Для определения таких имен мы будем использовать запись вида
. При практическом описании лексических структур бывает полезно сопоставлять регулярным выражениям некоторые имена, и ссылаться на них по этим именам. Для определения таких имен мы будем использовать запись вида
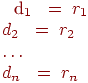
где di - различные имена, а каждое ri - регулярное выражение над символами  , то есть символами основного алфавита и ранее определенными символами (именами). Таким образом, для любого ri можно построить регулярное выражение над T, повторно заменяя имена регулярных выражений на обозначаемые ими регулярные выражения.
, то есть символами основного алфавита и ранее определенными символами (именами). Таким образом, для любого ri можно построить регулярное выражение над T, повторно заменяя имена регулярных выражений на обозначаемые ими регулярные выражения.
Пример 3.2. Несколько примеров использования имен для обозначения регулярных выражений.
- Регулярное выражение для множества идентификаторов.
![begin{aligned}& Letter = a mid b mid c mid ldots mid x mid y mid z\ & Digit=0 mid 1 mid ldots mid 9 \ & Identifier = Letter(Letter mid Digit)^*\ end{aligned}]()
- Регулярное выражение для множества чисел в десятичной записи.
![begin{aligned}& Digit=0 mid 1 mid ldots mid 9 \ & Integer=Digit^+\ & Fraction=.Integer mid e \ & Exponent= (E(+ mid - mid e)Integer) mid e \ & Number = Integer ; Fraction ; Exponent end{aligned}]()
Конечные автоматы
Регулярные выражения, введенные ранее, служат для описания регулярных множеств. Для распознавания регулярных множеств служат конечные автоматы. Недетерминированный конечный автомат (НКА) - по определению есть пятерка M = (Q, T, D, q0, F), где
- Q - конечное множество состояний,
- T - конечное множество допустимых входных символов (входной алфавит),
- D - функция переходов (отображающая множество
![Q times (T cup {e})]() во множество подмножеств множества Q), определяющая поведение управляющего устройства,
во множество подмножеств множества Q), определяющая поведение управляющего устройства, ![q_0 in Q]() - начальное состояние управляющего устройства,
- начальное состояние управляющего устройства,![F subseteq Q]() - множество заключительных состояний.
- множество заключительных состояний.
Работа конечного автомата представляет собой некоторую последовательность шагов, или тактов. Такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния и, возможно, сдвига входной головки на одну ячейку вправо (рис. 3.2.).
Недетерминизм автомата заключается в том, что, во- первых, находясь в некотором состоянии и обозревая текущий символ, автомат может перейти в одно из, вообще говоря, нескольких возможных состояний, и во-вторых, автомат может делать переходы по e.
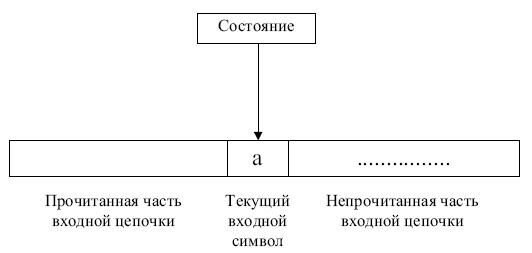
Рис. 3.2.
Пусть M = (Q, T, D, q0, F) - НКА. Конфигурацией автомата M называется пара  , где q - текущее состояние управляющего устройства, а w - цепочка символов на входной ленте, состоящая из символа под головкой и всех символов справа от него. Конфигурация (q0, w) называется начальной, а конфигурация (q, e), где
, где q - текущее состояние управляющего устройства, а w - цепочка символов на входной ленте, состоящая из символа под головкой и всех символов справа от него. Конфигурация (q0, w) называется начальной, а конфигурация (q, e), где  - заключительной (или допускающей). Тактом автомата M называется бинарное отношение
- заключительной (или допускающей). Тактом автомата M называется бинарное отношение  , определенное на конфигурациях M следующим образом: если
, определенное на конфигурациях M следующим образом: если  , где
, где  для всех
для всех  .
.
Будем обозначать символом  транзитивное (рефлексивно-транзитивное) замыкание отношения
транзитивное (рефлексивно-транзитивное) замыкание отношения  . Будем говорить, что автомат M допускает цепочку w, если
. Будем говорить, что автомат M допускает цепочку w, если  для некоторого
для некоторого  . Языком, допускаемым, (распознаваемым, определяемым) автоматом M, (обозначается L(M)), называется множество входных цепочек, допускаемых автоматом M. То есть,
. Языком, допускаемым, (распознаваемым, определяемым) автоматом M, (обозначается L(M)), называется множество входных цепочек, допускаемых автоматом M. То есть,
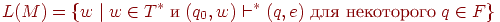
Важным частным случаем недетерминированного конечного автомата является детерминированный конечный автомат, который на каждом такте работы имеет возможность перейти не более чем в одно состояние и не может делать переходы по e.
Пусть M = (Q, T, D, q0, F) - НКА. Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия:
- D(q, e) =
![]() , для любого
, для любого ![q in Q]() , и
, и - D(q, a) содержит не более одного элемента для любых
![q in Q]() и
и ![a in T]() .
.
Так как функция переходов ДКА содержит не более одного элемента для любой пары аргументов, для ДКА мы будем пользоваться записью D(q, a)=p вместо D(q, a)={p}.
Конечный автомат может быть изображен графически в виде диаграммы, представляющей собой ориентированный граф, в котором каждому состоянию соответствует вершина, а дуга, помеченная символом  соединяет две вершины p и q, если
соединяет две вершины p и q, если  . На диаграмме выделяются начальное и заключительные состояния (в примерах ниже, соответственно, входящей стрелкой и двойным контуром).
. На диаграмме выделяются начальное и заключительные состояния (в примерах ниже, соответственно, входящей стрелкой и двойным контуром).
Пример 3.3. Пусть L = L(r), где r = (a|b)*a(a|b)(a|b).
- Недетерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4}, {a, b}, D, 1, {4}},
где функция переходов D определяется так:

Диаграмма автомата приведена на рис. 3.3 а.
- Детерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4, 5, 6, 7, 8}, {a, b}, D, 1, {3, 5, 6, 8}}
где функция переходов D определяется так:
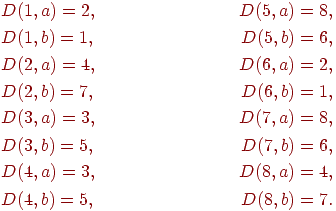
Диаграмма автомата приведена на рис. 3.3 б.
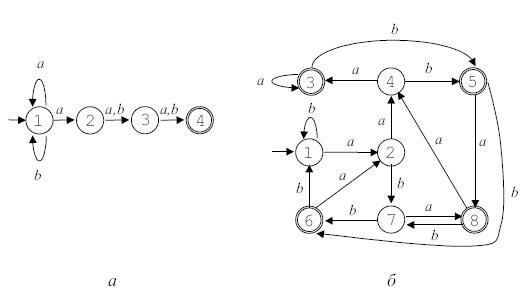
Рис. 3.3.
Пример 3.4. Диаграмма автомата, допускающего множество чисел в десятичной записи, приведена на рис. 3.4.
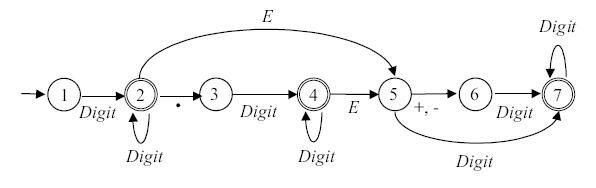
Рис. 3.4.
Пример 3.5. Анализ цепочек.
- При анализе цепочки w = ababa автомат из примера рис. 3.3, а, может сделать следующую последовательность тактов:
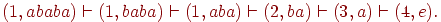
Состояние 4 является заключительным, отсюда, цепочка w допускается этим автоматом.
- При анализе цепочки w = ababab автомат из примера рис. 3.3, б, должен сделать следующую последовательность тактов:
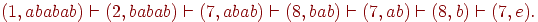
Так как состояние 7 не является заключительным, цепочка w не допускается этим автоматом.
Алгоритмы построения конечных автоматов
Построение недетерминированного конечного автомата по регулярному выражению
Рассмотрим алгоритм построения по регулярному выражению недетерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.1. Построение недетерминированного конечного автомата по регулярному выражению.
Вход. Регулярное выражение r в алфавите T.
Выход. НКА M, такой что L(M) = L(r).
Метод. Автомат для выражения строится композицией из автоматов, соответствующих подвыражениям. На каждом шаге построения строящийся автомат имеет в точности одно заключительное состояние, в начальное состояние нет переходов из других состояний и нет переходов из заключительного состояния в другие.
- Для выражения e строится автомат
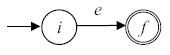
Рис. 3.5.
- Для выражения
![a (a in T)]() строится автомат
строится автомат - Пусть M(s) и M(t) - НКА для регулярных выражений s и t соответственно.
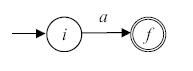
Рис. 3.6.
- Для выражения s|t автомат M(s|t) строится как показано на рис. 3.7. Здесь i - новое начальное состояние и f - новое заключительное состояние. Заметим, что имеет место переход по e из i в начальные состояния M(s) и M(t) и переход по e из заключительных состояний M(s) и M(t) в f. Начальное и заключительное состояния автоматов M(s) и M(t) не являются таковыми для автомата M(s|t).
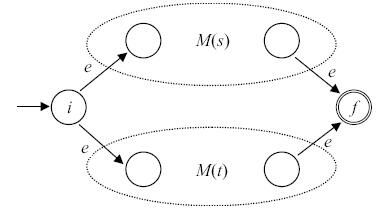
Рис. 3.7.
- Для выражения st автомат M(st) строится следующим образом:
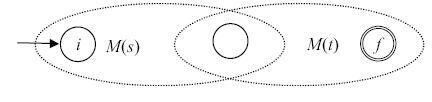
Рис. 3.8.
Начальное состояние автомата M(s) становится начальным для нового автомата, а заключительное состояние M(t) становится заключительным для нового автомата. Начальное состояние M(t) и заключительное состояние M(s) сливаются, то есть все переходы из начального состояния M(t) становятся переходами из заключительного состояния M(s). В новом автомате это объединенное состояние не является ни начальным, ни заключительным.
- Для выражения s* автомат M(s*) строится следующим образом:
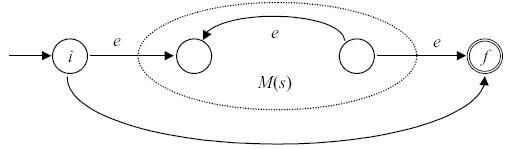
Рис. 3.9.
Здесь i - новое начальное состояние, а f - новое заключительное состояние.
Построение детерминированного конечного автомата по недетерминированному
Рассмотрим алгоритм построения по недетерминированному конечному автомату детерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.2. Построение детерминированного конечного автомата по недетерминированному.
Вход. НКА M = (Q, T, D, q0, F).
Выход. ДКА  .
.
Метод. Каждое состояние результирующего ДКА - это некоторое множество состояний исходного НКА.
В алгоритме будут использоваться следующие функции:  - множество состояний НКА, достижимых из состояний, входящих в R, посредством только переходов по e, то есть множество
- множество состояний НКА, достижимых из состояний, входящих в R, посредством только переходов по e, то есть множество
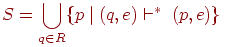
 - множество состояний НКА, в которые есть переход на входе a для состояний из R, то есть множество
- множество состояний НКА, в которые есть переход на входе a для состояний из R, то есть множество
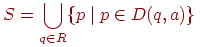
Вначале Q' и D' пусты. Выполнить шаги 1-4:
(1) Определить  .
.
(2) Добавить  в Q' как непомеченное состояние
в Q' как непомеченное состояние
(3) Выполнить следующую процедуру:

(4) Определить 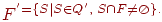
Пример 3.6. Результат применения алгоритма 3.2 приведен на рис. 3.10.
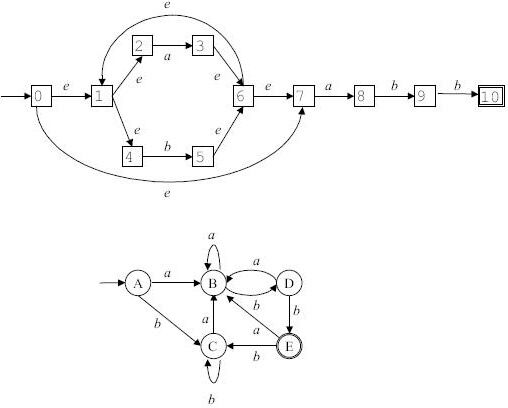
Рис. 3.10.
Построение детерминированного конечного автомата по регулярному выражению
Приведем теперь алгоритм построения по регулярному выражению детерминированного конечного автомата, допускающего тот же язык [?].
Пусть дано регулярное выражение r в алфавите T. К регулярному выражению r добавим маркер конца: (r)#. Такое регулярное выражение будем называть пополненным. В процессе своей работы алгоритм будет использовать пополненное регулярное выражение.
Алгоритм будет оперировать с синтаксическим деревом для пополненного регулярного выражения (r)# , каждый лист которого помечен символом  , а каждая внутренняя вершина помечена знаком одной из операций: • (конкатенация), | (объединение), * (итерация).
, а каждая внутренняя вершина помечена знаком одной из операций: • (конкатенация), | (объединение), * (итерация).
Каждому листу дерева (кроме e-листьев) присвоим уникальный номер, называемый позицией, и будем использовать его, с одной стороны, для ссылки на лист в дереве, и, с другой стороны, для ссылки на символ, соответствующий этому листу. Заметим, что если некоторый символ используется в регулярном выражении несколько раз, он имеет несколько позиций.
Обойдем дерево T снизу-вверх слева-направо и вычислим четыре функции: nullable,firstpos, lastpos и followpos. Три первые функции - nullable, firstpos и lastpos - определены на узлах дерева, а followpos - на множестве позиций. Значением всех функций, кроме nullable, является множество позиций. Функция followpos вычисляется через три остальные функции.
Функция firstpos(n) для каждого узла n синтаксического дерева регулярного выражения дает множество позиций, которые соответствуют первым символам в подцепочках, генерируемых подвыражением с вершиной в n. Аналогично, lastpos(n) дает множество позиций, которым соответствуют последние символы в подцепочках, генерируемых подвыражениями с вершиной n. Для узла n, поддеревья которого (то есть деревья, у которых узел n является корнем) могут породить пустое слово, определим nullable(n)=true, а для остальных узлов nullable(n)=false.
Таблица для вычисления функций nullable, firstpos и lastpos приведена на рис. 3.11.
Пример 3.7. На рис. 3.12 приведено cинтаксическое дерево для пополненного регулярного выражения (a|b)*abb# с результатом вычисления функций firstpos и lastpos. Слева от каждого узла расположено значение firstpos, справа от узла - значение lastpos. Заметим, что эти функции могут быть вычислены за один обход дерева.
Если i - позиция, то followpos(i) есть множество позиций j таких, что существует некоторая строка ... cd ..., входящая в язык, описываемый регулярным выражением, такая, что позиция i соответствует этому вхождению c, а позиция j - вхождению d.
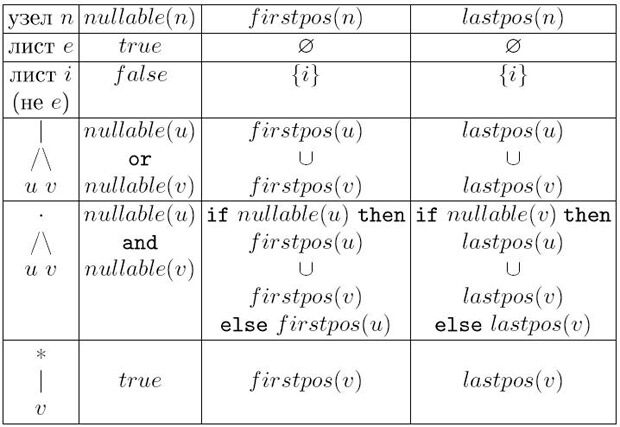
Рис. 3.11.

Рис. 3.12.

Рис. 3.13.
Функция followpos может быть вычислена также за один обход дерева снизу-вверх по таким двум правилам.
- Пусть n - внутренний узел с операцией • (конкатенация), u и v - его потомки. Тогда для каждой позиции i, входящей в lastpos(u), добавляем к множеству значений followpos(i) множество firstpos(v).
- Пусть n - внутренний узел с операцией * (итерация), u - его потомок. Тогда для каждой позиции i, входящей в lastpos(u), добавляем к множеству значений followpos(i) множество firstpos(u).
Пример 3.8. Результат вычисления функции followpos для регулярного выражения из предыдущего примера приведен на рис. 3.13.
Алгоритм 3.3. Прямое построение ДКА по регулярному выражению.
Вход. Регулярное выражение r в алфавите T.
Выход. ДКА M = (Q, T, D, q0, F), такой что L(M) = L(r).
Метод. Состояния ДКА соответствуют множествам позиций.
Вначале Q и D пусты. Выполнить шаги 1-6:
(1) Построить синтаксическое дерево для пополненного регулярного выражения (r)#.
(2) Обходя синтаксическое дерево, вычислить значения функций nullable, firstpos, lastpos и followpos.
(3) Определить q0 = firstpos(root), где root - корень синтаксического дерева.
(4) Добавить q0 в Q как непомеченное состояние.
(5) Выполнить следующую процедуру:

(6) Определить F как множество всех состояний из Q, содержащих позиции, связанные с символом #.
Пример 3.9. Результат применения алгоритма 3.3 для регулярного выражения (a|b)*abb приведен на рис. 3.14.
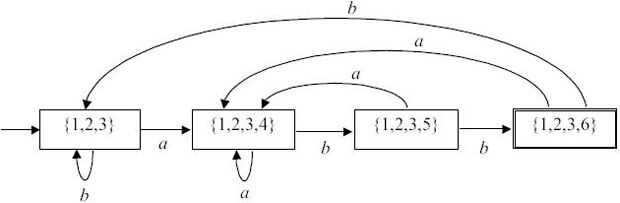
Рис. 3.14.
Построение детерминированного конечного автомата с минимальным числом состояний
Рассмотрим теперь алгоритм построения ДКА с минимальным числом состояний, эквивалентного данному ДКА [?].
Пусть M = (Q, T, D, q0, F) - ДКА. Будем называть M всюду определенным, если D(q, a) 
 , для всех
, для всех  и
и  .
.
Лемма. Пусть M = (Q, T, D, q0, F) - ДКА, не являющийся всюду определенным. Существует всюду определенный ДКА M', такой что L(M) = L(M').
Доказательство. Рассмотрим автомат
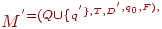
где q'  Q - некоторое новое состояние, а функция D' определяется следующим образом:
Q - некоторое новое состояние, а функция D' определяется следующим образом:
(1) Для всех  и
и  , таких что D(q, a)
, таких что D(q, a) 
 ,, определить D'(q, a) = D(q, a).
,, определить D'(q, a) = D(q, a).
(2) Для всех  и
и  , таких что D(q, a) =
, таких что D(q, a) =  , определить D'(q, a) = q'.
, определить D'(q, a) = q'.
(3) Для всех  определить D'(q', a) = q'.
определить D'(q', a) = q'.
Легко показать, что автомат M' допускает тот же язык, что и M.
Приведенный ниже алгоритм получает на входе всюду определенный автомат. Если автомат не является всюду определенным, его можно сделать таковым на основании только что приведенной леммы.
Алгоритм 3.4. Построение ДКА с минимальным числом состояний.
Вход. Всюду определенный ДКА M = (Q, T, D, q0, F).
Выход. ДКА  , такой что L(M) = L(M') и M' содержит наименьшее возможное число состояний.
, такой что L(M) = L(M') и M' содержит наименьшее возможное число состояний.
Метод. Выполнить шаги 1-5:
(1) Построить начальное разбиение ∏ множества состояний из двух групп: заключительные состояния Q и остальные Q - F, то есть ∏ = {F, Q - F}.
(2) Применить к ∏ следующую процедуру и получить новое разбиение ∏new:
for (каждой группы G в ∏){
разбить G на подгруппы так, чтобы
состояния s и t из G оказались
в одной подгруппе тогда и только тогда,
когда для каждого входного символа a
состояния s и t имеют переходы по a
в состояния из одной и той же группы в ∏,
заменить G в ∏new на множество всех
полученных подгрупп,
}
(3) Если ∏new = ∏, полагаем ∏res = ∏ и переходим к шагу 4, иначе повторяем шаг 2 с ∏ := ∏new.
(4) 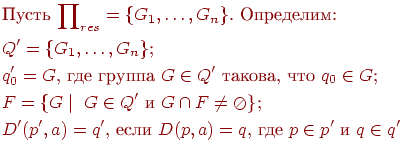
Таким образом, каждая группа в ∏res становится состоянием нового автомата M'. Если группа содержит начальное состояние автомата M, то эта группа становится начальным состоянием автомата M'. Если группа содержит заключительное состояние M, она становится заключительным состоянием M'. Отметим, что каждая группа ∏res либо состоит только из состояний из F, либо не имеет состояний из F. Переходы определяются очевидным образом.
(5) Если M' имеет "мертвое"состояние, то есть состояние, которое не является допускающим и из которого нет путей в допускающие, удалить его и связанные с ним переходы из M'. Удалить из M' также все состояния, недостижимые из начального.
Пример 3.10. Результат применения алгоритма 3.4 приведен на рис. 3.15.
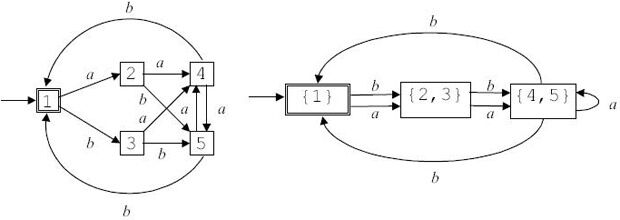
Рис. 3.15.
Связь регулярных множеств, конечных автоматов и регулярных грамматик
В разделе 3.3.3 приведен алгоритм построения детерминированного конечного автомата по регулярному выражению. Рассмотрим теперь как по описанию конечного автомата построить регулярное множество, совпадающее с языком, допускаемым конечным автоматом.
Теорема 3.1. Язык, допускаемый детерминированным конечным автоматом, является регулярным множеством.
Доказательство. Пусть L - язык, допускаемый детерминированным конечным автоматом
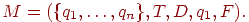
Введем De - расширенную функцию переходов автомата M: De(q, w) = p, где  , тогда и только тогда, когда
, тогда и только тогда, когда  .
.
Обозначим посредством  множество всех слов x таких, что De(qi, x) = qj и если De(qi, y) = qs для любой цепочки y - префикса x, отличного от x и e, то s
множество всех слов x таких, что De(qi, x) = qj и если De(qi, y) = qs для любой цепочки y - префикса x, отличного от x и e, то s  k.
k.
Иными словами,  есть множество всех слов, которые переводят конечный автомат из состояния qi в состояние qj , не проходя ни через какое состояние qs для s > k. Однако, i и j могут быть больше k.
есть множество всех слов, которые переводят конечный автомат из состояния qi в состояние qj , не проходя ни через какое состояние qs для s > k. Однако, i и j могут быть больше k.
 может быть определено рекурсивно следующим образом:
может быть определено рекурсивно следующим образом:
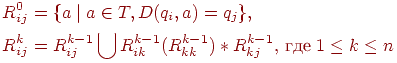
Таким образом, определение  означает, что для входной цепочки w, переводящей M из qi в qj без перехода через состояния с номерами, большими k, справедливо ровно одно из следующих двух утверждений:
означает, что для входной цепочки w, переводящей M из qi в qj без перехода через состояния с номерами, большими k, справедливо ровно одно из следующих двух утверждений:
- Цепочка w принадлежит
![R^{k-1}_{ij}]() , то есть при анализе цепочки w автомат никогда не достигает состояний с номерами, большими или равными k.
, то есть при анализе цепочки w автомат никогда не достигает состояний с номерами, большими или равными k. - Цепочка w может быть представлена как w = w1w2w3, где
![w_1 in R^{k-1}_{ik}]() (подцепочка w1 переводит M сначала в qk),
(подцепочка w1 переводит M сначала в qk), ![w_2 in (R^{k-1}_{kk} )^*]() (подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и
(подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и ![w_3 in R^{k-1}_{kj}]() (подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16.
(подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16.
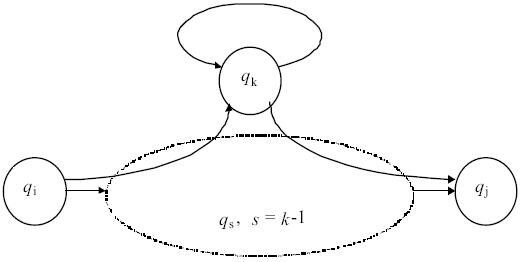
Рис. 3.16.
Тогда  . Индукцией по k можно показать, что это множество является регулярным.
. Индукцией по k можно показать, что это множество является регулярным.
Таким образом, для всякого регулярного множества имеется конечный автомат, допускающий в точности это регулярное множество, и наоборот - язык, допускаемый конечным автоматом есть регулярное множество.
Рассмотрим теперь соотношение между языками, порождаемыми праволинейными грамматиками и допускаемыми конечными автоматами.
Праволинейная грамматика G = (N, T, P, S) называется регулярной, если
(1) каждое ее правило, кроме S  e, имеет вид либо A
e, имеет вид либо A  aB, либо A
aB, либо A  a, где
a, где 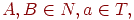
(2) в том случае, когда  , начальный символ S не встречается в правых частях правил.
, начальный символ S не встречается в правых частях правил.
Лемма. Пусть G - праволинейная грамматика. Существует регулярная грамматика G' такая, что L(G) = L(G').
Доказательство. Предоставляется читателю в качестве упражнения.
Теорема 3.2. Пусть G = (N, T, P, S) - праволинейная грамматика. Тогда существует конечный автомат M = (Q, T, D, q0, F) для которого L(M) = L(G).
Доказательство. На основании приведенной выше леммы, без ограничения общности можно считать, что G - регулярная грамматика.
Построим НКА M следующим образом:
- состояниями M будут нетерминалы G плюс новое состояние R, не принадлежащее N. Так что
![Q = N cup {R}]() ,
, - в качестве начального состояния M примем S, то есть q0 = S,
- если P содержит правило S
![]() e, то
e, то ![F = {S, R}]() , иначе F = {R}. Напомним, что S не встречается в правых частях правил, если
, иначе F = {R}. Напомним, что S не встречается в правых частях правил, если ![S rightarrow e in P]() ,
, - состояние
![R in D(A, a)]() , если
, если ![A rightarrow a in P]() . Кроме того, D(A, a) содержит все B такие, что
. Кроме того, D(A, a) содержит все B такие, что ![A rightarrow aB in P. ; ; D(R, a) = oslash]() , для каждого
, для каждого ![a in T]() .
.
M, читая вход w, моделирует вывод w в грамматике G. Покажем, что L(M) = L(G). Пусть  . Тогда
. Тогда  для некоторой последовательности нетерминалов A1, A2, ... , An-1. По определению, D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д., D(An-1, an) содержит R. Так что
для некоторой последовательности нетерминалов A1, A2, ... , An-1. По определению, D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д., D(An-1, an) содержит R. Так что  , поскольку De(S, w) содержит R, а
, поскольку De(S, w) содержит R, а  . Если
. Если  , то
, то  , так что e in L(M).
, так что e in L(M).
Аналогично, если  , то существует последовательность состояний S, A1, A2, ... , An-1, R такая, что D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д. Поэтому
, то существует последовательность состояний S, A1, A2, ... , An-1, R такая, что D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д. Поэтому  - вывод в G и
- вывод в G и  . Если
. Если  , то
, то  , так что
, так что  и
и  .
.
Теорема 3.3. Для каждого конечного автомата M = (Q, T, D, q0, F) существует праволинейная грамматика G = (N, T, P, S) такая, что L(G) = L(M).
Доказательство. Без потери общности можно считать, что автомат M - детерминированный. Определим грамматику G следующим образом:
- нетерминалами грамматики G будут состояния автомата M. Так что N = Q,
- в качестве начального символа грамматики G примем q0, то есть S = q0,
![A rightarrow aB in P]() , если D(A, a) = B,
, если D(A, a) = B,![A rightarrow a in P]() , если D(A, a) = B и
, если D(A, a) = B и ![B in F]() ,
, ![S rightarrow e in P]() , если
, если ![q_0 in F]() .
.
Доказательство того, что  тогда и только тогда, когда
тогда и только тогда, когда  , аналогично доказательству теоремы 3.2.
, аналогично доказательству теоремы 3.2.
В некоторых случаях для определения того, является ли язык регулярным, может быть полезным необходимое условие, которое называется леммой Огдена о разрастании.
Теорема 3.4. (Лемма о разрастании для регулярных множеств). Пусть L - регулярное множество. Существует такая константа k, что если  и
и  , то цепочку w можно представить в виде xyz, где
, то цепочку w можно представить в виде xyz, где  и
и  для всех
для всех  .
.
Доказательство. Пусть M = (Q, Σ, D, q0, F) - конечный автомат, допускающий L, то есть L(M) = L и k = |Q|. Пусть  и
и  . Рассмотрим последовательность конфигураций, которые проходит автомат M, допуская цепочку w. Так как в ней по крайней мере k + 1 конфигурация, то среди первых k+1 конфигурации найдутся две с одинаковыми состояниями. Таким образом, получаем существование такой последовательности тактов, что
. Рассмотрим последовательность конфигураций, которые проходит автомат M, допуская цепочку w. Так как в ней по крайней мере k + 1 конфигурация, то среди первых k+1 конфигурации найдутся две с одинаковыми состояниями. Таким образом, получаем существование такой последовательности тактов, что
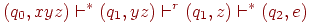
для некоторых  . Отсюда
. Отсюда  . Но тогда для любого i > 0 автомат может проделать последовательность тактов
. Но тогда для любого i > 0 автомат может проделать последовательность тактов  Таким образом,
Таким образом,  для всех i
для всех i  1. Случай i = 0 то есть
1. Случай i = 0 то есть  также очевиден.
также очевиден.
С помощью леммы о разрастании можно показать, что не является регулярным множеством язык L={0n1n|n 1}.
1}.
Допустим, что L регулярен. Тогда для достаточно большого n0n1n можно представить в виде xyz, причем y  e и
e и  для всех i
для всех i  0. Если
0. Если  или
или  , то
, то  . Если
. Если  , то
, то  . Получили противоречие. Следовательно, L не может быть регулярным множеством.
. Получили противоречие. Следовательно, L не может быть регулярным множеством.
Программирование лексического анализа
Как уже отмечалось ранее, лексический анализатор (ЛА) может быть оформлен как подпрограмма. При обращении к ЛА, вырабатываются как минимум два результата: тип выбранной лексемы и ее значение (если оно есть).
Если ЛА сам формирует таблицы объектов, он выдает тип лексемы и указатель на соответствующий вход в таблице объектов. Если же ЛА не работает с таблицами объектов, он выдает тип лексемы, а ее значение передается, например, через некоторую глобальную переменную. Помимо значения лексемы, эта глобальная переменная может содержать некоторую дополнительную информацию: номер текущей строки, номер символа в строке и т.д. Эта информация может использоваться в различных целях, например, для диагностики.
В основе ЛА лежит диаграмма переходов соответствующего конечного автомата. Отдельная проблема здесь - анализ ключевых слов. Как правило, ключевые слова - это выделенные идентификаторы. Поэтому возможны два основных способа распознавания ключевых слов: либо очередная лексема сначала диагностируется на совпадение с каким-либо ключевым словом и в случае неуспеха делается попытка выделить лексему из какого-либо класса, либо, наоборот, после выборки лексемы идентификатора происходит обращение к таблице ключевых слов на предмет сравнения. Подробнее о механизмах поиска в таблицах будет сказано ниже (гл. "Организация таблиц символов "), здесь отметим только, что поиск ключевых слов может вестись либо в основной таблице имен и в этом случае в нее до начала работы ЛА загружаются ключевые слова, либо в отдельной таблице. При первом способе все ключевые слова непосредственно встраиваются в конечный автомат ЛА, во втором конечный автомат содержит только разбор идентификаторов.
В некоторых языках (например, ПЛ/1 или Фортран) ключевые слова могут использоваться в качестве обычных идентификаторов. В этом случае работа ЛА не может идти независимо от работы синтаксического анализатора. В Фортране возможны, например, следующие строки:
DO 10 I=1,25
DO 10 I=1.25
В первом случае строка - это заголовок цикла DO, во втором - оператор присваивания. Поэтому, прежде чем можно будет выделить лексему, ЛА должен заглянуть довольно далеко. Еще сложнее дело в ПЛ/1. Здесь возможны такие операторы:
IF ELSE THEN ELSE = THEN, ELSE THEN = ELSE,
или
DECLARE (A1, A2, ... , AN)
и только в зависимости от того, что стоит после ")", можно определить, является ли DECLARE ключевым словом или идентификатором. Длина такой строки может быть сколь угодно большой и уже невозможно отделить фазу синтаксического анализа от фазы лексического анализа.
Рассмотрим несколько подробнее вопросы программирования ЛА. Основная операция ЛА, на которую уходит большая часть времени его работы - это взятие очередного символа и проверка на принадлежность его некоторому диапазону. Например, основной цикл при выборке числа в простейшем случае может выглядеть следующим образом:
while (Insym <='9' && Insym>='0')
{ ... }
Программу можно значительно улучшить следующим образом [5]. Пусть LETTER, DIGIT, BLANK - элементы перечислимого типа. Введем массив map, входами которого будут символы, значениями - типы символов. Инициализируем массив map следующим образом:
map['a']=LETTER,
........
map['z']=LETTER,
map['0']=DIGIT,
........
map['9']=DIGIT,
map[' ']=BLANK,
........
Тогда приведенный цикл примет следующую форму:
while (map[Insym]==DIGIT)
{ ... }
Выделение ключевых слов может осуществляться после выделения идентификаторов. ЛА работает быстрее, если ключевые слова выделяются непосредственно.
Для этого строится конечный автомат, описывающий множество ключевых слов. На рис. 3.17 приведен фрагмент такого автомата.
Рассмотрим пример программирования этого конечного автомата на языке Си, приведенный в [17]:
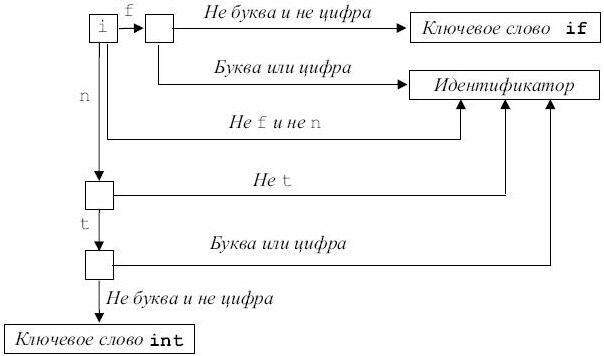
Рис. 3.17.
........
case 'i':
if (cp[0]=='f' &&!(map[cp[2]] & (DIGIT | LETTER)))
{cp++, return IF,}
if (cp[0]=='n' && cp[1]=='t'
&&!(map[cp] & (DIGIT | LETTER)))
{cp+=2, return INT,}
{ обработка идентификатора }
........
Здесь cp - указатель текущего символа. В массиве map классы символов кодируются битами.
Поскольку ЛА анализирует каждый символ входного потока, его скорость существенно зависит от скорости выборки очередного символа входного потока. В свою очередь, эта скорость во многом определяется схемой буферизации. Рассмотрим возможные эффективные схемы буферизации.
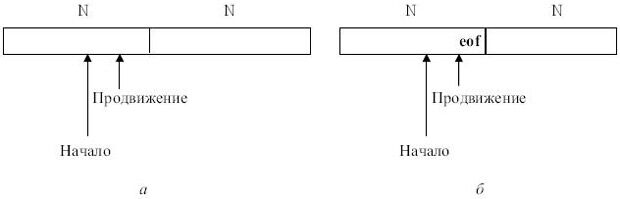
Рис. 3.18.
Будем использовать буфер, состоящий из двух одинаковых частей длины N (рис. 3.18, а), где N - размер блока обмена (например, 1024, 2048 и т.д.). Чтобы не читать каждый символ отдельно, в каждую из половин буфера поочередно одной командой чтения считывается N символов. Если на входе осталось меньше N символов, в буфер помещается специальный символ (eof). На буфер указывают два указателя: продвижение и начало. Между указателями размещается текущая лексема. Вначале они оба указывают на первый символ выделяемой лексемы. Один из них, продвижение, продвигается вперед, пока не будет выделена лексема, и устанавливается на ее конец. После обработки лексемы оба указателя устанавливаются на символ, следующий за лексемой. Если указатель продвижение переходит середину буфера, правая половина заполняется новыми N символами. Если указатель продвижение переходит правую границу буфера, левая половина заполняется N символами и указатель продвижение устанавливается на начало буфера.
При каждом продвижении указателя необходимо проверять, не достигли ли мы границы одной из половин буфера. Для всех символов, кроме лежащих в конце половин буфера, требуются две проверки. Число проверок можно свести к одной, если в конце каждой половины поместить дополнительный _сторожевойї символ, в качестве которого логично взять eof (рис. 3.18, б).
В этом случае почти для всех символов делается единственная проверка на совпадение с eof и только в случае совпадения нужно дополнительно проверить, достигли ли мы середины или правого конца.
Конструктор лексических анализаторов LEX
Для автоматизации разработки ЛА было создано довольно много средств. Как правило, входным языком для них служат или праволинейные грамматики, или язык регулярных выражений. Одной из наиболее распространенных систем является LEX, работающий с расширенными регулярными выражениями. LEX-программа состоит из трех частей:
Объявления
%%
Правила трансляции
%%
Вспомогательные подпрограммы Секция объявлений включает объявления переменных, констант и определения регулярных выражений. При определении регулярных выражений могут использоваться следующие конструкции:
| [abc] | - либо a, либо b, либо c, |
| [a-z] | - диапазон символов, |
| R* | - 0 или более повторений регулярного выражения R, |
| R+ | - 1 или более повторений регулярного выражения R, |
| R1/R2 | - R1, если за ним следует R2, |
| R1|R2 | - либо R1, либо R2, |
| R? | - если есть R, выбрать его, |
| R$ | - выбрать R, если оно последнее в строке, |
| ^R | - выбрать R, если оно первое в строке, |
| [^R] | - дополнение к R, |
| R{n,m} | - повторение R от n до m раз, |
| {имя} | - именованное регулярное выражение, |
| (R) | - группировка. |
Правила трансляции LEX-программ имеют вид
p_1 { действие_1 }
p_2 { действие_2 }
................
p_n { действие_n }
где p_i - регулярное выражение, а действие_i - фрагмент программы, описывающий, какое действие должен сделать ЛА, когда образец p_i сопоставляется лексеме. В LEX действия записываются на Си.
Третья секция содержит вспомогательные процедуры, необходимые для действий. Эти процедуры могут транслироваться раздельно и загружаться с ЛА.
ЛА, сгенерированный LEX, взаимодействует с синтаксическим анализатором следующим образом. При вызове его синтаксическим анализатором ЛА посимвольно читает остаток входа, пока не находит самый длинный префикс, который может быть сопоставлен одному из регулярных выражений p_i. Затем он выполняет действие_i. Как правило, действие_i возвращает управление синтаксическому анализатору. Если это не так, то есть в соответствующем действии нет возврата, то ЛА продолжает поиск лексем до тех пор, пока действие не вернет управление синтаксическому анализатору. Повторный поиск лексем вплоть до явной передачи управления позволяет ЛА правильно обрабатывать пробелы и комментарии.
Синтаксическому анализатору ЛА возвращает единственное значение - тип лексемы. Для передачи информации о типе лексемы используется глобальная переменная yylval. Текстовое представление выделенной лексемы хранится в переменной yytext, а ее длина в переменной yylen.
Пример 3.11. LEX-программа для ЛА, обрабатывающего идентификаторы, числа, ключевые слова if, then, else и знаки логических операций.
%{ /*определения констант LT,LE,EQ,NE,GT,
GE,IF,THEN,ELSE,ID,NUMBER,RELOP, например,
через DEFINE или скалярный тип*/ %}
/*регулярные определения*/
delim [ tn]
ws {delim}+
letter [A-Za-z]
digit [0-9]
id {letter}({letter}|{digit})*
number {digit}+(.{digit}+)?,(E[+-]?;,{digit}+)?;,
%%
{ws} {/* действий и возврата нет */}
if {return(IF),}
then {return(THEN),}
else {return(ELSE),}
{id} {yylval=install_id(), return(ID),}
{number} {yylval=install_num(), return(NUMBER),}
"<" {yylval=LT, return(RELOP),}
"<=" {yylval=LE, return(RELOP),}
"=" {yylval=EQ, return(RELOP),}
"<>" {yylval=NE, return(RELOP),}
">" {yylval=GT, return(RELOP),}
">=" {yylval=GE, return(RELOP),}
%%
install_id()
{/*подпрограмма, которая помещает лексему,
на первый символ которой указывает yytext,
длина которой равна yylen, в таблицу
символов и возвращает указатель на нее*/
}
install_num()
{/*аналогичная подпрограмма для размещения
лексемы числа*/
}
В разделе объявлений, заключенном в скобки %{ и %}, перечислены константы, используемые правилами трансляции. Все, что заключено в эти скобки, непосредственно копируется в программу ЛА lex.yy.c и не рассматривается как часть регулярных определений или правил трансляции. То же касается и вспомогательных подпрограмм третьей секции. В данном примере это подпрограммы install_id и install_num.
В секцию определений входят также некоторые регулярные определения. Каждое такое определение состоит из имени и регулярного выражения, обозначаемого этим именем. Например, первое определенное имя - это delim. Оно обозначает класс символов { tn}, то есть любой из трех символов: пробел, табуляция или новая строка. Второе определение - разделитель, обозначаемый именем ws. Разделитель - это любая последовательность одного или более символов-разделителей. Слово delim должно быть заключено в скобки, чтобы отличить его от образца, состоящего из пяти символов delim.
В определении letter используется класс символов. Сокращение [A-Za-z] означает любую из прописных букв от A до Z или строчных букв от a до z. В пятом определении для id для группировки используются скобки, являющиеся метасимволами LEX. Аналогично, вертикальная черта - метасимвол LEX, обозначающий объединение.
В последнем регулярном определении number символ "+" используется как метасимвол "одно или более вхождений", символ "?" как метасимвол "ноль или одно вхождение". Обратная черта используется для того, чтобы придать обычный смысл символу, использующемуся в LEX как метасимвол. В частности, десятичная точка в определении number обозначается как "", поскольку точка сама по себе представляет класс, состоящий из всех символов, за исключением символа новой строки. В классe символов [+] обратная черта перед минусом стоит потому, что знак минус используется как символ диапазона, как в [A-Z].
Если символ имеет смысл метасимвола, то придать ему обычный смысл можно и по-другому, заключив его в кавычки. Так, в секции правил трансляции шесть операций отношения заключены в кавычки.
Лекция "Физиология и гигиена системы выделения" также может быть Вам полезна.
Рассмотрим правила трансляции, следующие за первым %%. Согласно первому правилу, если обнаружено ws, то есть максимальная последовательность пробелов, табуляций и новых строк, никаких действий не производится. В частности, не осуществляется возврат в синтаксический анализатор.
Согласно второму правилу, если обнаружена последовательность букв "if", нужно вернуть значение IF, которое определено как целая константа, понимаемая синтаксическим анализатором как лексема "if". Аналогично обрабатываются ключевые слова "then" и "else" в двух следущих правилах.
В действии, связанном с правилом для id, два оператора. Переменной yylval присваивается значение, возвращаемое процедурой install_id. Переменная yyl- val определена в программе lex.yy.c, выходе LEX, и она доступна синтаксическому анализатору. yylval хранит возвращаемое лексическое значение, поскольку второй оператор в действии, return(ID), может только возвратить код класса лексем. Функция install_id заносит идентификаторы в таблицу символов.
Аналогично обрабатываются числа в следующем правиле. В последних шести правилах yylval используется для возврата кода операции отношения, возвращаемое же функцией значение - это код лексемы relop.
Если, например, в текущий момент ЛА обрабатывает лексему "if", то этой лексеме соответствуют два образца: "if" и {id} и более длинной строки, соответствующей образцу, нет. Поскольку образец "if" предшествует образцу для идентификатора, конфликт разрешается в пользу ключевого слова. Такая стратегия разрешения конфликтов позволяет легко резервировать ключевые слова.
Если на входе встречается "<=", то первому символу соответствует образец <, но это не самый длинный образец, который соответствует префиксу входа. Стратегия выбора самого длинного префикса легко разрешает такого рода конфликты.

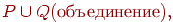

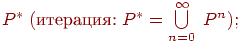
 ,
,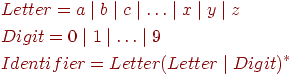
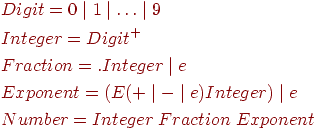
 во множество подмножеств множества Q), определяющая поведение управляющего устройства,
во множество подмножеств множества Q), определяющая поведение управляющего устройства, - начальное состояние управляющего устройства,
- начальное состояние управляющего устройства, - множество заключительных состояний.
- множество заключительных состояний. строится автомат
строится автомат , то есть при анализе цепочки w автомат никогда не достигает состояний с номерами, большими или равными k.
, то есть при анализе цепочки w автомат никогда не достигает состояний с номерами, большими или равными k. (подцепочка w1 переводит M сначала в qk),
(подцепочка w1 переводит M сначала в qk),  (подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и
(подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и  (подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16.
(подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16. ,
, , иначе F = {R}. Напомним, что S не встречается в правых частях правил, если
, иначе F = {R}. Напомним, что S не встречается в правых частях правил, если  , если
, если  . Кроме того, D(A, a) содержит все B такие, что
. Кроме того, D(A, a) содержит все B такие, что  , для каждого
, для каждого  , если D(A, a) = B,
, если D(A, a) = B, ,
,  .
.

















