Машинные коды двоичного числа

Машинные коды двоичного числа

В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства ЭВМ, выполняющие арифметические операции.

Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.

Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.

Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.

Прямой код

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль для положительных чисел или единица для отрицательных чисел) перед его старшим числовым разрядом.

Цифровые разряды прямого кода содержат модуль представляемого числа, что обеспечивает наглядность представления чисел в прямом коде (ПК).

Пример. Записать прямой код чисел  и

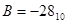
Рекомендуемые материалы

Решение: Рассмотрим однобайтовое представление двоичного числа.

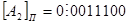
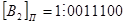
В прямом коде нуль имеет двоякое изображение:  – положительный ноль,  – отрицательный ноль.

В общем случае ОК является дополнением модуля исходного числа до наибольшего числа без знака, помещенного в разрядную сетку.

Обратный код

В обратном коде (ОК), также как и в прямом коде, для обозначения знака положительного числа используется бит, равный нулю, и знака отрицательного – единице.

Обратный код положительного двоичного числа совпадает с его прямым кодом. Обратный код отрицательного двоичного числа содержит единицу в знаковом разряде, формируется дополнением модуля исходного числа нулями до самого старшего разряда модуля, а затем поразрядной заменой всех нулей числа на единицу и всех единиц на нули. Обратный перевод осуществляется в той же последовательности.

Пример. Записать обратный код чисел  и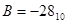

Решение:

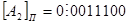
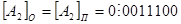
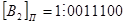
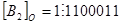
Работа с обратным кодом вызывает ряд трудностей. В частности, возникают два нуля: положительный и отрицательный, т.е. в прямом коде (в котором представлены положительные числа) имеет место , а в обратном коде (в котором представлены отрицательные числа) .

Дополнительный код

Дополнительный код (ДК) строится следующим образом.

Дополнительный код положительного двоичного числа совпадает с его прямым кодом. Для отрицательных двоичных чисел сначала формируется обратный код (ОК), а затем к младшему разряду (МЗР) прибавляют 1. Обратный перевод ДК в ПК осуществляется аналогичными операциями в той же последовательности.

Пример. Записать дополнительный код чисел  и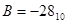

Решение:

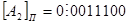
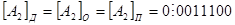
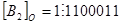
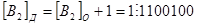
Использование ДК для представления отрицательных чисел устраняет двусмысленное представление нулевого результата (возникновение двух нулей: положительного и отрицательного), так как отрицательный ноль исчезает.

В общем случае использованием ДК для записи отрицательных чисел можно перекрыть диапазон десятичных чисел от –2^k-1 до +2^k-1-1, где k – число используемых двоичных разрядов, включая знаковый. Так, с помощью одного байта можно представить десятичные числа от  до , либо только положительные числа от 0 до 255 (здесь под положительными числами понимаются числа без знака). Оба этих способа представления чисел (со знаком и без знака) широко используются в ЭВМ.

В ЭВМ используется быстрый способ формирования ДК. Его суть заключается в следующем. Двоичное число в ПК просматривается от младшего значащего разряда к старшему. Пока встречаются нули, их копируют в одноименные разряды результата. Первая встретившаяся единица также копируется в соответствующий разряд, а каждый последующий бит исходного числа заменяется на противоположный (0 – на 1, 1 – на 0).

Пример. Записать дополнительный код числа  двумя способами.

Решение:

1 способ (быстрый).

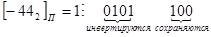
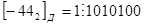
2 способ.

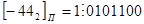
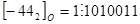
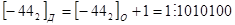
Как видно, результаты, полученные при преобразовании обоими методами, совпадают.

Модифицированные обратные и дополнительные коды

Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак «+» в этих кодах обозначается двумя нулевыми разрядами, а «–» – двумя единичными разрядами. Целью введения модифицированных кодов являются фиксация и обнаружение случаев переполнения разрядной сетки. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов «01» свидетельствует о положительном переполнении разрядной сетки, а «10» - об отрицательном переполнении.

Лекция "6. Информационный рынок" также может быть Вам полезна.

Вопросы для самопроверки:

1. Дайте определение системы счисления. Какие системы счисления Вы знаете?

2. Сформулируйте правило перевода целых чисел из одной системы счисления в другую.

3. Сформулируйте правило перевода дробных чисел из одной системы счисления в другую.

4. В чем особенность перевода чисел из восьмеричной (шестнадцатеричной) системы счисления в двоичную и наоборот?

5. Сформулируйте правило формирования прямого, обратного и дополнительного кодов двоичного числа.