Преобразование координат в двумерной системе

Перенос точки А на заданный вектор U иллюстрируется ниже приведенным рисунком (Рис. 5.1‑2). Решение задачи рассматриваемого преобразования сводится к определению на основании старых координат новых координат заданной точки после ее перенесения на заданный вектор

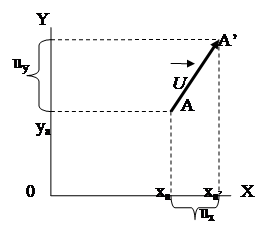Рис. 5.1‑2

Из приведенного рисунка видно, что новые координаты точки после рассматриваемого преобразования рассчитываются следующим образом:

x_a_’= x_a + u_x;

y_a_’= y_a + u_y. (5.1-1)

Перенос системы координат на заданный вектор

Перенос системы координат на заданный вектор U иллюстрируется следующим рисунком (Рис. 1.1‑3).

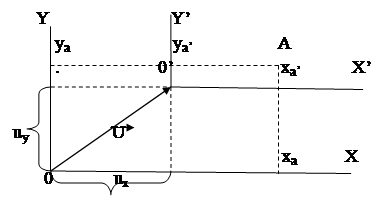Рис. 5.1‑3

Координатные оси после перенесения системы обозначены как X’,Y’.

Из рисунка видно, что координаты точки А в новой системе координат X’0’Y’ будут определяться как:

x_a’ = x_a - u_x;

y_a’ = y_a – u_y. (5.1-2)

Сравнив выражение (5.1-1) и (5.1-2), можно сделать вывод, что преобразование типа «перенос системы координат на вектор U » эквивалентно обратному преобразованию типа «перенос точки на вектор U » (т.е. переносу точки на вектор –U).

Зеркальное отображение положения точки относительно координатной оси.

Зеркальное отображение точки А относительно координатных осей X и Y приведено на Рис. 1.1‑4.

Новые координаты при этих преобразовании определяются следующим образом.

Рис. 5.1‑4

При зеркальном отображении относительно оси Y (Рис. 1.1‑4a) имеем:

x_a_’=- x_a.

При зеркальном отображении относительно оси X (Рис. 1.1‑4 b) имеем:

y_a_’=- y_a.

Смена направление осей координат иллюстртруется ниже приведенным рисунком (Рис. 5.1‑5).

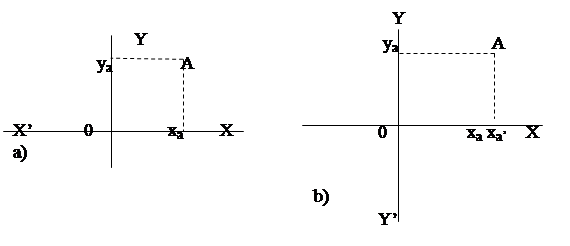Рис. 5.1‑5

Новое положение координатных осей X, Y на рисунке обозначено как X’, Y’.

Смена направленности оси X иллюстрируется на Рис. 5.1‑5a).

Как видно из рисунка, данное преобразование предполагает нахождение новых координат точки следующим образом.

x_a_’=- x_a.

При смене направленности оси Y (Рис. 5.1‑5b) имеем:

y_a_’=- y_a.

Изменение масштабов по координатным осям предполагает следующие преобразования координат точки A:

x_a’= n x_a;

y_a’= m y_a,

где n и m - вводимые масштабные коэффициенты, соответственно, по координатным осям X и Y.

Поворот точки относительно начала координат.

Данное преобразование, предполагающее поворот точки на заданный угол относительно начала координат, иллюстрируется ниже приведенным рисунком (Рис. 1.1‑6).

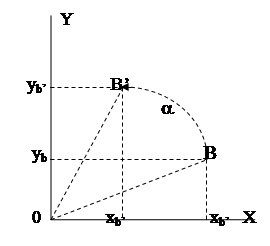Рис. 5.1‑6

На приведенном рисунке приняты следующие обозначения:

- B,B’ – соответственно, старое и новое положение точки при повороте относительно начала координат;

- a- угол поворота.

Очевидно, что новые координаты в общем случае ищутся согласно соотношениям:

x_b_’= c x_b+ d y_b; (5.1-3)

y_b_’= e x_b+ f y_b. (5.1-4)

Для нахождения коэффициентов c,d,e,f этих выражений рассмотрим два частных случая.

Рассмотрим сначала поворот на заданный угол a единичного вектора по координатной оси X (Рис. 1.1‑7).

Рис. 5.1‑7

Новые координаты единичного вектора U после поворота на угол a определяются следующим образом:

x_v’= 1*cos a= c x_b+ d y_b= c*1 + d*0,

откуда с = cos a;

y_v’= 1*sin a = e x_b+ d y_b= e*1+f*0,

откуда e = sin a.

Рассмотрим теперь поворот на заданный угол единичного вектора U по оси Y (Рис. 1.1‑8).

Новые координаты вектора U после поворота на угол a определяются следующим образом:

x_U_’= -1*sin a= c x_U+ d y_U= c*0 + d*1,

откуда d = -sin a;

y_U_’= 1*sin a = e x_U+ d y_U= e*1+f*0,

откуда e = sin a.

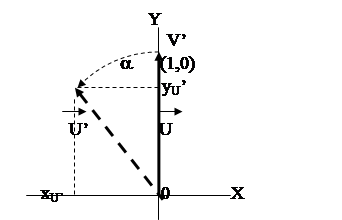координатной оси y ().

Рис. 5.1‑8

Подставив полученные значения для коэффициентов в выражение (5.1-3) и (5.1-4), будем иметь аналитические выражения для расчета новых значений

координат для преобразования типа поворота относительно начала координат:

x_b_’= x_b cos a - y_b sin a; (5.1-5)

y_b’= x_b sin a + y_b cos a. (5.1-6)

Легко показать, что преобразование типа поворота системы координат относительно ее начала соответствует обратному преобразованию типа «поворот точки относительно начала координат».

Сложные преобразования координат

Сложные преобразования координат реализуются через соответствующую последовательность базовых преобразований.

Для примера рассмотрим преобразования, имеющие место при повороте точки относительно произвольного вектора U.

Заданное преобразование иллюстрируется ниже приведенным рисунком (Рис. 5.1‑9).

Рис. 5.1‑9

Заданное преобразование можно выполнить, реализовав три следующие базовые преобразования.

1. Перенос начало исходной системы координат в точку, принадлежащую заданному вектор (например, начальную точку вектора).

2. Поворот в новой системе координат точки на заданный угол.

3. Возврат в исходную систему координат.

На Рис. 1.1‑10 приведена последовательность описанных базовых преобразований.

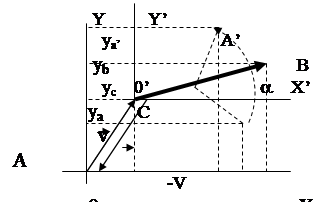Рис. 5.1‑10

Исходная система координат перемещается на вектор V и образуется новая система координат X’0’Y’, в которой заданный поворот является базовым поворотом относительно начала новой системы координат X’0’Y’.

Координаты заданной точки A в новой системе координат рассчитываются как:

x_a’= x_a - v_x= x_a - x_c;

y_a’= y_a - v_y= y_a - y_c.

Заданный поворот является базовым поворотом в новой системы координат X’0’Y’, поэтому для координат точки после поворота на угол a относительно точки 0’, используя уравнения (5.1-4) и (5.1-5), будем иметь:

x_a_’’= x_a_’ cosa - y_a_’sina= (x_a -x_c)cosa-(y_a -y_c) sina;

y_a_’’= x_a_’ sina - y_a_’cosa= (x_a -x_c) sina + (y_a -y_c) cosa.

После выполнения поворота относительно заданного вектора, система координат перемещается на вектор –V, т.е. осуществляется возврат в заданную систему координат X0Y. Координаты точки ищутся как:

x_a_’’’= x_a_’’ + x_c = (x_a - x_c) cosa - (y_a - y_c) sina + x_c;

y_a’”= y_a’’ + y_c = (x_a - x_c) sina + (y_a - y_c) cosa. + y_c .

Базовые преобразования удобно представлять в виде матриц. В этом случае последовательности базовых преобразований, реализующих сложное преобразование, представляется в виде произведения соответствующих матриц базовых преобразований.

Соотношения новых и старых координат при повороте на угол a относительно начала координат, в матричной форме могут быть представлены в виде:

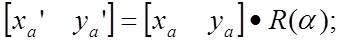
где:

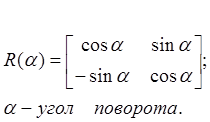
Обратное преобразование рассматриваемого поворота будет задаваться с помощью матрицы:

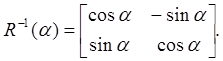
Преобразования типа «перенос точки на вектор» нельзя отобразить с помощью матриц, размерностью «два на два». Но для этого преобразования также можно использовать матричную форму, если представить координаты точки в однородной системе координат:

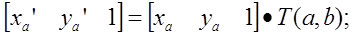
где:

a,b- параметры вектора переноса.

Обратное преобразование типа переноса задается в виде матрицы:

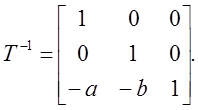
Матрица смены направленности оси X имеет вид:

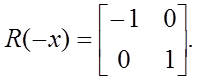
Матрица зеркального отображения точки относительно координаты Y имеет точно такой вид.

Матрица смены направленности оси Y имеет вид:

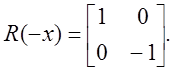
Матрица зеркального отображения точки относительно координаты X имеет точно такой вид.

Матрица изменения масштабов по координатным осям имеет вид:

Люди также интересуются этой лекцией: 3.3 Построение модели изучаемой системы.

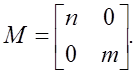
- где n и m - вводимые масштабные коэффициенты, соответственно, по координатным осям X и Y.

Преобразование типа «поворот относительно произвольного вектора», начало которого находится в точке (a,b,c), можно реализовать в матричной форме следующим образом:

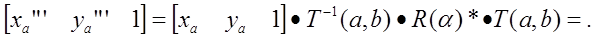
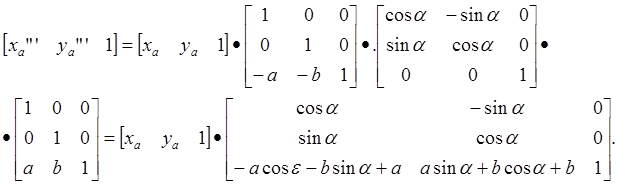
Обозначение матрицы знаком «*» означает использование расширенной матрицы. В выше приведенном выражении матрица R(a), соответствующая повороту относительно начала координат, берется в расширенной форме (добавлены одна колонка и одна строка, имеющие все нулевые элементы, кроме элемента на их пересечении, который равен «1»).

Поделитесь ссылкой:

Популярные услуги

Преобразование координат в двумерной системе

Рекомендуемые материалы

Рекомендуемые лекции