Проектирование нечётких алгоритмов управления

Лекция № 6. ПРОЕКТИРОВАНИЕ НЕЧЕТКИХ АЛГОРИТМОВ УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ

Общие принципы построения интеллектуальных систем управления на основе нечеткой логики

Как уже отмечалось выше, применение нечеткой логики обеспечивает принципиально новый подход к проектированию систем управления, "прорыв" в новые информационные технологии, гарантирует возможность решения широкого круга проблем, в которых данные, цели и ограничения являются слишком сложными или плохо определенными и в силу этого не поддаются точному математическому описанию.

Возможны различные ситуации, в которых могут использоваться нечеткие модели динамических систем:

- когда имеется некоторое лингвистическое описание, которое отражает качественное понимание (представление) процесса и позволяет непосредственно построить множество нечетких логических правил;

- имеются известные уравнения, которые (хотя бы грубо) описывают поведение управляемого процесса, но параметры этих уравнений не могут быть точно идентифицированы;

- известные уравнения, описывающие процесс, являются слишком сложными, но они могут быть интерпретированы нечетким образом для построения лингвистической модели;

- с помощью входных/выходных данных оцениваются нечеткие логические правила поведения системы.

Первые результаты практического применения алгоритмов нечеткой логики к управлению реальными техническими объектами были опубликованы в 1974 г. в работах профессора Лондонского Королевского колледжа Э.Х. Мамдани, посвященных проблеме регулирования парогенератора для электростанции. В этих работах была предложена ставшая сегодня классической структурная схема системы нечеткого управления (рис. 3.1).

Рекомендуемые материалы

Под нечетким управлением (Fuzzy Control) в данном, случае понимается стратегия управления, основанная на эмпирически приобретенных знаниях относительно функционирования объекта (процесса), представленных в лингвистической форме в виде некоторой совокупности правил.

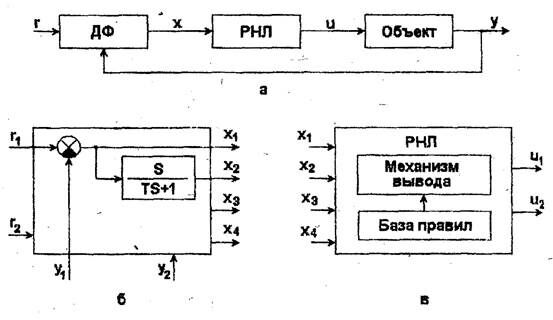
Рис. 5.1. Структурная схема системы нечеткого управления

На рис. 3.1 ДФ - динамический фильтр, выделяющий, помимо сигналов ошибок управления x₁=r₁-y₁ и х₃=r₂-у₂, производные от этих сигналов  и ;

РНЛ - регулятор на основе нечеткой логики ("нечеткий регулятор”, включающий в себя базу знаний (конкретнее - базу правил) и механизм логического вывода;

 -

соответственно векторы задающих воздействий (уставок), входов и выходов РНЛ, а также выходов объекта управления (т.е. парогенератора); т - операция транспонирования вектора.

В качестве входов и выходов РНЛ выступают:

 - отклонение давления в паровом котле (y₁) по отношению к и требуемому (номинальному) значению (r₁);

 - скорость изменения Р_Е;

 - отклонение скорости изменения давления (у₂) по отношению к его заданному значению (r₂);

 - скорость изменения SE;

u₁=H_c – изменение степени подогрева пара;

U₂=: Тс - изменение положения дросселя.

Мамдани предложил рассматривать эти величины как лингвистические переменные, каждая из которых может принимать одно из следующих значений из множества

                             L= {NB,NM,NS,NO,PO,PS,PM,PB}.                            

Здесь 1-я буква в обозначении указывает знак числовой переменной и соответствует английскому слову Negative ("отрицательное") или Positive ("положительное"), 2-я буква говорит об абсолютном значении переменной: Big ("большое"), Middle ("среднее"), Small ("малое") или О ("близкое к нулю"). Например, символ NS означает "отрицательное малое".

В процессе работы ИСУ в каждый момент времени используется один из двух нечетких алгоритмов: по первому из них осуществляется регулирование давления в котле путем изменения подогрева пара Н_c, по второму поддерживается требуемая скорость изменения давления с помощью изменения положения регулирующего дросселя Т_с. Каждый из алгоритмов состоит из ряда правил – высказываний, записанных на естественном языке, типа:

"Если отклонение давления в котле большое, отрицательного знака и если это отклонение не убывает с большой или средней по величине скоростью, то степень подогрева пара необходимо сильно увеличить".

Или:

"Если скорость изменения давления чуть ниже нормы и в то же время эта скорость резко растет, то следует изменить положение дросселя на положительную, достаточно малую, величину".

Используя введенные выше обозначения, можно переписать эти правила в следующем виде:

"ЕСЛИ (P_E=NB И C_PE=HE (NB ИЛИ NM), ТО Н_С=РВ";

"ЕСЛИ (S_E=NO И C_SE=PB), TO T_C=PS".

Реализация предложенных алгоритмов нечеткого управления при этом принципиально отличается от классических ("жестких") алгоритмов, построенных на основе концепции обратной связи (Feed-back Control) и, по существу, просто воспроизводящих некоторую заданную функциональную зависимость или дифференциальное уравнение.

Нечеткий регулятор берет на себя те функции, которые обычно выполняются опытным и умелым обслуживающим персоналом. Эти функции связаны с качественной оценкой поведения системы, анализом текущей меняющейся ситуации и выбором наиболее подходящего для данной ситуации способа управления объектом. Данная концепция управления получила название опережающего (или упреждающего) управления (Feed-Forward Control).

Используя образное сравнение, можно сказать, что примерно так действует опытный теннисист, каждый раз варьируя свой удар, чтобы мяч летел по определенной, выбранной им траектории, тогда как теннисный автомат работает по жестко заданной программе, подавая мяч всегда в одну и ту же точку, по одной и той же траектории.

Блок - схема нечеткого регулятора в общем случае принимает вид, изображенный на рис. 3.2.

Как видно из данной схемы, формирование управляющих воздействий u₁,u₂,...,u_m включает в себя следующие этапы:

а) получение отклонений управляемых координат и скоростей их изменения – х₁,x₂,...,х_n;

б) "фаззификация" этих данных, т.е. преобразование полученных значений к нечеткому виду, в форме лингвистических переменных;

в) определение нечетких (качественных) значений выходных переменных u₁,u₂,...,u_m (в виде функций их принадлежности соответствующим нечетким подмножествам) на основе заранее формулированных правил логического вывода, записанных в базе правил;

г) "дефаззификация", т.е. вычисление реальных числовых значений выходов u₁,u₂,...,u_m, используемых для управления объектом.

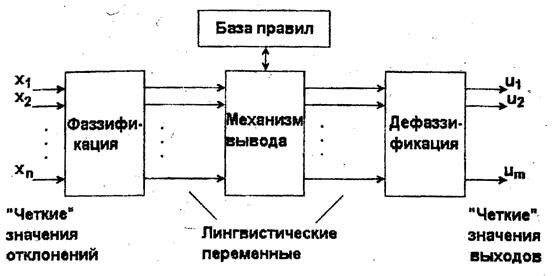
Рис. 3.2. Блок-схема нечеткого регулятора

Помимо представленного на рис. 3.1 варианта "чистого" использования нечеткого управления, существуют и другие варианты построения ИСУ с нечеткими регуляторами. Так, в классической теории регулирования широкое распространение получило использование ПИД - регулятора, выходной сигнал которого вычисляется по формуле

                                                            (3.1)

где параметры Кп, Ки и Кд характеризуют удельный вес соответственно пропорциональной, интегральной и дифференциальной составляющей и, должны выбираться исходя из заданных показателей качества регулирования (время регулирования, перерегулирование, затухание переходных процессов).

Возможное использование нечеткого регулятора (НР) для автоматической настройки (адаптации) указанных параметров ПИД - регулятора показано на рис. 3.3,а. Другие варианты применения HP – формирование уставок обычных регуляторов (рис. 3.3,6); подключение параллельно ПИД - регулятору (рис. 3.3, в); управление с предварительной оценкой характеристик сигналов (ОХС), получаемых с датчиков, на основе интерпретации их значимости, выделения обобщенных показателей качества и т. п. с последующей обработкой с помощью алгоритмов нечеткой логики (рис. 3.3,г).

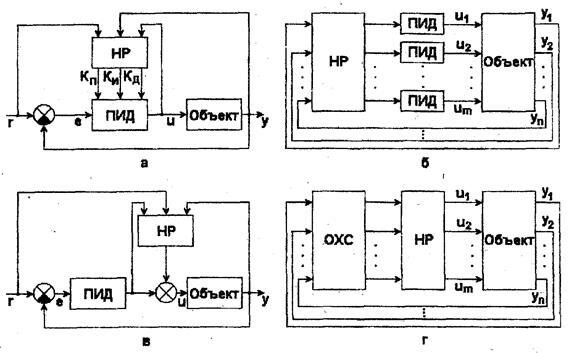
Рис. 3.3. Структуры ИСУ с нечеткими регуляторами

В качестве предпосылок к применению нечетких регуляторов обычно называются:

- большое число входных параметров, подлежащих анализу (оценке);

- большое число управляющих воздействий (многомерность);

- сильные возмущения;

- нелинейности;

Рекомендация для Вас - Биологические мембраны.

- неточности математических моделей программы регулирования;

- возможность использования технических знаний "know - how".

Подводя итог сказанному, отметим еще раз те области применения, в которых использование нечетких регуляторов оказывается более эффективным по сравнению с традиционными алгоритмами управления. Это:

1) приложения, которые пока были не связаны с автоматизацией, требующие применения "know - how", например, пивоварение (где можно воспользоваться знаниями экспертов с целью повышения качества продукции), подъемные краны (для повышения производительности рабочего персонала) и т. п.;

2) приложения, в которых математические методы не работоспособны. Это очень сложные процессы, не поддающиеся математическому описанию, для управления которыми можно использовать, наряду с эмпирическими знаниями, также полученную измерительную информацию (например, о ходе химических процессов);

3) приложения, в которых стандартные регуляторы достаточно хорошо работают; однако управление на основе нечеткой логики предлагает в данном случае альтернативный способ решения задач регулирования, возможность работы с лингвистическими переменными, более широкие возможности для оптимизации.