Для студентов ИДДО НИУ «МЭИ» по предмету Вычислительные методыИтоговый тестИтоговый тест
2024-01-292025-01-01СтудИзба
Ответы к экзамену: Итоговый тест
Описание
Итоговый тест сдан на оценку 5 . 100%
Вопросы из теста:
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у'= 5 у, у(0) = -3.2
Степень интерполяционного многочлена Лагранжа, который можно построить для табличной функции, заданной шестнадцатью значениями, равна.
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у'= exp(3ху),уy(0) = 0
Найти методом Ньютона с погрешностью, не превышающей О.01, корень уравнения f(x) = 0. 1/(x+ 1) -
Методом бисекции с заданной точностью е найти корень уравнения на заданном интервале. x + 2x-
Вычислить интеграл с шагом h по формуле трапеций![]()
![]()
![]()
![]()
![]()
![]()
Показать/скрыть дополнительное описание
Вопросы из теста:
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у'= 5 у, у(0) = -3.2
Степень интерполяционного многочлена Лагранжа, который можно построить для табличной функции, заданной шестнадцатью значениями, равна.
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у'= exp(3ху),уy(0) = 0
Найти методом Ньютона с погрешностью, не превышающей О.01, корень уравнения f(x) = 0. 1/(x+ 1) -
Методом бисекции с заданной точностью е найти корень уравнения на заданном интервале. x + 2x-
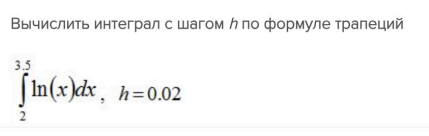
Вычислить интеграл с шагом h по формуле трапеций
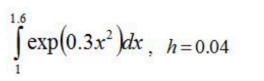
Показать/скрыть дополнительное описаниеИтоговый тест по вычислительным методам.
Характеристики ответов (шпаргалок) к экзамену
Предмет
Учебное заведение
ИДДО НИУ «МЭИ» Семестр
Теги
Просмотров
2
Качество
Идеальное компьютерное
Размер
935,99 Kb
Список файлов
вычислительные методы.pdf
Алёна Руденко
alena.rudenko.88
29 января 2024 в 17:07
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
