Для студентов ИДДО НИУ «МЭИ» по предмету Вычислительные методыИтоговый тестИтоговый тест
4,955196
2024-01-292025-01-01СтудИзба
Ответы к экзамену: Итоговый тест
Описание
Итоговый тест сдан на оценку 5. 100 %
Вопросы из теста:
Степень интерполяционного многочлена Лагранжа, который можно построить для табличной функции, заданной десятью значениями, равна:
Функция задана таблицей своих значений. Приблизить эту функцию многочленом второй степени. Среднеквадратичное отклонение в этом случае равно:
Методом бисекции с заданной точностью найти корень уравнения на заданном интервале. - - 5 = 0,
Определить как ведет себя метод простой итерации для линейной системы.
Указать количество верных цифр приближенного числа. a = 73.488931 Да = 0.01
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у' =
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у =
Найти методом Ньютона с погрешностью, не превышающей 0.01, корень уравнения f(x) 1/(5x + x) - x= 0.
Значения хи узаданы со всеми верными цифрами. Указать абсолютную погрешность для функции f(x, у). x= 0.236, y= 0.121, f(x, y)= 3x+ 2y
![]()
![]() Показать/скрыть дополнительное описание
Показать/скрыть дополнительное описание
Вопросы из теста:
Степень интерполяционного многочлена Лагранжа, который можно построить для табличной функции, заданной десятью значениями, равна:
Функция задана таблицей своих значений. Приблизить эту функцию многочленом второй степени. Среднеквадратичное отклонение в этом случае равно:
Методом бисекции с заданной точностью найти корень уравнения на заданном интервале. - - 5 = 0,
Определить как ведет себя метод простой итерации для линейной системы.
Указать количество верных цифр приближенного числа. a = 73.488931 Да = 0.01
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у' =
Дать ответ, как ведет себя модуль погрешности решения задачи Коши на отрезке [0, 10], если у =
Найти методом Ньютона с погрешностью, не превышающей 0.01, корень уравнения f(x) 1/(5x + x) - x= 0.
Значения хи узаданы со всеми верными цифрами. Указать абсолютную погрешность для функции f(x, у). x= 0.236, y= 0.121, f(x, y)= 3x+ 2y
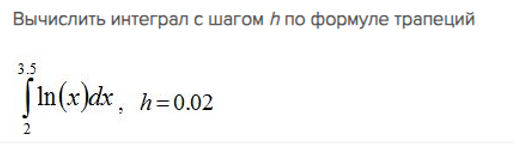
 Показать/скрыть дополнительное описание
Показать/скрыть дополнительное описаниеИтоговый тест.
Характеристики ответов (шпаргалок) к экзамену
Предмет
Учебное заведение
Семестр
Теги
Просмотров
5
Качество
Идеальное компьютерное
Размер
393,23 Kb
Список файлов
вычислительные методы Итоговый тест.docx
Алёна Руденко
Комментарии
Нет комментариев
Стань первым, кто что-нибудь напишет!
 ИДДО НИУ «МЭИ»
ИДДО НИУ «МЭИ»  alena.rudenko.88
alena.rudenko.88















