ztm5 (Р.М. Игнатищев, П.Н. Громыко, С.Н. Хатетовский - Курс теоретической механики - статика, кинематика, динамика)

Кривизна и радиус кривизны – арифметические величины.

Круг кривизны при точке траектории – это соприкасающийся с траекторией в её точке круг, радиус которого равен радиусу кривизны этой траектории в точке , а центр расположен на исходящей из точки главной нормали.

Центр кривизны траектории в точке - это центр круга кривизны при точке траектории.

Эволюта траектории - это геометрическое место центров кривизны траектории.

Замечание: у траектории, являющейся прямой линией, эволюта отсутствует (расположена в бесконечности от неё); если траекторией является окружность, то эволюта вырождается в точку (совпадающую с центром этой окружности).

Из дифференциальной геометрии известна так называемая

ф

17.21

ормула Френе - .

Выразим ускорение точки через рассмотренные понятия.-

.

Преобразовываем , учитывая формулу Френе:

.

Подставив полученное выражение в предыдущее, получаем

ф ормулы для определения ускорения точки при естественном способе задания её движения: , где

Положения касательной и нормальной составляющих ускорения

- касательная

и

17.22

- нормальная

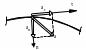
составляющие ускорения;

Рисунок 17.9

- касательное и - нормальное ускорения (в отличие от предыдущих терминов слово «составляющая» опущено).

Замечание: бинормальная составляющая ускорения всегда равна нулю.

97

Принято различать:

если , т.е. - движение равномерное;

если - движение переменное

(при - ускоренное; при - замедленное);

если - движение равнопеременное

(при - равноускоренное; при - равнозамедленное).

ПРИМЕР 17.1.- Определение скорости и ускорения по известным и

Дано. Движение точки вдоль траектории задано уравнением . Значения радиусов кривизны определяются уравнением , где - в см, - в секундах. Заданный момент времени

Определить модули скорости и ускорения движущейся точки в заданный момент времени .

Решение.- В соответствии с 17.16 проекция скорости точки на подвижную касательную (как функция времени): ;

в момент времени - см/с.

Координата (вдоль траектории) перемещающейся точки в момент времени : см.

Радиус кривизны траектории в той её точке, в которой в момент времени расположена движущаяся точка: см.

Для определения нормального ускорения используем результат 22: . В момент времени см/с².

Используя результат 17.22 определяем и касательное ускорение:

см/с² .

Модуль полного ускорения в момент времени :

см/с².

Замечание: при нижний индекс не поставлен потому, что касательное ускорение в рассматриваемом примере оказалось постоянной величиной; с целью

сокращения записей часто индекс не пишут и при .

98

П

К условию примера 2

РИМЕР 17.2.- Определение ускорения точки и закона её движения вдоль траектории

Д ано. Из точки по окружности радиуса м начинает двигаться точка . Проекция её ускорения на подвижную касательную изменяется по закону , где - в секундах, - в м/с². Через некоторый промежуток времени движущаяся точка оказалась расположенной в точке траектории с координатой м.

О

Рисунок 17.10

пределить закон движения точки вдоль траектории, т.е. , а также

промежуток времени и соответствующие ему скорость, нормальное, касательное и полное ускорения движущейся точки.

Решение.- В соответствии с 17.22,

.

находим из начальных условий (при ):

.

Таким образом, зависимость скорости от времени принимает вид: .

Т.к. , то

.

Принимаем, что при . Тогда: и уравнение движения точки вдоль траектории принимает вид: .

Учитывая, что при м, получаем:

.

Тогда:

99

м/с; м/с²; м/с²;

м/с².

Рекомендация:

ф ормулы, связывающие между собою скорости, ускорения, расстояния и моменты времени, зависят от конкретных исходных данных и могут быть различными; поэтому не следует загружать память частными математическими выражениями типа

(для рассмотренного примера они оказались непригодными);

ц

17.23

елесообразно в памяти хранить лишь зависимости и в совершенстве владеть методом интегрирования, а внутри его - процедурой определения постоянных и т.д.

Сделанный акцент на целесообразность свободного владения изложенным методом обусловлен не только задачами на кинематику точки при естественном способе задания движения; этот метод применяется в других разделах кинематики, в динамике, других дисциплинах - в сопротивлении материалов, электротехнике и т.д.

17.4. Подходы к определению кинематических величин, уравнений и радиусов кривизны траекторий при координатном способе описания движения точки

Радиус-вектор движущейся точки представляем тремя составляющими:

.

Его проекции ( ) равны, соответственно, абсциссе , ординате и аппликате движущейся точки, т.е.

.

Исходя из понятий о скорости и ускорении точки и учитывая постоянство ортов , получаем:

;

.

Откуда видно:

100

п

17.24

ри координатном способе задания движения точки проекции её скорости и ускорения определяются по формулам:

;

.

ПРИМЕР 17.3.- Определение скорости и ускорения точки при координатном способе задания движения

Дано. Движение точки задано уравнениями , ( и в см, - в секундах).

Определить модули скорости и ускорения движущейся точки в заданный момент времени .

Решение.-

.

В момент времени : см/с; направляющие косинусы - ;

; .

Аналогично для ускорения:

см/с²;

; ;

.

Уравнения движения точки - - по существу своему являются уравнениями траектории, но, говорят, в параметрической форме (через параметр ). Для получения уравнения траектории в координатной форме необходимо решить систему уравнений движения, исключив из них время , что рассмотрим на двух примерах.

ПРИМЕР 17.4.- Траектория точки. Полупрямая

Дано. Движение точки задано уравнениями , ( и в см, - в секундах).

Определить уравнение траектории точки в координатной форме

Рис10

101

Р

К примеру 17.4

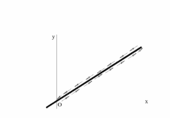ешение.- Т.к. , то точка расположена в плоскости . Из первого и второго уравнений: траектория точки расположена на прямой .

Замечание:

С

17.25

ледует различать траекторию и линию, на которой она расположена.

В

Рисунок 17.11

рассматриваемом примере траекторией является полупрямая, расположенная в первом квадранте (см. рис.17.11).

ПРИМЕР 17.5.- Траектория точки.. Пространственная линия

Дано.- Движение точки задано уравнениями:

,

Определить уравнение линии, на которой расположена траектория точки.

Решение.- Из 1-го и 3-го уравнений:

.

Из 1-го и 2-го уравнений:

.

Итак, в рассматриваемом примере траектория точки расположена на пространственной линии, описываемой системой уравнений:

ПРИМЕР 17.6.- Переход от координатного к естественному способу задания движения точки

Дано.- Движение точки задано уравнениями:

, .

( и в метрах, - в секундах).

Определить уравнение движения точки вдоль траектории, модули нормального и касательного ускорений.

102

Р

К примеру 17.6

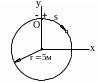ешение.- Возводя в квадраты и почленно складывая первые два уравнения, получаем:

,

т.е. траектория точки расположена в плоскости на окружности радиуса 5м (см. рис.17.12).

П

Рисунок 17.12

роекция скорости на подвижную касательную - это, с одной стороны, производная от координаты вдоль траектории, т.е. ; с другой стороны - взятый со знаком (+) или (-) модуль скорости, т.е.

.

За начало отсчёта для координаты принимаем точку окружности (в которой движущаяся точка находится в момент времени ). При таком условии .

За положительное направление отсчёта координаты вдоль траектории принимаем указанное на рис.17.12. Тогда:

м/с² .

ПРИМЕР 17.7.- Алгоритм определения радиусов кривизны траекторий при координатном способе задания движения точки

Дано. Движение точки задано уравнениями ( в метрах, - в секундах).

Определить радиус кривизны в той точке траектории, в которой в момент времени находится движущаяся точка.

Решение.- Проекции скорости и ускорения точки как функции времени:

Проекции скорости и ускорения точки в момент времени :

(скорости в м/с; ускорения в м/с²).

Т.к. , то .

103

Учитываем, что . Тогда: .

Итак, для момента времени получаем:

касательное ускорение - м/с²;

полное ускорение - м/с²;

нормальное ускорение - м/с²;

квадрат скорости - м²/с²;

радиус кривизны - м.

17.5*. Рекомендуемый подход к определению скоростей и ускорений точки при обобщённо-координатном способе описания её движения

Определяющие положение точки в пространстве (и изменяющиеся, поэтому, во времени) 3 независимые переменные в общем случае обозначаем

а

-

уравнения движения точки в обобщённых координатах.

Например, применительно к сферической системе (см. рис.3) можно обозначить: .

С целью определения скоростей и ускорений точки можно пойти по пути переведения описания её движения из обобщённых координат в декартовы.

Например, переход от описания движения точки в сферической системе координат к описанию движения этой же точки в декартовой системе осуществляется по формулам:

; ;

(вектор вначале разложен на и ; затем спроектирован на оси , а на ).

В общем случае получается:

б

( - первая, - вторая, - третья функции обобщённых координат).

Переход от (а) и (б) к проекциям скоростей ( ) и ускорений

104

( ) на оси декартовой системы координат осуществляется по правилам взятия производных от сложных функций. При этом, удобна следующая система обозначений:

«штрих» ( ) - символ частной производной (от соответствующих функций - );

нижний индекс («1 », «2 », «3 ») отображает переменную, по которой берётся частная производная (по ).