КМ-1. Введение в вычислительные системы. Внутрипроцессорный параллелизм. Расчетное задание. Сдано на оценку 5. Вариант 24

КМ-1. Введение в вычислительные системы. Внутрипроцессорный параллелизм. Расчетное задание. Сдано на оценку 5. Вариант 24

Сами здания:

Задание 1 Моделирование одноканальной СМО
Дано
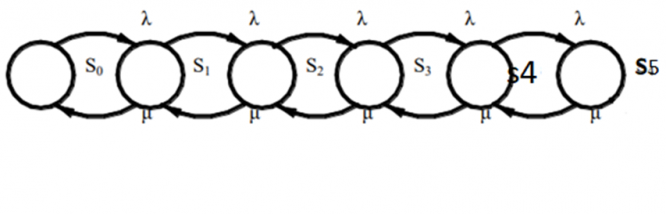
В системе с конечной очередью в каждый момент времени может быть одно из следующих состояний:
S0: в системе 0 заявок;
S1: в системе 1 заявка в канале обслуживания и 0 заявок в очереди;
S2: в системе 1 заявка в канале обслуживания и 1 заявок в очереди;
S3: в системе 1 заявка в канале обслуживания и 2 заявок в очереди;
S4: в системе 1 заявка в канале обслуживания и 3 заявок в очереди;
S5: в системе 1 заявка в канале обслуживания и 4 заявок в очереди;

Система может находиться в одном из состояний S0, S1, S2, …, Sk, по числу заявок, находящихся в СМО: S0 — канал свободен; S1 — канал занят (обслуживает заявку), очереди нет, S2 — канал занят, одна заявка стоит в очереди; ... Sk — канал занят, (k—1) заявок стоят в очереди и т.д.
Контрольные вопросы.
1. Дайте определение Марковского процесса с дискретным временем.
2. Составьте матрицу переходных вероятностей размерности 4 Х 4 для Марковского процесса с дискретным временем. Численные значения переходных вероятностей определите самостоятельно.
3. Каким свойством обладает сумма переходных вероятностей, записанных в
строках матрицы переходных вероятностей?
4. Каков математический (физический) смысл этого свойства с точки зрения
теории вероятностей?
5. Нарисуйте граф переходов для составленной в п. 2 матрицы переходных
вероятностей.
6. Дайте определение Марковского процесса с непрерывным временем.
7. Составьте матрицу переходных интенсивностей размерности 4 Х 4 для
Марковского процесса с непрерывным временем. Численные значения переходных
интенсивностей определите самостоятельно.
8. Каковы размерности вероятности и интенсивности потока событий?
9. Нарисуйте граф переходов для Марковского процесса с матрицей интенсивностей,
составленной в п. 7.
10. Нарисуйте структурную схему одноканальной СМО с очередью.
11. Составьте список состояний СМО, имеющей один канал обслуживания и три места в очереди.
12. Нарисуйте граф переходов для СМО, имеющей один канал обслуживания и три места в очереди.
13. Запишите систему дифференциальных уравнений Колмогорова для этой
СМО.
14. Задайте и поясните смысл начальных условий для этой системы.
15. Разберите понятия переходного и стационарного режимов работы СМО.
16. Запишите вариант стационарной системы уравнений Колмогорова для этой
СМО. Какое условие заменяет начальные условия в стационарной системе. Какой
смысл имеет это условие с точки зрения теории вероятности.
17. Решите стационарную систему Колмогорова для этой СМО.
18. Рассчитайте основные характеристики СМО.
19. Проведите численный расчет этого варианта СМО по одной из программПоказать/скрыть дополнительное описание