Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

Министерство образования Республики Беларусь

Учреждение образования

"Гомельский государственный университет им. Ф. Скорины"

Математический факультет

Кафедра МПМ

Изучение тригонометрического материала в школьном курсе математики

Реферат

Исполнитель:

Студентка группы М-42 Головачева А.Ю.

Научный руководитель:

Канд. физ-мат. наук, доцент Лебедева М.Т.

Гомель 2007

Содержание

Введение

1. Методика введения понятий синуса, косинуса и тангенса на геометрическом материале. Основные тригонометрические тождества

2. Методика введения определений тригонометрических функций углов от 0° до 180°

3. Методика изучения тригонометрических функций в курсе алгебры

4. Тождественные преобразования тригонометрических выражений. Тригонометрические уравнения и неравенства и методика обучения решению

Заключение

Литература

Введение

Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 0⁰ до 180⁰; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.

Первые два этапа реализуются в курсе планиметрии. Геометрический характер определений тригонометрических функций объясняет тот факт, что они составляют единственный вид функций, который начинают изучать не в курсе алгебры, а в курсе геометрии. Для геометрии важен "общефункциональный взгляд" на тригонометрические функции, а их прикладная сторона (решение прямоугольных треугольников, применение некоторых тригонометрических тождеств, теорем cos и sin, решение произвольных треугольников). Поэтому в курсе планиметрии нет термина "тригонометрические функции".

1. Методика введения понятий синуса, косинуса и тангенса на геометрическом материале. Основные тригонометрические тождества

Знакомство с тригонометрическим материалом начинается в курсе геометрии при знакомстве с прямоугольным треугольником. Понятия , и острых углов треугольника вводится для углов от до , как отношение сторон этого треугольника. Предварительно учащиеся должны усвоить названия сторон прямоугольного треугольника: катеты (стороны прямого угла) и гипотенуза (сторона противолежащая прямому углу). Для этого необходимо предложить учащимся прямоугольные треугольники, разнообразные по расположению вершин прямого угла и предложить назвать стороны треугольника.

Назовите катеты в ABC, APN. Назовите гипотенузы в LKM и EFA. Будут ли гипотенузами следующие отрезки: AB, KL, AP, AN, EF, FA в указанных треугольниках и почему?

Следующие выражения "прилежащий" и "противолежащий" отрабатываются на следующем этапе. Для этого необходимо по указанным треугольникам предложить учащимся назвать прилежащие и противолежащие острым углам катеты. Назвать отрезки: KL, PN, EA и попросить учащихся назвать те углы, против которых лежат эти катеты или, которым они прилегают.

Первым вводится понятие угла и доказывается теорема: " Косинус угла зависит от градусной меры угла и не зависит от расположения и размеров треугольника". Это определение уже " работает" при доказательстве теоремы Пифагора.

С остальными понятиями учащиеся знакомятся в пункте " Соотношения между сторонами и углами в прямоугольном треугольнике". sin , tg

Формируется свойство: синус и тангенс угла так же, как и косинус, зависят от величины угла.

Для синуса это доказывается так:

= ,

так как косинус зависит только от величины угла, то и синус зависит только от величины угла.

Из определений , и получаем следующие правила:

• Катет, противолежащий углу , равен произведению гипотенузы на синус ;

• Катет, прилежащий к углу , равен произведению гипотенузы на косинус ;

• Катет, противолежащий углу , равен произведению второго катета на тангенс .

По этим правилам можно находить неизвестные элементы в прямоугольном треугольнике.

Перечисленные правила могут быть выведены учащимися самостоятельно. Для этого предлагаются вопросы: В прямоугольном треугольнике MNP, LN= , LM= , гипотенуза MP=m. Найти длины катетов этого треугольника. ( Задача решается по определению).

Раньше по программе тригонометрические функции и соотношения между углами и сторонами в прямоугольном треугольнике изучались в курсе 8 класса.

После введения понятий , и рассматривались решения основных задач, связанных с отысканием длин сторон и величин углов в прямоугольном треугольнике.

Задача №1. Дано: a, b. Требуется найти A, B, c.

Задача №2. Дано: a, c. Требуется найти A, B, b.

Задача №3. Дано: a, A. Требуется найти A, b, c.

Задача №4. Дано: a, B. Требуется найти A, b, c.

Задача №5. Дано: a, A. Требуется найти B, a, b.

По действующей программе эти задачи в курсе 8 класса (бывший 7 класс) заменены такой: В прямоугольном треугольнике даны: гипотенуза c и острый угол . Найдите катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу.

Вводятся основные тригонометрические тождества:

, , , .

В частности, основное тригонометрическое тождество выводится из формулировки теоремы Пифагора:

, .

Учащиеся знакомятся с некоторыми свойствами функций острого угла: 1) при возрастании острого угла и возрастают, а - убывает; 2) для любого острого угла : , ; которые формулируются как теоремы. Их доказательство связывается с соотношениями острых углов в прямоугольном треугольнике:

, , тогда , .

,

тогда из равенства правых частей получаем:

.

, тогда .

Вывод свойства возрастания и убывания выглядит так:

Пусть и - острые углы, и , и она пересекает стороны углов и в точках и соответственно.

Так как , то точка лежит между точками и , тогда . А значит, по свойству наклонных, (через сравнение их проекций). Так как , , то косинус убывает. А так как , то синус возрастает.

2. Методика введения определений тригонометрических функций углов от до

Расширение области определения тригонометрических функций от до происходит в теме: "Декартовы координаты на плоскости".

Рассмотрим окружность с центром в начале координат произвольного радиуса R. Откладываем в полуплоскость угол . Пусть точка имеет координаты и . , , то из треугольника : , .

Определяются значения и этими формулами для любого угла α (для ⁰-исключается).

Можно найти значения этих функций для углов 90⁰, 0⁰, 180⁰. Доказывается, что для любого угла α , 0⁰<α<180⁰, .

п

y

овернем подвижный радиус на угол 180⁰-α=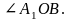

А₁(x₁, y₁)

180⁰-α

по гипотенузе и острому углу: => OB₁=OB; A₁B₁=AB => x = -x₁,y = y₁=>

B₁

α

R

O

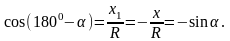
Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности.

Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 0⁰ до 180⁰; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.

Первые два этапа реализуются в курсе планиметрии. Геометрический характер определений тригонометрических функций объясняет тот факт, что они составляют единственный вид функций, который начинают изучать не в курсе алгебры, а в курсе геометрии. Для геометрии важен "общефункциональный взгляд" на тригонометрические функции, а их прикладная сторона (решение прямоугольных треугольников, применение некоторых тригонометрических тождеств, теорем cos и sin, решение произвольных треугольников). Поэтому в курсе планиметрии нет термина "тригонометрические функции".

Конкретизировать, например, понятие cos острого угла прямоугольного треугольника, можно по следующей методической схеме:

1. построить на миллиметровой бумаге прямоугольный треугольник ABC;

2. обозначить величину острого угла А буквой α;

3. измерить (по клеткам) прилежащий катет АС и гипотенузу АВ;

4. вычислить отношение

5. записать значение cos α (делается следующая запись cos α ≈ в которой для α не указывается его конкретное значение);

6. измерить транспортиром угол α, найти его величину и записать значение косинуса этого угла данного прямоугольного треугольника.

Определенные трудности в изучение элементов тригонометрии (по Пифагору) порождает теорема: "Косинус угла α зависит только от градусной меры угла". Необходимость изучения данной теоремы можно разъяснить учащемуся так: Пусть требуется на основании определения найти cos 37⁰. Предположим, что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 37⁰, они построят прямоугольный треугольник (каждый свой) с углом в 37⁰, измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 37⁰. Есть ли гарантия, что каждый ученик получит один и тот же ответ? Этот вопрос возникает по той причине, что каждый строит свой треугольник, получает свои значения длин прилежащего катета и гипотенузы. Так, может быть, и искомое отношение у каждого ученика будет какое-то свое? Понятно, что если бы значение cos 37⁰ при переходе от одного прямоугольного треугольника к другому изменялось, то ценность такого понятия в математике была бы не велика. Изучаемая терема является ответом на поставленные вопросы. Она утверждает, что косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов реферата