115364 (711654), страница 2
Текст из файла (страница 2)
При решении прямоугольных треугольников необходимо обратить внимание учащегося на тот факт, что с каждой из формул для cos, sin и tg α связывается еще две формулы:









Определение cos, sin, tg углов от 00 до 1800 являются генетическими, т.к. в них указываются построения и вычисления, позволяющие найти значение тригонометрической функции.
В пособие говорится следующее (стр. 132, 1, 2 абзац), обратите внимание учащихся на следующее обстоятельство. Ранее для острых углов были установлены некоторые тригонометрические тождества. "Справедливы ли эти тождества для углов от 00 до 1800. Справедливы ли прежние доказательства этих тождеств или необходимо привести новые?"
Сравним доказательства основного тригонометрического тождества:  для острых углов и для углов от 00 до 1800:
для острых углов и для углов от 00 до 1800:
| 00<α<900 | 00≤α≤1800 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
В курсе "Алгебра 9" обобщается определение cos, tg и sin α на случай произвольного угла α и вводится понятие ctg α. Возможность такого обобщения – во введении понятия угла поворота, положительного и отрицательного угла, понятия полного оборота. Доказывается, что тригонометрические функции, их значение, не зависит от длины радиуса.
Здесь же приведены с доказательствами основные тригонометрические формулы, формулы сложения и их следствия.
3. Методика изучения тригонометрических функций в курсе алгебры
Традиционная методическая схема изучения тригонометрических функций:
-
в начале определяются тригонометрические функции для острого угла прямоугольного треугольника;
-
затем введенные понятия обобщаются для углов от
![]() до
до ![]() ;
; -
тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
В курсе алгебры и начала анализа осуществляется заключительный этап изучения, который включает:
-
Закрепление представлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот;
-
Формирование представлений об углах с градусной мерой, большей
![]() ; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа);
; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа); -
Описание тригонометрических функций на языке радианной меры угла;
-
Утверждение функциональной точки зрения на
![]() ,
, ![]() , и
, и ![]() (трактовка
(трактовка ![]() ,
, ![]() , и
, и ![]() как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т.д.);
как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т.д.); -
Повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом которых является тождество
![]() ;
; -
Применение тригонометрических тождеств в тождественных преобразованиях и при решении задач по стереометрии.
В курсе "Алгебра 9" учащиеся знакомятся с функциональной точкой зрения. Выражения  и
и  определимы при
определимы при  , т.к
, т.к  угла поворота можно найти соответствующее значение дробей
угла поворота можно найти соответствующее значение дробей  и
и  . Выражение
. Выражение  имеет смысл при
имеет смысл при  , кроме углов поворота
, кроме углов поворота  ,
,  , …, т.к. имеет смысл дробь
, …, т.к. имеет смысл дробь  .
.
Каждому допустимому значению  соответствует единственное значение
соответствует единственное значение  ,
,  ,
,  и
и 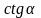 . Поэтому
. Поэтому  ,
,  ,
,  и
и  являются функциями угла
являются функциями угла  . Их называют тригонометрическими функциями.
. Их называют тригонометрическими функциями.
Учащиеся знакомятся со следующими общефункциональными свойствами этих функций:
-
область значения
![]() и
и ![]() -
- ![]() , для
, для ![]() и
и ![]() - множество всех действительных чисел
- множество всех действительных чисел -
промежутки знакопостоянства:
![]() , то значит
, то значит ![]() зависит от знака
зависит от знака ![]() и т.д.
и т.д. -
![]() ,
, ![]() и
и ![]() являются нечетными функциями, а
являются нечетными функциями, а ![]() является четной функцией
является четной функцией -
при изменении угла на целое число оборотов значение
![]() ,
, ![]() ,
, ![]() ,
, ![]() не изменится (под обратным понимаем поворот на
не изменится (под обратным понимаем поворот на ![]() ).
).
Введение радианной меры угла основывается на том факте, что отношения длины окружности к её радиусу постоянно для данного центрального угла и не зависит от выбора концентрических окружностей. По этой причине меру центрального угла можно охарактеризовать действительным числом  . Если
. Если  положить равным 1, то радианная мера центрального угла равна 1, т.е.
положить равным 1, то радианная мера центрального угла равна 1, т.е.  .
.
Тогда для каждого угла, заданного в градусах, достаточно вычислить соответствующую дугу единичной окружности. Длина такой дуги будет выражать меру данного угла в радианах.
Радианная мера угла позволяет любому действительному числу поставить в соответствие определенную градусную меру угла по формуле:  , где
, где  .
.
Переход от радианной меры угла к действительному числу осуществляется на основании того, что  . Учащимся следует показать изменение величин углов по координатным углам:
. Учащимся следует показать изменение величин углов по координатным углам:
1 четверть:  ,
,  ;
; 
2 четверть:  ,
,  ;
;  и т.д.
и т.д.
Определение тригонометрической функции  выглядит так:
выглядит так:
Опр. Окружность радиуса 1 с центром в начале координат называют единичной
окружностью. Пусть точка  единичной окружности получена при повороте точки
единичной окружности получена при повороте точки  на угол в
на угол в  радиан. Ордината точки
радиан. Ордината точки  - это синус угла
- это синус угла  . Числовая
. Числовая  функция, заданная формулой
функция, заданная формулой  , называется синусом числа, каждому числу
, называется синусом числа, каждому числу  ставится в соответствие число
ставится в соответствие число  .
.
Устанавливаются области определения и значения функций, напоминаются свойства:
 ;
;  .
.
Построим график функции ![]() на
на ![]() .
.
Делим единичную окружность и отрезок ![]() на 16 равных частей.
на 16 равных частей.
Через точку  проводим прямую, параллельную
проводим прямую, параллельную  . Проводим прямую
. Проводим прямую  до пересечения с построенной прямой. Получим одну из точек графика функции
до пересечения с построенной прямой. Получим одну из точек графика функции  , называемого синусоидой.
, называемого синусоидой.
Отрезок оси ![]()
![]() , с помощью которого находятся значения синуса, называется линией синусов.
, с помощью которого находятся значения синуса, называется линией синусов.
Для построения графика синуса вне этого отрезка заметим, что  . Поэтому во всех точках вида
. Поэтому во всех точках вида  , где
, где  , значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси
, значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси  .
.
Для построения графика косинуса следует вспомнить, что  . Следовательно, значение косинуса в произвольной точке
. Следовательно, значение косинуса в произвольной точке  равно значению синуса в точке
равно значению синуса в точке  . Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние
. Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние  в отрицательном направлении оси
в отрицательном направлении оси  . Поэтому график функции
. Поэтому график функции  также является синусоидой.
также является синусоидой.
Для функций ![]() и
и ![]() определяется аналогично. Область определения
определяется аналогично. Область определения ![]() - множество всех чисел, где
- множество всех чисел, где ![]() .
.
Построение графика: проведем касательную  к единичной окружности в точке
к единичной окружности в точке  .
.

Пусть  произвольное число, для которого
произвольное число, для которого  . Тогда точка
. Тогда точка  не лежит на оси ординат, и, следовательно, прямая
не лежит на оси ординат, и, следовательно, прямая  пересекает
пересекает  в некоторой точке
в некоторой точке  с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая
с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая  проходит через точки
проходит через точки  и
и  . Поэтому она имеет уравнение
. Поэтому она имеет уравнение  .
.
Абсцисса точки  , лежащей на этой прямой, равна 1. Из уравнения прямой
, лежащей на этой прямой, равна 1. Из уравнения прямой 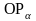 находим, что ордината точки
находим, что ордината точки  равна
равна  . Итак, ордината точки пересечения прямых
. Итак, ордината точки пересечения прямых 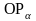 и
и  равна
равна  . Поэтому прямую
. Поэтому прямую  называют линией тангенсов.
называют линией тангенсов.
Н







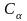 пересечения прямой
пересечения прямой 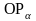 с касательной m к единичной окружности, проведённой через точку
с касательной m к единичной окружности, проведённой через точку 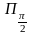 , равна
, равна 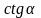 при
при 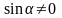 .
.Поэтому прямую m называют линией котангенсов.
Область значений ![]() - вся числовая прямая. Докажем это для функции
- вся числовая прямая. Докажем это для функции ![]() . Пусть
. Пусть ![]() - произвольное действительное число. Рассмотрим точку
- произвольное действительное число. Рассмотрим точку ![]() . Как только что было показано,
. Как только что было показано, ![]() равен
равен ![]() . Следовательно, функция
. Следовательно, функция ![]() принимает любое действительное значение
принимает любое действительное значение ![]() , ч.т.д.
, ч.т.д.
Построение графика аналогично построению ![]() .
.
Можно построить схему, позволяющую изобразить график тригонометрических функций:
-
Начертить единичную окружность, горизонтальный диаметр которой служит продолжением оси
![]() . Разделить её на равные части (например,16).
. Разделить её на равные части (например,16). -
Для функции
![]() выбираем отрезок
выбираем отрезок ![]() , для функции
, для функции ![]() -
- ![]() и делим их на то же равное число частей.
и делим их на то же равное число частей. -
По окружности находим соответствующее число значений этих функций.
-
Точки пересечения горизонтальных линий, отвечающих значениям функций и вертикальных линий, отвечающих значениям аргумента, представляют собой точки графика.
4. Тождественные преобразования тригонометрических выражений. Тригонометрические уравнения и неравенства и методика обучения решению
Тригонометрический материал изучается в школьном курсе в несколько этапов.
-
Функции тригонометрических функций для углов от
![]() до
до ![]()
(прямоугольный треугольник, планиметрия);
-
Тригонометрические функции для углов от
![]() до
до ![]() (тема: "Декартовы координаты на плоскости; геометрия");
(тема: "Декартовы координаты на плоскости; геометрия"); -
Тригонометрические функции для любого действительного числа.
Параллельно изучению теоретического материала учащиеся знакомятся с тригонометрическими формулами, объём которых будет постепенно рассширяться. Умение "выделить" эти формулы в дальнейшем поможет в преобразовании тригонометрических выражений.
К обязательным результатам обучения за курс геометрии в 7-9 классах относиться умение решать типичные задачи на вычисление значений геометрических величин (длин, углов, площадей) с привлечением свойств фигур, аппарата алгебры и тригонометрии.
Например:
-
В прямоугольном треугольнике найдите катеты, если его гипотенуза равна 5 см, а один из углов равен
![]() .
. -
В прямоугольном треугольнике катет равен 4 см, а прилежащий к нему угол равен
![]() . Найдите другой катет и гипотенузу.
. Найдите другой катет и гипотенузу. -
В
![]()
треугольнике ABC: AB=3см, BC=6 см,![]()
![]() . Определите
. Определите ![]() .
. -
В треугольнике ABC известны стороны: AB=4 см; BC=5 см; AC=6 см.
Н

Существуют различные доказательства формулы косинуса суммы двух аргументов.
О

-
![]() ;
; -
![]() ;
; -
![]() ;
; -
![]() ;
; -
![]() .
. -
![]() ;
;
 , ч.т.д.
, ч.т.д.
 ;
; 
 .
.
С





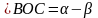
 - теорема сложения.
- теорема сложения.

и по доказанной формуле.
Для доказательства  суммы и разности двух углов используются формула приведения, которые помогают преобразовать функции от аргументов вида:
суммы и разности двух углов используются формула приведения, которые помогают преобразовать функции от аргументов вида:

 ,
,  ,
,  ,
,  .
.
Проведём радиус  , длина которого равна
, длина которого равна  , на угол
, на угол  : и получили радиус
: и получили радиус  , где
, где  и на угол
и на угол  и получим радиус
и получим радиус  , где
, где  .
.
 ,
,  :
:  ,
,  .
.
 - прямоугольник. Повернём его на угол
- прямоугольник. Повернём его на угол  вокруг точки
вокруг точки  :
:
 ;
;  ;
;  , т.е.
, т.е.
 ;
;  , т.е:
, т.е:
 ;
;  , по
, по 

Аналогично:


Тогда:



и т.д.

К функциям от углов  можно прийти и из геометрических соображений.
можно прийти и из геометрических соображений.
Формулы приведения для  и
и  выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере:
выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере:
 {определяем четность, в которой оканчивается угол
{определяем четность, в которой оканчивается угол  - II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:}
- II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:}  = - cos
= - cos  .
.
Вернёмся к выводу формулы синуса суммы и разности двух углов.
 ,
,
а затем применяется уже известная формула.
Формулы двойного угла выводятся из формулы синуса и косинуса суммы и разности двух углов, положив  .
.
Сумму и разность тригонометрических функций можно преобразовать в произведение, используя следующий пример:
 ={
={  ,
,  }=
}=
= ,
,
но:

Таким образом:

Замечание: при ознакомлении учащихся с формулами следует добиваться от них проговаривания словесных формулировок доказываемых формул.
Например: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
В курсе алгебры 9 класса изучается тема: "Элементы тригонометрии" (30 часов):
1) радианное измерение углов, sin, cos, tg произвольного угла, их нахождение с помощью калькулятора;
2) основные тригонометрические тождества:

Их применение для вычисления значений sin, cos, tg;
3) формулы приведения; sin, cos суммы и разности двух углов; sin и cos двойного угла;
4) тождественные преобразования тригонометрических выражений; основная цель – сформировать умения выполнять тождественные преобразования несложных тригонометрических выражений с использованием формул, указанных в программе:
Рассмотрим некоторые примеры преобразований тригонометрических выражений:
Задача №1.
Доказать тождество:

Преобразуем левую часть и получим, применив формулы приведения:
 8
8 cos4
cos4 +sin8
+sin8 =2sin8
=2sin8 cos4
cos4 +2sin4
+2sin4 cos4
cos4 =2cos4
=2cos4 (sin8
(sin8 +sin4
+sin4 )=4cos4
)=4cos4 sin6
sin6 cos2
cos2 , и т.д.
, и т.д.
Задачи №2.
Упростить выражение
а) 
Можно применить формулы понижения степени:
 =
=
 {воспользуемся преобразованием разности косинусов в произведение по формуле:
{воспользуемся преобразованием разности косинусов в произведение по формуле:  } =
} =

б)

Задача №3
Преобразовать в произведение:
а) cos5 +sin8
+sin8 +cos9
+cos9 +cos12
+cos12 =(cos5
=(cos5 +cos12
+cos12 )+(cos8
)+(cos8 +cos9
+cos9 )=
)=
=2cos17/2 cos7/2
cos7/2 +2cos17/2
+2cos17/2 cos
cos /2=2cos17/2
/2=2cos17/2 (cos7/2
(cos7/2 +cos
+cos /2)=
/2)=
=4cos17/2 cos2
cos2 cos3/2
cos3/2 =4cos3/2
=4cos3/2 cos2
cos2 cos17/2
cos17/2
б) 3+4cos4 +cos8
+cos8 =3(1+cos4
=3(1+cos4 )+(cos4
)+(cos4 +cos8
+cos8 )=6cos22
)=6cos22 +
+
+2cos6 cos2
cos2 =2 cos2
=2 cos2 (3cos2
(3cos2 +cos6
+cos6 )=2cos2
)=2cos2 ((cos2
((cos2 +|cos6
+|cos6 )+
)+
+2cos2 )=2cos2
)=2cos2 (2cos4
(2cos4 cos2
cos2 +2cos2
+2cos2 )=4cos22
)=4cos22 (cos4
(cos4 +cos2
+cos2 )=
)=
=4cos22 cos22
cos22 =8cos42
=8cos42
Задача №4
Найти sin4 +cos4
+cos4 , если известно, что:
, если известно, что:
sin -cos
-cos =1/2
=1/2
sin4 +cos4
+cos4 =(sin2
=(sin2  +cos2
+cos2 )2-2sin2
)2-2sin2 cos2
cos2 =1-2sin2
=1-2sin2 cos2
cos2 =
=
=1-1/2sin22 ={sin4
={sin4 -cos
-cos =1/2
=1/2 (sin
(sin -cos
-cos )2=
)2=
=1-2sin cos
cos =1/4
=1/4 sin2
sin2 =3/4}=
=3/4}=
Задача №5
Вычислить:

sin =-cos(2arctg4/3)={обозначим arctg4/3 через y, тогда получим cos2y, который нужно преобразовать в тангенс половинного угла. Применим формулу
=-cos(2arctg4/3)={обозначим arctg4/3 через y, тогда получим cos2y, который нужно преобразовать в тангенс половинного угла. Применим формулу  и получим}=
и получим}= 
Заключение
Определенные трудности в изучение элементов тригонометрии (по Пифагору) порождает теорема: "Косинус угла α зависит только от градусной меры угла". Необходимость изучения данной теоремы можно разъяснить учащемуся так: Пусть требуется на основании определения найти cos 370. Предположим, что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 370, они построят прямоугольный треугольник (каждый свой) с углом в 370, измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 370. Есть ли гарантия, что каждый ученик получит один и тот же ответ? Этот вопрос возникает по той причине, что каждый строит свой треугольник, получает свои значения длин прилежащего катета и гипотенузы. Так, может быть, и искомое отношение у каждого ученика будет какое-то свое? Понятно, что если бы значение cos 370 при переходе от одного прямоугольного треугольника к другому изменялось, то ценность такого понятия в математике была бы не велика. Изучаемая терема является ответом на поставленные вопросы. Она утверждает, что косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.
Литература
1. К.О. Ананченко "Общая методика преподавания математики в школе", Мн., "Унiверсiтэцкае",1997г.
2.Н.М.Рогановский "Методика преподавания в средней школе", Мн., "Высшая школа", 1990г.
3.Г.Фройденталь "Математика как педагогическая задача",М., "Просвещение", 1998г.
4.Н.Н. "Математическая лаборатория", М., "Просвещение", 1997г.
5.Ю.М.Колягин "Методика преподавания математики в средней школе", М., "Просвещение", 1999г.
6.А.А.Столяр "Логические проблемы преподавания математики", Мн., "Высшая школа", 2000г.
 до
до  ;
; ; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа);
; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа); ;
; , для
, для  , то значит
, то значит  .
.


 - вся числовая прямая. Докажем это для функции
- вся числовая прямая. Докажем это для функции  - произвольное действительное число. Рассмотрим точку
- произвольное действительное число. Рассмотрим точку  . Как только что было показано,
. Как только что было показано,  . Разделить её на равные части (например,16).
. Разделить её на равные части (например,16). , для функции
, для функции  и делим их на то же равное число частей.
и делим их на то же равное число частей. до
до 
 (тема: "Декартовы координаты на плоскости; геометрия");
(тема: "Декартовы координаты на плоскости; геометрия"); .
. . Найдите другой катет и гипотенузу.
. Найдите другой катет и гипотенузу.
 . Определите
. Определите  .
. 
 ;
; ;
; ;
; ;
; .
. ;
;
















