Kompleksni_chisla (675849), страница 3

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

(6 + 5i) – (3 + 8i) = 3 – 3i;

(5 – 4i)(8 – 9i) = 4 – 77i;

.

Свойства действий

над комплексными числами

Для любых комплексных чисел α = a + bi, β = с + di, γ = e + fi выполняются следую­щие свойства действий сложения и умножения:

1) α + β = β + α – переместительное (коммутатив­ное) свойство сложения;

2) (α + β) + γ = α + (β + γ) – сочетательное (ассоциативное) свойство сложения;

3) αβ = βα – переместительное (комму­тативное) свойство умножения;

4) (αβ)γ = α(βγ) – сочетательное (ассоциативное) свойство умножения;

5) (α + β)γ = αγ + βγ – распределительное (дистри­бутивное) свойство умножения относительно сло­жения.

Докажем, например, первое и третье из этих свойств. По определению сложения получаем

α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,

β + α = (c + di) + (a + bi) = (c + a) + (d + b)i = (a + c) + (b + d)i = α + β,

так как с + a = a + с, d + b = b + d, т. е. для любых действительных чисел выполняется переместительное (коммутативное) свойство сложения. Далее,

αβ = (a + bi)(c + di) = aс + adi + bci + bdi² = (ac - bd) + (ad + bc)i,

βα = (c + di) (a + bi) = сa + cbi + dai + dbi² = (ca - db) + (cb + da)i = (ac - bd) + (ad + bc)i = αβ,

поскольку для любых действительных чисел ac = ca, bd = db, т. е. выполняется перемести­тельное (коммутативное) свойство умножения.

Остальные свойства доказываются аналогично, с учетом соответствующих свойств операций над дей­ствительными числами.

Таким образом, операции над комплексными числами подчиняются тем же законам, что и опера­ции над действительными числами.

Возведение в степень комплексного числа.

Извлечение корня из комплексного числа

При возведении в степень комплексного числа пользуются формулой бинома Ньютона:

.

С помощью формулы бинома Ньютона получаем

.

В правой части этого равенства заменяют сте­пени мнимой единицы i их значениями и приводят подобные члены. Рассмотрим, как выражаются эти степени. Учитывая формулу i² = - 1 , получаем i³ = i² ∙ i = -1 ∙ i = - i, i⁴ = i³ ∙ i = -i ∙ i = -i² = 1, i⁵ = i⁴ ∙ i = i, i⁶ = i⁵ ∙ i = i² = -1, i⁷ = i⁶ ∙ i = -i, i⁸ = i⁷ ∙i = - i² = 1 и т. д. В общем виде полученный результат можно записать так:

i^4k = 1, i^4k+1 = i, i^4k+2 = -1, i^4k+3 = - i (k = 0, 1, 2, …).

Например: (3 + 4i)² = 3² + 2 ∙ 3 ∙ 4i + (4i)² = 9 + 24i + 16i² = 9 + 24i – 16 = -7 + 24i;

(1 + i)³ = 1 + 3i + 3i² + i³ = 1 + 3i – 3 – i = - 2 + 2i.

Переходим к извлечению квадратного корни из комплексного числа a + bi. Квадратным корнем из комплексного числа называют такое комплексное число, квадрат которого равен данному комплексно­му числу. Обозначим это комплексное число через u + vi, т. е.

.

Последнее равенство перепишем в следующем виде:

u² + 2uvi + v²i² = a + bi, u² – v² + 2uvi = a + bi.

Учитывая определение равенства комплексных чисел (см. (10)), получаем

u² – v² = a, 2uv = b. (15)

Возведем в квадрат обе части каждого из этих равенств, сложим их, преобразуем полученную левую часть и извлечем квадратный корень:

(u² – v²)² + 4u²v² = a² + b², (u² + v²)² = a² + b², u² + v² = .

Это уравнение и первое из уравнений (15) дают возможность определить u² и v² :

. (16)

Из первого уравнения находим два значения u, отличающиеся друг от друга только знаком, второе уравнение дает два значения v. Все эти значения будут действительными, поскольку при любых a и b

.

Знаки u и v следует выбирать так, чтобы выполнялось второе из равенств (15). Это дает две возможные комбинации значений u и v, т. е. два числа u₁ + v₁i, u₂ + v₂i, отличающиеся знаком.

Следовательно, извлечение квадратного корня из комплексного числа всегда возможно и дает два значения, отличающиеся друг от друга только знаком.

Например: пусть требуется извлечь квадратный корень из комплексного числа 3 — 4i, т. е. найти комплексное число u + vi такое, что (u + vi)² = 3 – 4i. В данном случае a = 3, b = -4, поэтому уравнения (16) принимают вид

, .

Второе из равенств (15) запишется так: 2uv = - 4, uv =-2; это означает, что соответствующие зна­чения u и v имеют разные знаки. Так как u² = 4, v² = 1, то с учетом равенства uv = -2 находим, что u₁ = 2, v₁ = -1, u₂ = -2, v₂ = 1, т.е. 2 – i и -2 + i – значения квадратного корня из комп­лексного числа 3 – 4i.

Геометрическое изображение комплексного числа

В

-1

1

-i

i

0

x

y

(a,b)

(a,b)

Рис. 1

сякое комплексное число α = a + bi мы можем изображать как точку на плоскости с координатами a и b (рис. 1). Число α называют аффиксом этой точки. Плоскость, точки которой изображают комплексные числа, называют комплексной числовой плоскостью. Начало координат, которому соответствует число 0, называют нулевой точкой. При таком изображении комплексных чисел действительные числа изображаются точками оси абсцисс, точки же оси ординат представляют чисто мнимые числа. Поэтому ось абсцисс называют действительной осью, ось ординат – мнимой осью. Сопряженные комплексные числа α и изображаются точками, симметричными относительно действительной оси, противоположные комплексные числа α и –α симметричны относительно нулевой точки.

Комплексные числа и соответствующие им точки комплексной плоскости обозначают буквой z и пишут z = x + iy, где x – действительная часть (x = Rez), y – мнимая часть (y = Imz).

Модуль и аргумент комплексного числа

Комплексное число z = x + iy изобра­зим точкой z комплексной плоскости; точка z имеет координаты (x, y). Рассмотрим радиус-вектор этой точки (рис. 2). Модулем комплексного числа z называют длину г радиус-вектора данной точки. Модуль комплексного числа z обозначают через |z|. Следовательно, по определению

r = |z|, |z| 0. (17)

Поскольку г = (получено из формулы для расстояния между двумя точками на плоскости: 0 (0, 0) и z (x, y)), то

|z| = . (18)

Э

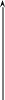
0

x

y

Рис. 2

φ

- φ

z

z

A

та формула выражает мо­дуль комплексного числа z = x + iy через его действительную и мнимую часть. Формула (18) имеет простой геометрический смысл: она выражает длину гипотенузы прямо­угольного треугольника с катетами |х| и |y| (см. рис. 2).

О

z=|z|

тметим, что модуль комплексного числа являет­ся неотрицательным действительным числом.

Аргументом комплексного числа z = x + iy назы­вают величину угла φ наклона радиус-вектора к положительной полуоси Ox. Аргумент комплексного числа z обозначают так: Argz. При изменении z этот угол может принимать любые действительные значения (как положительные, так и отрицательные; последние отсчитываются по часо­вой стрелке). Если модули двух комплексных чисел равны, а значения угла φ отличаются друг от друга на 2π, или на число, кратное 2π, то точки, соответст­вующие этим комплексным числам, совпадают; комп­лексные числа в этом случае равны между собой. Следовательно, аргумент комплексного числа z имеет бесконечное множество значений, отличающихся друг от друга на число, кратное 2π. Аргумент не опре­делен лишь для числа 0, модуль которого равен нулю: |0| =0. Среди значений аргумента комплексного чи­сла z 0 существует одно и только одно значение, за­ключенное между —π, +π, включая последнее значение. Его называют главным значением аргумен­та и обозначают argz. Итак, модуль и аргумент комплексного числа z удовлетворяют следующим соотношениям:

|z| 0, -π < argz π, Argz = argz + 2πn (n = 0, 1, 2, …).

Главное значение аргумента положительного действительного числа равно 0, главное значение аргумента действительного отрицательного числа равно π, главное значение аргумента мнимого числа bi (b > 0) равно π/2, главное значение аргумента мнимого числа –bi (b > 0) равно –π/2.

Выразим действительную и мнимую части комп­лексного числа z = x + iy через его модуль и аргу­мент. Пусть точка z изображает число z = x + iy (рис. 2). Из прямоугольного треугольника ОAz получаем

x = r cosφ, y = r sinφ, (19)

где r = |z|. Отсюда и из формул (17), (18) следует:

cosφ = , sinφ = , tgφ = .

Например: 1) найдём аргумент числа z = 1 – i. Так как Re z = 1, Im z = -1, то точка z = 1 – i лежит в IV четверти. Поэтому достаточно найти такое решение одного из последних уравнений , которое является углом в IV четверти. Рассмотрим уравнение cosφ = . Находим

cos φ = , φ = + 2kπ (k = 0, 1, 2, …);

2) найдём аргумент числа -1- i. Точка -1-i лежит в III четверти. Найдём такое решение уравнения tg φ = , которое является углом в III четверти. Находим

tg φ = 1, φ = + 2kπ (k = 0, 1, 2, …).

Характеристики

Список файлов реферата