Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

Известно, что движение является частным случаем аффинного преобразования, значит, движение под аффинным преобразованием, как композиция аффинных преобразований, также будет аффинным преобразованием.

13.1. Трансформация произвольного аффинного преобразования гомотетией

Выберем систему координат таким образом, чтобы центр гомотетии совпадал с началом координат, тогда 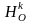будет задаваться аналитически следующим образом.

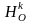Рассмотрим произвольную точку М(x, y, z), найдем ее образ при преобразовании . При гомотетии точка М переходит в точку М₁(x/k, y/k, z/k). Далее, при аффинном преобразовании g М₁ переходит в точку М₂( , , ). M₂ при гомотетии переходит в М₃( , ,

). Тогда - аффинное преобразование, аналитически оно задается следующим образом.

(34)

Мы получили, что

(35)

где - параллельный перенос, .

13.2. Трансформация косого сжатия гомотетией

Р

В₁

ассмотрим гомотетию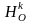 и косое сжатие g с осью q, направлением l и коэффициентом m. Найдем, что представляет собой трансформация косого сжатия гомотетией – 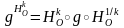, для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 7).

Т очка А при гомотетии перейдет в точку А₁, которая при косом сжатии перейдет в точку А₂ такую, что А₁А₂ || l, . Точка А₂ при гомотетии 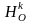перейдет в точку А₃. Заметим, что прямая – инвариантная прямая всей трансформации (по теореме о неподвижных прямых). Из точек А₁ и А₂ проведем перпендикуляры на прямую q – А₁В₁ и А₂В₂, а из точек А и А₃ – на прямую q₁ – АВ и А₃В₃. Тогда АВ и А₃В₃ – образы отрезков А₁В₁ и А₂В₂ при гомотетии 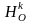, значит, , следовательно, . Мы получили, что при этой трансформации расстояние от точки А до прямой q₁ изменилось в m раз: . Причем из того, что А₁А₂ || l, следует, что AA₃ || l, потому что при гомотетии прямая переходит в параллельную ей прямую, значит, точка А сместилась в направлении l. Следовательно, в силу произвольности точки А, искомая трансформация есть косое сжатие с осью , направлением l и коэффициентом m.

13.3. Трансформация сдвига гомотетией

Рассмотрим гомотетию 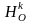и сдвиг g с осью q и коэффициентом m. Найдем, что представляет собой трансформация сдвига гомотетией – 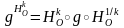, для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 8).

Т очка А при гомотетии перейдет в точку А₁, которая при сдвиге перейдет в точку А₂ такую, что А₁А₂ || q, . Точка А₂ при гомотетии 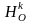перейдет в точку А₃. Заметим, что прямая – инвариантная прямая всей трансформации (по теореме о неподвижных прямых). Из точки А₁ проведем перпендикуляр на прямую q А₁В₁, а из точки А – на прямую q₁ – АВ. Тогда АВ – образ отрезка А₁В₁ при гомотетии 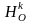, также АА₃ – образ отрезка А₁А₂ при гомотетии 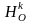, значит, и АА₃||А₁А₂||q||q₁, (потому что при гомотетии прямая переходит в параллельную ей прямую), следовательно, и АА₃||q₁. Мы получили, что при этой трансформации точка А смещается параллельно прямой q₁ на расстояние, пропорциональное ее расстоянию от прямой q₁: . Следовательно, в силу произвольности точки А, искомая трансформация есть сдвиг с осью и коэффициентом m.

14. Трансформация аффинного преобразования движением

14.1. Трансформация произвольного аффинного преобразования движением

14.1.1. Трансформация аффинного преобразования параллельным переносом

Данную трансформацию рассмотрим в пространстве. Пусть параллельный перенос задан вектором , (a, b, c). Рассмотрим произвольную точку М(x, y, z), найдем ее образ при преобразовании . При параллельном переносе точка М переходит в точку М₁(x-a, y-b, z-c). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂(a₁x + b₁y + + c₁z - aa₁ - bb₁ - cc₁ + d₁, a₂x + b₂y + c₂z - aa₂ - bb₂ - cc₂ + + d₂, a₃x + b₃y + c₃z - aa₃ - bb₃ - cc₃ + d₃). M₂ при параллельном переносе переходит в М₃ (a₁x + b₁y + c₁z - aa₁ - bb₁ - cc₁ + d₁ + a, a₂x + b₂y + c₂z - aa₂ - bb₂ - cc₂ + d₂ + + b, a₃x + b₃y + c₃z - aa₃ - bb₃ - cc₃ + d₃ + c) (п. 13). Тогда - аффинное преобразование, аналитически оно задается следующим образом.

(36)

Мы получили, что

, (37)

где (- aa₁ - bb₁ - cc₁ + d₁ + a, - aa₂ - bb₂ - cc₂ + d₂ + b, - aa₃ - bb₃ - cc₃ + d₃ + c).

14.1.2. Трансформация аффинного преобразования центральной симметрией

Рассмотрим центральную симметрию Z_O в пространстве, выберем систему координат таким образом, чтобы центр симметрии О совпал с началом координат, тогда О(0, 0, 0). Рассмотрим произвольную точку М(x, y, z), найдем ее образ при преобразовании . Т.к. центральная симметрия инволютивна, то . При центральной симметрии Z_O точка М переходит в точку М₁(-x, -y, -z). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂(-a₁x - b₁y - c₁z + d₁, -a₂x - b₂y - c₂z + d₂, -a₃x - b₃y - c₃z + d₃) (п. 13). M₂ при центральной симметрии Z_O переходит в М₃(a₁x + b₁y + c₁z - d₁, a₂x + b₂y + c₂z - d₂, a₃x + b₃y + c₃z - d₃). Тогда - аффинное преобразование, аналитически оно задается следующим образом.

(38)

Мы получили, что

, (39)

где (-2d₁, -2d₂, -2d₃).

14.1.3. Трансформация аффинного преобразования осевой симметрией

Рассмотрим осевую симметрию S_l в пространстве, выберем систему координат таким образом, чтобы ось симметрии l совпала с осью OZ, тогда S_l будет задаваться следующим образом. Рассмотрим произвольную точку М(x, y, z), найдем ее образ при преобразовании . Т.к. осевая симметрия инволютивна, то . При осевой симметрии S_l точка М переходит в точку М₁(-x, -y, z). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂(-a₁x - b₁y + c₁z + d₁, -a₂x - b₂y + c₂z + d₂, -a₃x - b₃y + c₃z + d₃) (п. 13). M₂ при осевой симметрии S_l переходит в М₃(a₁x + b₁y - c₁z - d₁, a₂x + b₂y - c₂z - d₂, a₃x + b₃y - c₃z - d₃). Тогда - аффинное преобразование, аналитически оно задается следующим образом.

(40)

14.1.4. Трансформация аффинного преобразования зеркальной симметрией

Рассмотрим зеркальную симметрию S_α – преобразование постраноства, выберем систему координат таким образом, чтобы плоскость симметрии α совпала с плоскостью XOY, тогда S_α будет задаваться следующим образом. Рассмотрим произвольную точку М(x, y, z), найдем ее образ при преобразовании . Т.к. зеркальная симметрия инволютивна, то . При зеркальной симметрии S_α точка М переходит в точку М₁(x, y, -z). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂(a₁x + b₁y - c₁z + d₁, a₂x + b₂y - c₂z + d₂, a₃x + b₃y - c₃z + d₃) (п. 13). M₂ при зеркальной симметрии S_α переходит в М₃(a₁x + b₁y - c₁z + d₁, a₂x + b₂y - c₂z + d₂, -a₃x - b₃y + c₃z - d₃). Тогда - аффинное преобразование, аналитически оно задается следующим образом.

(41)

14.2. Трансформация косого сжатия движением

К осое сжатие – частный случай родства, при котором каждая точка А плоскости смещается в некотором фиксированном направлении так, что ее расстояние от некоторой фиксированной прямой q изменяется в k раз: (рис. 9). [3]

Рассмотрим произвольное движение f и косое сжатие g с осью q, направлением l и коэффициентом k. Найдем, что представляет собой трансформация косого сжатия произвольным движением – , для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 10).

Точка А при произвольном движении f ^-1 перейдет в точку А₁, которая при косом сжатии перейдет в точку А₂ такую, что А₁А₂ || l, . Точка А₂ при движении f перейдет в точку А₃. Заметим, что прямая q₁ = f(q) – инвариантная прямая всей трансформации (по теореме о неподвижных прямых). Из точек А₁ и А₂ проведем перпендикуляры на прямую q – А₁В₁ и А₂В₂, а из точек А и А₃ – на прямую q₁ – АВ и А₃В₃. Тогда АВ и А₃В₃ – образы отрезков А₁В₁ и А₂В₂ при движении f, значит, АВ = А₁В₁ и А₃В₃ = А₂В₂ , следовательно, . Мы получили, что при этой трансформации расстояние от точки А до прямой q₁ изменилось в k раз: . Причем из того, что А₁А₂ || l, следует, что AA₃ || f(l), потому что при движении сохраняется параллельность прямых, значит, точка А сместилась в направлении f(l). Следовательно, в силу произвольности точки А, искомая трансформация есть косое сжатие с осью f(q), направлением f(l) и коэффициентом k.

14.3. Трансформация сдвига движением

Сдвигом называется аффинное преобразование плоскости, при котором произвольная точка А смещается параллельно фиксированной прямой q на расстояние, пропорциональное ее расстоянию от прямой q (рис. 11). - коэффициент сдвига. [3]

Р ассмотрим произвольное движение f и сдвиг g с осью q и коэффициентом k. Найдем, что представляет собой трансформация сдвига произвольным движением – , для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 12).

Точка А при произвольном движении f ^-1 перейдет в точку А₁, которая при сдвиге перейдет в точку А₂ такую, что А₁А₂ ||q, . Точка А₂ при движении f перейдет в точку А₃. Заметим, что прямая q₁ = = f(q) – инвариантная прямая всей трансформации (по теореме о неподвижных прямых); АА₃ – образ отрезка А₁А₂ при движении f, значит, АА₃ = А₁А₂, d(A₁, q) = d(A, q₁) и АА₃ ||q, тогда . Следовательно, в силу произвольности точки А, искомая трансформация есть сдвиг с осью f(q) и коэффициентом k.

15. Трансформация аффинного преобразования подобием

15.1. Трансформация косого сжатия подобием

Рассмотрим косое сжатие g с осью q, направлением l и коэффициентом m и подобие , где f – движение, найдем трансформацию g^h. . В силу ассоциативности композиции преобразований, . По доказанному в п. 13.2, есть g₁ - косое сжатие с осью , направлением l и коэффициентом m. Тогда По доказанному в пункте 14.2, g₁ ^f есть косое сжатие с осью f(q₁), направлением f(l) и коэффициентом m. Таким образом, вся искомая трансформация представляет собой косое сжатие с осью , направлением f(l) и коэффициентом m.

15.2. Трансформация сдвига подобием

Рассмотрим сдвиг g с осью q и коэффициентом m и подобие , где f – движение, найдем трансформацию g^h. . В силу ассоциативности композиции преобразований, . По доказанному в п. 13.3, есть g₁ - сдвиг с осью и коэффициентом m. Тогда По доказанному в пункте 14.3, g₁ ^f есть косое сжатие с осью f(q₁) и коэффициентом m. Таким образом, вся искомая трансформация представляет собой косое сжатие с осью и коэффициентом m.

16. Трансформация аффинного преобразования аффинным преобразованием

16.1. Трансформация косого сжатия произвольным аффинным преобразованием

Р ассмотрим произвольное аффинное преобразование и косое сжатие g с осью q, направлением l и коэффициентом k. Найдем, что представляет собой трансформация косого сжатия g произвольным аффинным преобразованием f – , для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 13).

Характеристики

Список файлов курсовой работы