63370 (597587), страница 5
Текст из файла (страница 5)
2, 4, 8 это гибридные микросхемы;
3 прочие микросхемы, в том числе, и плёночные.
Перед первым элементом обозначения может стоять буква или две буквы (русского алфавита), они не обязательны, но ими обозначают тип и материал корпуса микросхемы и возможности её применения. Например, буквой К обозначают микросхемы широкого применения в пластмассовом корпусе первого типа. Есть микросхемы специального применения, например, для устройств, эксплуатируемых в условиях тропического климата.
Второй элемент 2 или 3 цифры, ими обозначают порядковый номер серии микросхем. Всё множество выпускаемых отечественной промышленностью микросхем делится на серии. Серия ИМС это совокупность ИС единого конструктивно-технологического исполнения, выполняющих различные функции и предназначенных для совместного применения.
Третьим элементом в обозначении являются две русские буквы, первая из которых обозначает подгруппу ИС по функциональному назначению, а вторая буква соответствует виду ИС также по функциональному назначению микросхемы. Например, первая буква Л «говорит», что это ИС логических элементов (подгруппа логика), вторая буква А соответствует логическим элементам вида И-НЕ. В табл.1.2 приведены наиболее употребительные буквенные коды видов ИС по выполняемым функциям.
И
Рис.1.1. Система условных обозначений ИМС
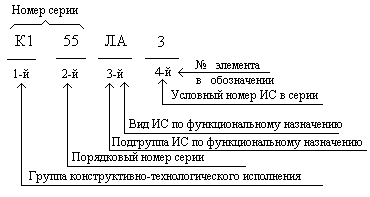 , наконец, 4-м элементом в обозначениях микросхем являются одна или две цифры, обозначающие условный номер микросхемы в рассматриваемой серии. Так, приведённый на рис.1.1 пример обозначения соответствует обозначению полупроводниковой микросхемы серии К155, широкого применения, в пластмассовом корпусе 1-го типа. В её состав входят 4 двухвходовых логических элементов вида И-НЕ (2И-НЕ).
, наконец, 4-м элементом в обозначениях микросхем являются одна или две цифры, обозначающие условный номер микросхемы в рассматриваемой серии. Так, приведённый на рис.1.1 пример обозначения соответствует обозначению полупроводниковой микросхемы серии К155, широкого применения, в пластмассовом корпусе 1-го типа. В её состав входят 4 двухвходовых логических элементов вида И-НЕ (2И-НЕ). Обычно четвёртым элементом в обозначении ИМС «зашифровывается» порядковый номер модификации элементов одного вида, различающихся числом входов и способом «организации» выхода.
Кроме названных обозначений, согласно ГОСТ 2.743-91 «Условные графические обозначения в электрических схемах. Элементы цифровой техники», используются другие двухбуквенные коды для обозначения функционального назначения микросхем, например: ИД декодеры- демультиплексоры, дешифраторы, ИР регистры, КП коммутаторы дискретных сигналов и так далее. В частности, буква И соответствует подгруппе микросхем, используемых для построения вычислительных цифровых устройств.
Различные серии ИС отличаются количеством микросхем и их номенклатурой (типономиналами). Типономинал ИС конкретное условное обозначение, содержащее основные сведения о микросхеме. В процессе развития технологии количество типономиналов ИМС конкретной серии может увеличиваться.
Среди серий микросхем наиболее функционально развиты ИМС транзисторно-транзисторной логики (ТТЛ и ТТЛш). Эти серии характеризуются широкой номенклатурой ИС, поэтому изложение учебного материала будем в основном иллюстрировать примерами этих микросхем.
В указанном выше ГОСТе содержатся также условные графические обозначения логических элементов и приведены правила формирования УГО более сложных логических элементов и модулей. Поэтому следует, прежде всего, ознакомиться с указанным ГОСТом.
Таблица 1.2
Условное обозначение функций логических элементов
| Вид ИС | Обозначение |
| Элементы И-НЕ | ЛА |
| Элементы И-НЕ /ИЛИ-НЕ | ЛБ |
| Расширители по ИЛИ | ЛД |
| Элементы ИЛИ-НЕ | ЛЕ |
| Элементы И | ЛИ |
| Элем. И-ИЛИ-НЕ/И-ИЛИ | ЛК |
| Элементы ИЛИ | ЛЛ |
| Элементы ИЛИ-НЕ/ИЛИ | ЛМ |
| Элементы НЕ | ЛН |
| Прочие элементы | ЛП |
| Элементы И-ИЛИ-НЕ | ЛР |
| Элементы И-ИЛИ | ЛС |
1.3.2. Применение булевой алгебры для описания
логических элементов и устройств
Как уже было отмечено выше, функционирование логических элементов можно описать логическими (булевыми) функциями. В свою очередь логические функции можно определить (задать), перечислив все условия, при которых функция принимает значение лог.1, т.е. по условиям истинности, так и по условиям ложности (значения лог.0). Аналогично, рассматривая работу логического (какого-либо) элемента, можно перечислить все условия, при которых на выходе появляется сигнал лог.1, либо условия, когда на выходе элемента будет присутствовать сигнал лог.0. В этом заключается принцип дуальности (двойственности) в описании логических устройств.
В технике, при описании работы различных устройств, широко используется понятие «активного», в противоположность ему, «неактивного» значения какого-либо сигнала. При этом под активным значением (уровнем) сигнала понимается такое действие, которое вызывает на выходе устройства желаемое действие или, по-другому, устройство оказывает активные действия на внешние устройства. Наоборот, неактивные действия оказывают пассивное действие на внешние устройства. Так, в логике обычно акцентируют внимание на истинности высказываний, поэтому истинность высказываний следует считать по умолчанию их активным значением. Аналогично, при описании технических устройств можно акцентировать внимание на условиях их «срабатывания» либо на условиях «несрабатывания».
Соглашения, при которых сигнал лог.1 считается активным, называют соглашениями «положительной » логики. Наоборот, когда за активное значение принимается уровень лог.0, такие соглашения называют соглашениями «отрицательной » логики. Как правило, за сигнал лог.1 принимается более «высокий» уровень, а за сигнал лог.0 «низкий» уровень сигналов. Например, при использовании ИМС ТТЛ сигналом лог.1 считается напряжение не менее +2,4 В, а сигналом лог.0 напряжение больше нуля, но не больше 0,4 В. Это стандартные уровни сигналов в устройствах на ИМС ТТЛ.
Описания, составленные при соглашениях положительной логики и при соглашениях отрицательной логики, логически эквивалентны, так как описывают одно и тоже устройство. Однако сложность технической реализации логических устройств в зависимости от выбранного соглашения может оказаться существенно различной. Поэтому всегда возникает проблема выбора способа описания с целью получения наиболее простого технического решения.
Как уже было сказано, основными функциями алгебры логики являются функции двух переменных. Можно составить эти функции чисто формально, придавая аргументам всевозможные значения (комбинации их значений), и затем придать функциям так же всевозможные значения. Поскольку и аргументы и функции могут принимать только два значения, то нетрудно определить число комбинаций, составленных из аргументов, и число всех возможных функций. Пусть число аргументов будет n, а количество их комбинаций N, тогда
N = 2n. (1.1)
Число же всевозможных логических функций тогда можно рассчитать по формуле
M = 2N =  . (1.2)
. (1.2)
Как видно из формулы (1.2), число булевых (логических) функций быстро растёт с увеличением числа аргументов n. Так, при n =2 получим N=22=4, а М=24=16, т.е. шестнадцать логических функций от двух аргументов.
В табл. 1.3 приведены названия и обозначения функций, их значения на том или ином наборе значений аргументов a и b, а также алгебраические выражения этих функций в дизъюнктивной совершенной нормальной форме (ДСНФ) и конъюнктивной совершенной нормальной форме (КСНФ).
Из анализа этой таблицы следует, что среди множества приведённых функций есть функции-константы «нулевая» и «единичная», функции «повторения» и «инверсии» (функции НЕ) входных переменных a и b, фактически являющиеся функциями одного аргумента, и есть функции, которые существенно зависят от двух аргументов.
В приведённых алгебраических выражениях знаком + (плюс) обозначена операция логического сложения (дизъюнкции), чертой над переменной или над логическим выражением обозначена операция инверсии, а символы логического умножения (произведения) пропущены.
Таблица 1.3
Логические функции двух аргументов
| № п/п | Название функции | Значения функции при значениях аргументов | Обозначение | Алгебраические формы функций | |||||||
| а b | 0 | 0 | 1 | 1 | ДСНФ | КСНФ | |||||
| 0 | 1 | 1 | 0 | ||||||||
| V0 | Нулевая | 0 | 0 | 0 | 0 | 0 |
|
| |||
| V1 | Запрет b | 0 | 0 | 0 | 1 | ab |
|
| |||
| V2 | Конъюнкция (И) | 0 | 0 | 1 | 0 | a&b или ab | ab |
| |||
| V3 | Повторение а | 0 | 0 | 1 | 1 | а |
|
| |||
| V4 | Запрет а | 0 | 1 | 0 | 0 | ba |
|
| |||
| V5 | Неравнозначность | 0 | 1 | 0 | 1 | ab |
|
| |||
| V6 | Повторение b | 0 | 1 | 1 | 0 | b |
|
| |||
| V7 | Дизъюнкция (функция ИЛИ) | 0 | 1 | 1 | 1 | a+b |
| a+b | |||
| V8 | Пирса (ИЛИ-НЕ) | 1 | 0 | 0 | 0 |
|
|
| |||
| V9 | Инверсия b (НЕ ) | 1 | 0 | 0 | 1 |
|
| ||||
| V10 | Равнозначность | 1 | 0 | 1 | 0 |
|
|
| |||
| V11 | Импликация b | 1 | 0 | 1 | 1 | ba |
|
| |||
| V12 | Инверсия а | 1 | 1 | 0 | 0 |
|
| ||||
| V13 | Шеффера (И-НЕ) | 1 | 1 | 0 | 1 |
|
|
| |||
| V14 | Импликация а | 1 | 1 | 1 | 0 | ab |
|
| |||
| V15 | Единичная | 1 | 1 | 1 | 1 | 1 |
|
| |||
Функции-константы фактически выражают независимость от аргументов и, в то же самое время, их можно считать «функциями» от большого числа аргументов. Обратите внимание, нулевая функция не имеет ДСНФ, поскольку она никогда не принимает значение лог.1, а единичная функция не имеет КСНФ, так как она никогда не принимает значение лог.0. Отсюда следует вывод, что ДСНФ соответствует описанию (заданию) логических функций по условиям истинности (по лог.1), а КСНФ по условиям ложности (по лог.0). Любая логическая функция, кроме функций-констант, имеет как ДСНФ, так и КСНФ. Это соответствует тому, что любое логическое устройство (сколь сложно оно ни было бы) можно описать по условиям срабатывания и по условиям несрабатывания.













