Book5 (563558), страница 6
Текст из файла (страница 6)
Δt’KP = Р/σ'Σ= 10/0,753= 13,3 ○С.
Разность температурных перегревов
| Δt’K - Δt’KP | = | 10- 13,3 |=3,3 °С> (1 ...2) "С.
Следовательно, требуется выполнить расчет во втором приближе-
нии.
Перегрев корпуса во втором приближении Δt"K = Δt' =13,3°C.
Температура корпуса t"K=60+13,3=73,3°С. Среднее значение темпе-
202
ратуры окружающей среды t"CP= 0,5 (60 + 73,3) = 66,7 ○С. Теплофизиче-
ские параметры воздуха для t"CP =66,7○С: λ"в=2,95Вт/м•○С ;
ν"=19,67•10-6м2/с; β"=2,94•10-31/°С.Критерий Gr"=98,96•104, критерий Рr " = 0.7, Gr "• Pr " = 69,28 • 10 4. Коэффициенты теплообмена
C=0.54, n=0,25. Критерий Nu"=0,54(69,28-104)0,25=15,6. Конвективный коэффициент теплопередачи во втором приближении
α"к = 15,6 • 2,96 • 10 -2 /0,1 = 4,59 Вт/( м 2 •˚С); коэффициент теплопередачи излучением а"л = 8,18 Вт/(м -°С), эквивалентная тепловая проводимость
σ "Σ = (4,59+ 8,18) 0,06 = 0,766 Вт/°С. Расчетное значение
перегрева во втором приближении Δt"кр = 10/0,766= 13,05°С. Расхождение расчетного значения перегрева во втором приближении с заданным составляет 0,25°С. Следовательно, можно принять, что перегрев
корпуса блока ΔtK= 13 °С, среднеповерхностная температура
tK = tc + ΔtK=60+13 = 73°C.
Метод тепловой характеристики состоит в построении по рас-
чётным данным зависимости Δtj =f(P), по которой для любого значения теплового потока Р можно найти перегрев и температуру j-й точки
или области конструкции.

чение перегрева Δt’j , как и в мето-
де последовательных приближений; находят эквивалентную тепловую проводимость между j-й точкой и окружающей средой σ’Σ, затем тепловой поток Р' = σ’Σ,Δt’j, который способна рассеять конструкция при данных усло-
виях теплообмена. Значения Δt’j и
Рис. 5.22. Общий вид тепловой характеристики
Р' являются координатами однойточки, лежащей на тепловой харак-
теристике, второй точкой служит начало координат. Таким образом, тепловая характеристика представляет собой прямую, проходящую через начало координат и точку с ко-
ординатами Δt’j и Р' (рис. 5.22). По тепловой характеристике может быть найден перегрев и температура j'-й точки или области конструкции при любом заданном значении теплового потока.
203
Пример 5.4. По условиям примера 5.3 методом тепловой характери-
стики определить среднеповерхностную температуру корпуса блока.

В примере 5.3 для начального
перегрева корпуса Δ tK' =10 °С была
Рис. 5.23. Тепловая характеристика
блока РЭС
найдена эквивалентная тепловая
проводимость «корпус — окружающая среда» σ'Σ = 0,753 Вт/°С. Тепловой поток, который может рассеять поверхность корпуса блока, Р' = 0,753 • 10 = 7,53 Вт.
Тепловая характеристика блока
приведена на рис. 5.23. По характеристике для заданного теплового потока Р = 10 Вт находим ΔtK = 13,1˚С, tK =60+13,1 = 73,1 °С.
Исследования показывают, что тепловые режимы РЭС характеризу-
ются достаточно высокой стабильностью и зависят от ряда факторов,
относящихся к самой конструкции (геометрических размеров, коэффициента заполнения, структуры нагретой зоны, значения теплового потока) и к условиям эксплуатации (температуры и давления окружающей среды).
Изучение влияния на показатели теплового режима определяющих
факторов с помощью физических и теоретических тепловых моделей
конструкции (при изменении этих факторов в широких пределах) по-
зволило установить закономерности, положенные в основу коэффици-
ентного метода расчета тепловых режимов конструкций РЭС опреде-
ленных классов.
Математической базой этого метода служат следующие выкладки.
Пусть для некоторой типовой конструкции при номинальных значе-
ниях определяющих параметров х 01, х 02, ..., х0n тепловая характеристика имеет вид
t0 = t0(X01, X02, ..., X0n) .
При бесконечно малых изменениях каждого параметра показатель
теплового режима получит приращение или в конечных приращениях
204
или в конечных приращениях
где Ai . коэффициент влияния параметрах x0i на показатель теплового
режима; Δt0i— приращение показателя теплового режима, обусловленное изменением параметра x0i
Новое значение показателя теплового режима можно представить в
При условии, что Δ t 0i /t0 <<1
Ввиду того что t0 + Δt0i=ti,— показатель теплового режима при
изменении параметра х0i ,а отношение ti/t0=Ki — парциальный ко-
эффициент показателя,
Так как одним из основных показателей теплового режима является
температурный перегрев, используемое в коэффициентном методе
расчетное соотношение записывается в виде
Начальное значение перегрева Δt0 определяют по тепловой харак-
теристике для типовой конструкции. Тепловая характеристика строится в координатах Δt , поверхностная плотность теплового потока Ps =Р /S, где S — площадь поверхности теплообмена.
Значения коэффициентов Ki обычно даются в виде графиков зави-
симостей от того или иного определяющего параметра.
На рис. 5.24 приведены графики для определения коэффициентов
площади поверхности теплообмена конструкции Ks (а), степени черно-
205

Рис. 5.24. Графики для определения коэффициентов (а, б, в)
и тепловая характеристика типовой конструкции (г)
ты поверхности Кε (б), давления окружающей среды Кн (в) и тепловая
характеристика типовой конструкции.
При использовании коэффициентного метода следует иметь в виду,
что область его применения ограничивается тем классом конструкций,
для которых определены коэффициенты.
Пример 5.5. Определить температуру корпуса блока РЭС, имеюще-
го размеры 0,176x0,095x0,072 м, при тепловом потоке Р = 16 Вт, давле-
нии окружающей среды Н = 760 мм рт. ст. и температуре окружающей
среды t с = 20 ˚С. Корпус окрашен эмалевой краской ε к = 0,92.
Площадь поверхности корпуса
SК = 2(0,176• 0,095+0,176•0,072+0,095•0,072) = 0,0724 м2.
206
Плотность теплового потока
PS = P/SK= 16/0,0724= 221 Вт/м 2.
По тепловой характеристике рис. 5.24, г находим Δt0 = 21,9 °С. Из
графиков (рис. 5.24, а, б, в) определяем KS = 0,93, Кε = 1.0, KH=1.0.
Перегрев поверхности корпуса
ΔtK = Δt0KSKεKH=21,9•0,93• 1,0•1,0 = 20,4˚C.
Среднеповерхностная температура корпуса
tK = tc + Δtk = 20 + 20.4=40.4°C.
5.3. Системы охлаждения конструкций РЭС
5.3.1. Классификация и эффективность систем охлаждения
Системой охлаждения называется совокупность устройств и конст-
руктивных элементов, используемых для уменьшения локальных и об-
щих перегревов.
Системы охлаждения принято классифицировать по способу пере-
дачи тепла, виду теплоносителя и характеру контакта теплоносителя и
источника тепла.
В зависимости от способа передачи тепла и вида теплоносителя си-
стемы охлаждения подразделяются на кондуктивные, воздушные, жид-
костные, испарительные, комбинированные.
В зависимости от характера контакта теплоносителя и источника
тепла'различают системы охлаждения прямого и косвенного действия.
Кроме того, все системы охлаждения принято делить на системы
общего и локального назначения, с замкнутым (теплоноситель цирку-
лирует в системе охлаждения) и разомкнутым (теплоноситель выбра-
сывается из системы охлаждения) циклами.
Воздушные системы охлаждения, в свою очередь, подразделяются
на системы естественного воздушного охлаждения, системы охлажде-
ния с естественной вентиляцией и системы принудительного воздуш-
ного охлаждения.
Жидкостные и испарительные системы охлаждения также делятся
на системы естественного жидкостного (испарительного) охлаждения
и системы принудительного жидкостного (испарительного) охлаждения.
Особый класс представляют собой системы охлаждения, основан-
ные на использовании эффекта Пельтье.
207
Эффективность систем охлаждения может быть оценена поверхно-
стной плотностью теплового потока, уносимого теплоносителем из
РЭС.
Для различных систем охлаждения плотность теплового потока ха-
рактеризуется величинами, представленными в табл. 5.7.
Таблица 5.7
| Вид систем охлаждения | Плотность теплового потока Р S , | Вт/см2 |
| Естественное воздушное охлаждение | 0,2 | |
| Принудительное воздушное охлаждение | 1,0 | |
| \ Жидкостные системы охлаждения | 20 | |
| Испарительные | 200 | |
5.3.2. Выбор способа охлаждения на ранних стадиях разработки
Ввиду того что способ (система) охлаждения в значительной мере
определяет структуру конструкции РЭС, уже на ранних стадиях разра-
ботки важно правильно выбрать способ охлаждения. Выбранный спо-
соб охлаждения должен обеспечить нормальный тепловой режим кон-
струкции РЭС.
Если в выборе способа охлаждения будет допущена ошибка, то труд
большого коллектива разработчиков окажется напрасным, а сроки раз-
работки конструкции и ее стоимость существенно возрастут. Посколь-
ку на ранних стадиях разработчики располагают минимальной инфор-
мацией о конструкции, то становится очевидной ответственность и од-
новременно сложность задачи выбора системы охлаждения.
Начальное представление о способе охлаждения можно составить
по данным табл. 5.7. Однако при решении практических задач выбор
системы охлаждения производится по графикам рис. 5.25, которые ог-
раничивают области целесообразности применения того или иного
способа охлаждения. Эти области построены по результатам обработки
статистических данных о показателях тепловых режимов реальных кон-
струкций РЭС, расчетов показателей тепловых режимов по тепловым
моделям и экспериментальных данных, полученных на макетах.
Исходными данными для выбора системы охлаждения служат:
тепловой поток Р, рассеиваемый конструкцией;
диапазоны возможного изменения температуры окружающей среды
t с min ….t с mах
пределы изменения давления окружающей среды Нтах.. • Hmin;
допустимые рабочие температуры элементов t эi;
208

Рис. 5.25. Диаграмма выбора системы охлаждения
геометрические размеры корпуса конструкции LX , LY , LZ , :
коэффициент заполнения объема конструкции k З;
время непрерывной работы конструкции τ.
Перечисленные исходные данные, за исключением коэффициента
заполнения конструкции, обычно указываются в техническом задании
на разработку и известны. Коэффициент заполнения может быть вы-
бран на основе опыта конструирования подобных РЭС.
Поскольку графики рис. 5.25 справедливы лишь для стационарного
режима, то необходимо знание времени непрерывной работы для опре-
деления режима.
Пределы изменения давления окружающей среды задают условия,
при которых тепловой режим является наиболее тяжелым.
Основным показателем, определяющим области целесообразного
применения способа охлаждения на рис. 5.25, служит плотность тепло-
вого потока
PS=PKH/SK
где KH— коэффициент, учитывающий давление окружающей среды;
SK=2[LXLY+(LX+LY)LZK3]—площадь поверхности теплообмена.
Вторым показателем является допустимый перегрев в конструкции
Δtдоп = tЭ min-tC
где tЭ min — допустимая рабочая температура наименее теплостойкого
радиоэлемента; t c — температура окружающей среды.
209
Для естественного воздушного охлаждения t с = t с шах, т.е. соответ-
ствует максимальной температуре окружающей среда, заданной в ТЗ.
Для принудительного охлаждения t с = tВХ, т.е. соответствует темпера-
туре воздуха (жидкости) на входе системы охлаждения.
Значения РS и Δt являются координатами точки, попадающей в одну из областей на рис. 5.25, каждой из которых соответствует один или
несколько способов охлаждения.
Незаштрихованные области на рис. 5.25 относятся к следующим
способам охлаждения: 1 — естественное воздушное, 3 — принудитель-
ное воздушное, 5 — принудительное жидкостное, 9 — принудительное
испарительное.
Заштрихованные области допускают использование нескольких
• способов охлаждения: 2 — естественное и принудительное воздушное,
4 — принудительное воздушное и жидкостное, 6 — принудительное
жидкостное и естественное испарительное, 7 — принудительное жид-
костное, принудительное и естественное испарительное, 8 — естест-
венное и принудительное испарительное.
Графики на рис. 5.25, соответствующие Δt> 100°С, используются
для выбора способа охлаждения больших элементов (трансформато-
ров, дросселей, транзисторов на радиаторах и т.п.), поскольку допусти-
мые температуры их поверхностей относительно высоки. Нижняя часть
диаграммы применяется для выбора способа охлаждения блоков и уст-
ройств РЭС.
Если показатели Р Sи Δt доп для конкретной РЭА (ЭДЭА) попадают в
незаштрихованные области рис. 5.25, то способ охлаждения определяется однозначно.
Для заштрихованных областей, где возможно использование двух или
трех различных способов охлаждения, задача выбора того или иного спо-
соба усложняется. Чтобы найти правильное решение, необходимо вос-
пользоваться вероятностными кривыми, которые связывают показатели
Р S , Δt ДОП и вероятности обеспечения заданного теплового режима при
различных условиях теплообмена. Для области 2 (воздушное охлажде-
ние) вспомогательные вероятностные графики приведены в [61].
Если геометрические размеры конструкции не заданы, то площадь
поверхности теплообмена можно найти приближенно, используя све-
дения об элементной базе конструкции и коэффициенты дезинтегра-
ции массы или объема. Задача сводится к ориентировочному определе-
нию объема конструкции, через который вычисляется площадь поверх-
ности. Один из возможных путей решения задачи состоит в следую-
щем: через массу радиоэлементов m эл и коэффициент дезинтеграции
210
массы находят массу конструкции тK =qm•mЭЛ затем определяют
объем конструкции VK = m K /m 0, где m 0 — плотность конструкции, и
площадь поверхности корпуса SK=6(VK)2/3 . Если известны данные о
суммарном установочном объеме радиоэлементов VЭЛ, то объем конст-
рукции VK = q VVэл, где q v— коэффициент дезинтеграции объема.
5.4. Особенности конструкций РЭС
с кондуктивными системами охлаждения
Кондуктивные системы охлаждения основаны на контактном спосо-
бе передачи тепла за счет теплопроводности элементов конструкции.
Структурная схема цепи теплопередачи в кондуктивной системе ох-
лаждения приведена на рис. 5.26. Тепло, выделяемое источником, че-
рез неразъемный тепловой контакт передается на теплоотвод (тепло-
вую шину), с которой через тепловой разъем поступает на тепловой
сток.

Рис. 5.26. Структура кондуктивной цепи теплопередачи
В идеальной кондуктивной системе теплоемкость стока должна
быть бесконечно большой. Поскольку такие теплостоки не реализуемы
практически, в реальных конструкциях РЭС кондуктивные цепи тепло-
передачи, как правило, заканчиваются теплообменниками, отдающими
тепло окружающей среде или другому теплоносителю.
Высокая эффективность кондуктивных систем охлаждения дости-
гается при малом тепловом сопротивлении цепи теплопередачи между
источником тепла и окружающей средой. Поэтому при разработке кон-
струкций РЭС с кондуктивными системами охлаждения прежде всего
необходимо обратить внимание на тепловые контакты, конструкцию
тепловой шины и теплообмен с окружающей средой или иным тепло-
носителем в теплообменнике.
211
5.4.1. Моделирование тепловых контактов в кондуктивных цепях

Структура теплового контакта изображена на рис. 5.27. В контакте
тепло от нагретой поверхности к холодной передается теплопроводно-
стью фактического контакта 1 и среды
2, заполняющей микронеровности по-
верхностей. Эффективность теплопе-
редачи излучением ввиду малой разно-
сти температур между нагретой и хо-
лодной поверхностями низка. Поэтому
теплопередача излучением через среду
не учитывается.
Рис. 5.27. Контакт плоских
поверхностей:
1 — контакт; 2 — среда
Предполагается, что пятна фактиче-
ского контакта контактирующих повер-
хностей распределены равномерно по
всей поверхности контакта. Все пятна
имеют форму круга с одним и тем же
радиусом, не изменяющимся при изме-
нении нагрузки. Термическое сопро-
тивление окисной пленки на контактирующих поверхностях мало.
Тепловое сопротивление контакта
Rк = Р/Δtк=1/(σм+σс), (5.42)
где Р — тепловой поток, протекающий через контакт; Δ tK — разность
температур контактирующих поверхностей; σм — тепловая проводи-
мость, определяемая фактическими контактами; σс — тепловая прово-
димость среды.
Удельное (отнесенное к площади) сопротивление фактического
контакта
где φ— коэффициент стягивания теплового потока к пятнам фактиче-
ского контакта; λм = 2λ,1λ-2/(λ,1λ2) — эквивалентный коэффициент теплопроводности фактического контакта (λ1 , λ 2 — коэффициенты теплопроводности материалов); η = S ФК/S к— относительная площадь фактического контакта.
Определение параметров η и φ представляет собой сложную зада-
чу. Поэтому при расчете удельного сопротивления фактического кон-
0 8
такта R м. уд находят отношение η/φ=(рВ/Е)0.8 , где р — удельное
212
Рис. 5.28. График зависимости
коэффициента В от шероховатости
контактирующих поверхностей

эффициент, характеризующий
геометрические свойства по-
верхностей; Е — модуль упру-
гости материала. Выражение
для отношения η/φ справед-
ливо для поверхностей с чис-
тотой обработки от 3-го до
10-го класса, материалов с мо-
дулем упругости Е > 1010 Па и
при относительных нагрузках
на контактных поверхностях
р/Е=5•10-6...5•10-4. Значение коэффи
циента В находят из графика рис.5.28.
После подстановки в формулу (5.43) выражения для η/φ формула
расчета удельного сопротивления фактического контакта принимает
вид
Rм.уд=10-4-[2.12λM(рВ/Е)0.8]-1м2К/Вт.
Тепловая проводимость прослойки межконтактной среды σ с. уд =

= λС/δэкв , где λС — коэффициент теплопроводности среды; δэкв=
=(hСР1+hСР2)(1-mh) — эквивалентное расстояние между контактирующими поверхностями; hСР1 и hСР2 — средние высоты микронеровностей контактирующих поверхностей; т h — коэффициент заполнения профиля микронеровностей.
Значение ( 1 -т h ) находят с помощью графика рис. 5.29.
После того как величины R м. уд
и σС. УД определены, можно найти тепловую проводимость контакта
σк = (1/R м.уд + σс.уд)Sк.
где S к — площадь контакта.
Рис. 5.29. Зависимость коэффициента
(1 - m h) от суммы средних высот микро-
неровностей
Таким образом, величина теп-
ловой проводимости контакта за-
висит от коэффициентов тепло-
проводности материалов контакти-
рующих поверхностей, теплофизи-
ческих свойств межконтактной
213
среды, качества обработки контактирующих поверхностей, удельного
давления в контакте и площади контакта.
Для металлических поверхностей удельная тепловая проводимость
контакта определяется физико-механическими свойствами материа-
лов, чистотой обработки контактирующих поверхностей и удельным
давлением. При удельном давлении более 2000 Н/см2 , что характерно,
например, для резьбовых соединений, удельная тепловая проводи-
мость контакта практически не зависит от давления. Значения удель-
ной тепловой проводимости для некоторых контактирующих материа-
лов с шероховатостью поверхности R z = 20 и удельным давлением в
контакте 1000 Н/см2 приведены в табл. 5.8.
Таблица 5.8
| Материал контактирующих пар | σуд•104, Вт/(м2∙К) |
| Медь — алюминий | 12,5 |
| Медь — медь | 10 |
| Медь — латунь | 5,5 |
| Медь — сплав Д16Т | 5,0 |
| Сплав Д16Т — сплав Д16Т | 4,0 |
| Сталь — медь | 1,2 |
| Сталь — сплав Д16 | 0,83 |
| Сталь — сталь | 1,5 |
| Сталь — сталь (резьбовое соединение) | 0,17 |
| Металл — краска — металл | 0,05 |
| Металл — стекло | 3... 6,4 |
Используя данные табл. 5.8, можно для приведенных пар контакти-
рующих поверхностей провести оценку тепловой проводимости контакта , как σК =σУД. •SK где SK — площадь поверхности контакта.
5.4.2. Конструкции контактов в кондуктивных системах охлаждения
Кондуктивные цепи передачи тепла содержат два вида тепловых
контактов: неразъемные и разъемные.
Неразъемные тепловые контакты характерны для конструкций фун-
кциональных ячеек и представляют собой звено теплопередачи от теп-
ловыделяющего элемента к теплоотводящей шине. Тепловой контакт
обычно обеспечивается за счёт пайки, сварки и склеивания мест соеди-
214
нений, а также с помощью заклепок и винтов. В последних случаях для
уменьшения теплового сопротивления рекомендуется заполнять кон-
такты теплопроводящими пастами (например, КПТ-8) или клеями, ис-
пользовать в контактах пластичные прокладки из меди, свинца и алю-
миния. Применение теплопроводящих паст эффективно при шерохова-
тости контактирующих поверхностей выше R Z= 20 и позволяет снять
зависимость теплового сопротивления контакта от удельного давле-
ния.
В конструкциях функциональных ячеек на интегральных микросхе-
мах неразъемные тепловые контакты образуют корпуса микросхем с
теплоотводящими шинами.

Рис. 5.30. Установка микросхемы на
теплоотводящую шину

Вариант установки микросхемы в
корпусе типа 4 на теплоотводящую
шину показан на рис. 5.30, Теплоотво-
дящая шина 4 монтируется на печат-
ной плате 3 со стороны расположения
контактных площадок для пайки вы-
водов микросхем. Микросхема 1 при-
клеивается к шине, выводы микросхе-
мы распаиваются на контактные пло-
щадки 2 печатной платы. Материалом для теплоотводящих шин и кондуктивных теплостоков в виде металлических оснований служат сплавы алюминия, медь и ее сплавы. Применение теплоотводящих шин и металлических оснований позволяет снизить перегрев корпусов микросхем при естественном воздушном охлаждении конструкций приблизительно на (10...20)%. Для достиженияуказанного эффекта толщина шин и
оснований из сплавов алюминия должна быть не менее 1 мм, из меди и ее сплавов — не менее 0,5 мм.
Рис. 5.31. Установка микросхем на
металлические основания:
а — микросхема в корпусе типа 1;
б — микросхема в корпусе типа 4
Установка микросхем в корпусах
типов 1 и 4 на металлические основа-
ния производится согласно рис. 5.31.
Основание наряду с функцией кон-
дуктивного теплостока обычно вы-
полняет роль несущего элемента кон-
струкции. На основании закрепляется
печатная плата 2, пайка выводов мик-
росхем производится в отверстиях
(рис. 5.31,а) или окнах (рис. 5.31,6),
выполненных в основании. Как и в
случае с теплоотводящей шиной,
215
микросхемы для уменьшения теплового сопротивления между основа-
нием и корпусами устанавливаются на основании с помощью клея. Ве-
личина теплового сопротивления контакта зависит от теплопроводно-
сти клея. При увеличении коэффициента теплопроводности клея от
0,2 до 1,8 Вт/(м • К) перегрев микросхем, установленных на алюминие-
вых основаниях, снижается приблизительно на 10%, на медных основа-
ниях — на 23%.
Кондуктивные теплостоки в виде металлических рамок с планками
и оснований используются в конструкциях функциональных ячеек
цифровых РЭС на бескорпусных микросборках Микросборки закреп-
ляются на планках металлических рамок (конструкции односторонней
и сдвоенной функциональных ячеек) и основаниях (двухсторонняя
функциональная ячейка) с помощью клея.
В конструкциях СВЧ-узлов подложки микросборок выполняются из
материалов с высоким коэффициентом теплопроводности (поликор,
брокерит-9) и крепятся к основанию-теплоотводу или с помощью пай-
ки по металлизированной поверхности подложки, или одним из меха-
нических способов, обеспечивающих надежный тепловой электриче-
ский контакт.

Рис. 5.32. Фрагмент
конструкции СВЧ-устройства
на микросборках
Фрагмент конструкции СВЧ-устройст-
ва на микросборках приведен на рис. 5.32.
Бескорпусные СВЧ-микросборки 1 припа-
иваются к основанию — теплоотводу 3.
Мощный транзистор 2 размещается в спе-
циальном углублении непосредственно на
основании и закрепляется с помощью пай-
ки по металлизированной поверхности
подложки.
Разъемные тепловые контакты (тепло-
вые разъемы) обеспечивают сток тепла с
тепловых шин и металлических оснований
на теплообменник. В конструкциях РЭС с естественным воздушным охлаждением функции теплообменника выполняет корпус или элементы конструкции с развитой поверхностью (радиаторы). Включение теплового разъема создает непрерывную кондуктивную цепь теплопередачи «источник тепла — теп л о отводящая шина — тепловой разъем — корпус». Однако все разработанные и применяемые в конструкциях РЭС тепловые разъемы имеют недостатки: сложность конструкции, неудобство в эксплуатации, низкая производственная технологичность и др. Следует также иметь в виду, что использование тепловых разъемов ведет к ухудшению массогабаритных показателей конструкций РЭС.
216
Тепловые разъемы принято классифицировать по типу рабочего
элемента, замыкающего цепь теплопередачи от функциональной ячей-
ки 1 к теплообменнику 2 (рис. 5.33); рабочими элементами тепловых
разъемов служат ребро, паз, цилиндр, конус, клин и плоскость.


а — ребро; б — паз; в — цилиндр; г — корпус; д — клин; е — плоскость
Величина теплового сопротивления в разъеме определяется пло-
щадью поверхности теплопередачи (рис. 5.33, а), повышением точно-
сти соединения (рис. 5.33, б, в) и усилием сжатия поверхностей (рис.
5.33. г. д. е).
предусмотрен канал 1 системы принудительного жидкостного охлаждения .Конструкция обладает низким тепловым сопротивлением по всей плате (0.3…0.45К/Вт) и обеспечивает возможность оператив
ной замены ячеек в устройствах.
Рис. 5.34. Конструкция ФЯ
с тепловым разъемом
217
5.4.3. Основы расчета радиаторов
В кондуктивных системах охлаждения функции теплообменников с
окружающей средой часто выполняют радиаторы — элементы системы
охлаждения с развитой поверхностью теплообмена. Поверхность теп-
лообмена радиаторов увеличивается за счет их оребрения. С поверхно-
сти ребер тепловой поток передается в окружающее пространство кон-
векцией и излучением. При этом величина теплового потока определя-
ется выражением
P = KPSPK(t-tC),
где (. — коэффициент теплопередачи; КP — коэффициент эффективности ребра; Sр — площадь поверхности радиатора; t — среднеповерхностная температура радиатора; t c — температура окружающей среды.
Эквивалентный коэффициент теплопередачи . обусловлен кондуктивной теплопередачей через слой краски или покрытия на поверхности радиатора, а также конвективной теплопередачей и излучением с поверхности. Таким образом,
.=1/(1/(K +Л)+П/λП),
где а к, а л — коэффициенты теплопередачи конвекцией и излучением; λп — коэффициент теплопроводности покрытия; δп — толщина
покрытия.

Коэффициент эффективности ребра
характеризует температурный перепад по
высоте ребра h(рис. 5.35):
Kp = th(mh)/(mh),
где т =![]() Va U/KF — параметр, характеризующий форму ребра (α =αк + α л , U
Va U/KF — параметр, характеризующий форму ребра (α =αк + α л , U
— периметр сечения ребра, λ — коэффициент теплопроводности материала ребра, F —площадь поперечного сечения ребра).
Если на поверхности нет оребрения,
то коэффициент эффективности ребра
Рис. 5.35. Ребристый радиатор
воздушного охлаждения
Конвективный коэффициент тепло-
передачи a K определяется по критери-
218
алышм уравнениям (5.4) и (5.5). При этом характерный размер конст-
рукции радиатора L=b/2 , где b — расстояние между ребрами.
Для пластинчатого радиатора с вертикально ориентированными ре-
брами критерий Нуссельта рассчитывается по формулам:
Nu = 0,64+ 0,023GrL/D при 7≤GrL/D<20;
Nu = 0,5(GrL/D) при GrL/D≥20,
где D — длина ребра радиатора (см. рис. 5.35).
Коэффициент теплопередачи излучением αл находят по форму-
лам (5.33), (5.34) и (5.36).
Расчет радиаторов заключается в определении параметров конст-
рукции при заданном перегреве поверхности (проектный расчет) или в
определении перегрева поверхности при известных геометрических
размерах радиатора (поверочный расчет). Задача решается методом по-
следовательных приближений.
5.5. Тепловые режимы конструкций РЭС
с естественным воздушным охлаждением
Естественное воздушное охлаждение конструкций РЭС является
наиболее простым, надежным и дешевым способом охлаждения и осу-
ществляется без дополнительной затраты энергии. В конструкциях с
естественным воздушным охлаждением отсутствует конструктивная
избыточность, поскольку функции элементов системы охлаждения вы-
полняют элементы, образующие структуру конструкции. Однако эф-
фективность естественного воздушного охлаждения относительно
низка (см. табл. 5.7). Поэтому данный вид охлаждения может приме-
няться в конструкциях РЭС, работающих в облегченном тепловом ре-
жиме.
Передача тепла от конструкции окружающей среде осуществляется
конвекцией и излучением. Вывод тепла на корпус конструкции от внут-
ренних источников происходит за счет всех трех видов теплопередачи.
Различают две разновидности конструкций РЭС, в которых приме-
няется естественное воздушное охлаждение: конструкции с герметич-
ным для тепловых процессов кожухом и конструкции с перфорирован-
ным кожухом. Применительно к последним естественное воздушное
охлаждение называют естественной воздушной вентиляцией.
219
Процессы теплообмена конструкций с окружающей средой в значи-
тельной степени определяются их структурой. Поэтому все существую-
щие конструкции РЭС можно разделить на классы, для каждого из ко-
торых характерна тепловая модель и набор показателей, необходимых
для оценки теплового режима. Одним из признаков классификации мо-
жет служить структура нагретой зоны конструкции (расположение в
конструкции источников тепла). На основе этого признака произведена
классификация рассмотренных ниже конструкций РЭС.
5.5.1. Тепловое моделирование и расчет теплового режима
конструкций РЭС с источниками тепла, распределенными в объеме
К данному классу конструкций РЭС относятся конструкции блоков
книжного, веерного и разъемного типов. Общим для них является то,
что нагретая зона представляет собой объем, занимаемый собранными
в блок функциональными ячейками (ФЯ). Самая «горячая» точка кон-
струкций — центр нагретой зоны.
Схематическое изображение конструкции приведено на рис. 5.36, а.
Блок функциональных ячеек (нагретая зона) 1 размещен в корпусе 2 и
закреплен на корпусе с помощью установочных элементов (бобышек,
втулок, кронштейнов, угольников и др.) 3.

Рис. 5.36. Тепловая модель конструкции блока с объемной нагретой зоной:
а — схемотехническое изображение конструкции; б — тепловая схема
При построении тепловой модели принимаются следующие допу-
щения:
нагретая зона является однородным анизотропным телом;
источники тепла в нагретой зоне распределены равномерно;
поверхности нагретой зоны и корпуса — изотермические со средне-
поверхностными температурами t3, tк вн, tкн соответственно.
Тепло от центра нагретой зоны с температурой t30 теплопроводностью (эквивалентная тепловая проводимость σ3) выводится на поверхность нагретой зоны.
220
С поверхности нагретой зоны посредством конвективной (σЗК) и
лучевой (σЗЛ3) теплопередачи через воздушные прослойки, теплопроводностью контакта «нагретая зона — установочные элементы» (σтк)и самих установочных элементов (σЗ.Г) тепло передается на внутреннюю поверхность корпуса. За счет теплопроводности стенок (σ с к )тепло выводится на наружную поверхность корпуса,откуда конвекцией(α к к ) и излучением (αк л) переносится в окружающее пространство.
Тепловая схема, отражающая процесс теплообмена в конструкции, при-
ведена на рис. 5.36,6. Критериальной оценкой теплового режима конст-
рукций является температура в центре нагретой зоны t З.О. Как следует из тепловой схемы рис. 5.36, б,
tК.ВН.= tК.Н +P/σC.K.
tК.Н =tC+P/(σK.K+σК.Л.)
Здесь Р — тепловой поток, рассеиваемый конструкцией;
σ3 — тепловая проводимость нагретой зоны от центра к ее поверх-
ности:
где λz — эквивалентный коэффициент теплопроводности нагретой зо-
ны по направлению z; lx, ly, lz — приведенные геометрические раз-
меры нагретой зоны по соответствующим направлениям осей коорди-
нат; С — коэффициент формы нагретой зоны, определяемый по графи-
кам рис. 5.16;
σ 3 к — конвективно-кондуктивная тепловая проводимость между
нагретой зоной и внутренней стенкой корпуса:
где к п — поправочный коэффициент на конвективный теплообмен в
условиях ограниченного пространства; λ, В — коэффициент теплопро-
221
водности воздуха для среднего значения температуры воздуха в про-
слойке; lСР — среднее расстояние между нагретой зоной и кожухом;
S 3 — площадь поверхности нагретой зоны; S к вн — площадь внутрен-
ней поверхности корпуса;
σ 3 л — тепловая проводимость теплопередачи от нагретой зоны к
внутренней стенке корпуса излучением:
где α л — коэффициент теплопередачи излучением; σ т к — тепловая
проводимость контакта между нагретой зоной и установочными эле-
ментами;
σ 3 т— тепловая проводимость установочных элементов:
где п — число элементов; λ — коэффициент теплопроводности мате-
риала; l— длина установочных элементов по направлению теплового
потока; SCP — площадь средней изотермической поверхности, перпен-
дикулярной направлению теплового потока;
σ с к — тепловая проводимость стенок кожуха;
где λ с к— коэффициент теплопроводности материала корпуса; δ с к—
толщина стенки; S к вн, S к н — площади внутренней и наружной повер-
хностей корпуса;
σкк— тепловая проводимость от наружной поверхности корпуса к
среде для конвективной теплопередачи:
σк.к = αкSк.н
где α к — коэффициент теплопередачи; σкл=αлSкн — тепловая про-
водимость от наружной стенки корпуса к среде для теплопередачи из-
лучением; α л — коэффициент теплопередачи излучением.
Расчет показателей теплового режима блоков может быть выполнен
методом последовательных приближений или тепловой характеристи-
ки. В ориентировочных расчетах для определения тепловой проводи-
мости ст 3 от центра нагретой зоны к ее поверхности можно воспользо-
ваться [20] усредненными значениями эквивалентных коэффициентов
222
теплопроводности нагретой зоны: λ.х = λ,z = 0,35 Вт/(м • К),
λY, =0,09 Вт/(м • К). Оси координат Ох и Oz лежат в плоскости плат
функциональных ячеек, ось Оу — перпендикулярна плоскостям плат.
Для условий теплообмена в ограниченном пространстве коэффици-
ент теплопередачи излучением αлз может быть принят равным
7 Вт/(м2-К).
Порядок расчета тепловой контактной проводимости σ тк изложен в
разд. 5.4.1.
При малой толщине стенки (δ с к = 1,5...2 мм) тепловым сопротивлением стенок корпуса, выполненного из металлических сплавов с высоким коэффициентом теплопроводности, обычно пренебрегают. Однако если используется корпус из пластмассы, то тепловую проводимость стенок σ с к необходимо учитывать.
Для определения конвективного α к и лучевого αл коэффициентов
теплопередачи в условиях неограниченного пространства (теплообмен
между наружной стенкой кожуха и окружающей средой) можно вос-
пользоваться номограммами рис. 5.9 и 5.10.
5.5.2. Расчет собственного и наведенного перегрева
Перегрев любой точки или области конструкции является результа-
том взаимодействия источников тепла. Он складывается из собственно-
го и наведенного перегревов. Собственный перегрев определяется дей-
ствием источника тепла, расположенного в j-й точке при условии, что
остальные источники выключены. Наведенный перегрев обусловлен
действием всех источников тепла, кроме расположенного в j-й точке.
Для расчета собственного и наведенного перегревов тепловая мо-
дель должна быть детализирована до выделения отдельных источни-
ков тепла или групп источников. Решение задачи иллюстрируется на
примере блока разъемного типа, когда каждая функциональная ячейка
рассматривается как нагретая зона с распределенными в ней источни-
ками тепла. Данная модель позволяет рассчитывать собственный и на-
веденный перегревы функциональных ячеек и получать распределение
температуры внутри нагретой зоны блока.
Схематическое изображение конструкции блока приведено на
рис. 5.37.
В металлическом корпусе 1 размещено m функциональных ячеек,
собранных на корпусированных ИС. Каждая ячейка представляет собой
нагретую зону. Поверхности всех т нагретых зон — изотермические с
223

той зоны h3i = Ki3b + δП , где Ki3 —
коэффициент заполнения i-й функ-
циональной ячейки; b — шаг размещения ячеек в блоке; δп — толщина печатной платы.
Из-за малых воздушных зазоров
теплообмен между функциональны-
ми ячейками (2...3 мм) можно рас-
сматривать как процесс передачи
тепла теплопроводностью через ог-
раниченную многослойную стенку.
Рис. 5.37. Схемотехническое
изображение блока кассетной
конструкции
От плат функциональных ячеек ккорпусу и от корпуса к окружающей среде тепло передается конвекцией и излучением. Поверхности корпуса и функциональных ячеек (нагретых зон) принимают за изотермические со среднеповерхностными
температурами tK и t3i . Кроме того, считают, что функциональные
ячейки однотипны по конструкции, коэффициенты заполнения всех
плат одинаковы, воздушный зазор между ячейками b1 , =b -h3i постоя-
нен по всей площади платы.
Перегрев поверхности каждой ячейки складывается из собственно-
го перегрева Δ t., обусловленного действием только собственных источников тепла Р i и наведенного Δ tf H в результате действия источников тепла всех ФЯ, кроме i-й.
Тепловые схемы блока для расчета собственного и наведенного пе-
регревов приведены на рис. 5.38 и 5.39 соответственно. На схемах приняты следующие обозначения: t c — температура окружающей среды; Δ t к — перегрев корпуса блока; t3,-, Δ13,- — среднеповерхностная температура и перегрев i-й функциональной ячейки; R σ0 — тепловое сопротивление воздушной прослойки между крайними ячейками и кожухом; R σ — тепловое сопротивление между соседними ячейками; R B тепловое сопротивление воздушных прослоек между торцевыми поверхностями ФЯ и кожухом.
Предполагается, что тепловой поток Р i рассеиваемый нагретой зо-
ной i-й ФЯ, распространяется влево и вправо от ячейки.
При этом часть теплового потока, идущая в левую сторону, Рiл об-
ратно пропорциональна тепловому сопротивлению левой от i-й функ-
циональной ячейки ветви Рiл. Составляющая теплового потока, рас-
224

Рис. 5.38. Тепловая схема блока для расчета собственного перегрева:
а — исходная схема; б — преобразованная
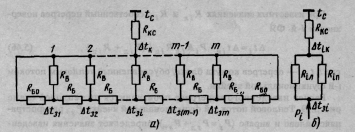
Рис. 5.39. Тепловая схема блока для расчета наведенного перегрева
пространяющаяся в правую сторону, Рiп обратно пропорциональна
тепловому сопротивлению правой ветви Рiп (рис. 5.38, б).
Как следует из тепловой схемы рис. 5.38, а,
Riл =[ R(i-1)л(Rв + Rσ)+RвRσ]/(R(i-1)л + Rв). (5.44)
R i.п = [(Rб+R(i+1)п)Rв]/(Rв+Rб+R(i + 1)П), (5.45)
гдеR1л = Rб0, i=l, 2 т.
225
При известных значениях R i л и R iп собственный перегрев поверхности i-й ФЯ
Δti,. = Δtik + PiRiл.Riп/(Riл+ Riп) (5-46)
где Δ t {к — перегрев кожуха блока, обусловленный тепловым потоком
1-й функциональной ячейки.
Расчет наведенного перегрева производится по тепловой схеме
рис. 5.39. Тепловой поток s-й функциональной ячейки РS , распространяясь влево и вправо (РS=PSJ1 + Psn), определяет значения наведенных на соседних ячейках перегревов. Из схемы рис. 5.39
PSJ1=(ΔtS - ΔtSK)/RSЛ (5-47)
PSП=(ΔtS - ΔtK)/RSП (5.48)
Входящие в (5.47) и (5.48) тепловые сопротивления PSJ1и PSП рас-
считываются по формулам (5.44) и (5.45), собственный перегрев s-й
ячейки Δ ts — по формуле (5.46).
Перегревы, наведенные на функциональные ячейки, расположен-
ные слева от s-й, определяются соотношениями:
ΔtS(S-1)=ΔtS-PSЛRσ;P*(S-1)Л=(ΔtS(S-1)-ΔtSK)/RB
P(S-1)Л=PSЛ- P*(S-1)Л; ΔtS(S-2)= ΔtS(S-1)- P(S-1)ЛRσ;…
…;P*2Л= (ΔtS2-ΔtSK)/RB; P2Л = P3Л-P*2Л ; ΔtS1= ΔtS2-P2ЛRσ
Перегревы, наведенные на ФЯ, расположенные справа:
P*SП=(ΔtS-ΔtSK)/RB;P(S+1)П= PSП- P*SП;
ΔtS(S+1)=ΔtS-P(S+1)ПRσ; P*(S+1)П=(ΔtS(S+1)-ΔtSK)/RB
P(S+2)П= P(S+1)П-P*(S+1)П;…;PmП= P(m-1)П- P*(m-1)П
ΔtSm= ΔtS(m-1)-PmПRσ
226
Перегрев поверхности i-й функциональной ячейки с учетом собст-
венного и наведенного перегревов согласно принципу суперпозиции
можно найти как
Тепловое сопротивление R 6 0 обусловлено конвективно-кондуктивной и лучевой теплопередачами через воадушную прослойку между
боковой поверхностью крайней платы и внутренней боковой стенкой
кожуха:
RбО=Δy/(кпλBScр + αЛSПЛΔу),
где Δ у — толщина воздушной прослойки; к п — поправочный коэффициент на конвективную теплопередачу; λв — коэффициент теплопроводности воздуха; Sср = 0,5(Sпл + Sстб) — площадь средней изотермической поверхности; S ПЛ = lплxlпyx — площадь поверхности платы ФЯ; 1ПЛХ, /ПЛ2 — геометрические размеры платы; S стб— площадь внутренней боковой стенки кожуха; α л — коэффициент теплопередачи излучением.
Тепловое сопротивление R B характеризует конвективно-кондуктив-
ную и лучевую теплопередачи между торцевой поверхностью функци-
ональной ячейки и внутренней поверхностью кожуха, охватывающей
торцевые поверхности ФЯ (нагретых зон):
Rв = ΔX/(кпλвSср + αлSiтΔх),
где Δx — средняя толщина воздушной прослойки между торцевой поверхностью нагретых зон и внутренней поверхностью кожуха; SCP =
= 0,5(SiT + SКВН) — площадь средней изотермической поверхности;
SiT = 2 h 3i(lплх +lплz) — площадь торцевой поверхности i-й нагретой
зоны; S к вн— площадь внутренней поверхности кожуха, охватывающей
торцевые поверхности нагретых зон.
Тепловое сопротивление между соседними платами R σ = b/λуSпл,где λy, — эквивалентный коэффициент теплопроводности нагретой зоны блока по направлению y- Определение λy, производится в результа-
227
те моделирования нагретой зоны блока, состоящей из m функциональ-
ных ячеек, однородным анизотропным телом.
5.5.3. Тепловое моделирование и расчет теплового режима блоков
цифровых РЭС на микросборках
Блоки цифровых РЭС на микросборках обычно выполняются в виде
конструкций книжного типа (см. рис. 3.10). Нагретая зона микроблока
состоит из функциональных ячеек на металлических рамках, выполня-
ющих функции несущих элементов конструкции и кондуктивных теп-
лостоков.
Процессы теплообмена можно представить тепловой моделью кон-
струкций с источниками тепла, распределенными в объеме (см. разд.
5.5.1).
Однако при определении тепловой проводимости между центром и
поверхностью нагретой зоны а 3 в конструкции ФЯ (рис. 5.40) свойство
«дальнего порядка» частично нарушается, поскольку не все элементы
конструкции имеют одинаковые геометрические формы и не выполня-
ется требование периодичности их размещения. Поэтому параметры
модели нагретой зоны в виде однородного анизотропного тела получа-
ют на основе выбора в качестве элементарной тепловой ячейки функ-
циональной ячейки микроблока (системы с «ближним порядком).

Рис. 5.40. Конструкция односторонней функциональной ячейки
Как видно из рис. 5.40, тепло по направлению х в конструкции ФЯ
передается преимущественно через боковые ребра жесткости рамки 1 и
228
печатную плату 3. Другие элементы конструкции, обладающие отно-
сительно высокими коэффициентами теплопроводности, включены
последовательно с воздушными прослойками (λ в = 0,025 Вт/(м • К)).
Аналогичен механизм передачи тепла через элементы конструкции
ФЯ в направлении у. Основными цепями переноса тепла являются вер-
хнее 2 и нижнее 4 ребра жесткости рамки.
По направлению z тепло в пределах ФЯ передается через винты,
стягивающие ячейки в пакет, и через ребра жесткости рамки 1 и 2, по
которым осуществляется тепловой контакт между ячейками в пакете.
Таким образом, тепловые проводимости ФЯ по направлениям осей
координат:
σЯХ=2λPSP1/lP1; σЯY=λP(SP3+SP4)/lP3
σЯZ=λBHSBH+λPSKH.P)/lBH
где λP — коэффициент теплопроводности материала рамки; Sp1,
Sp2 Sp3 — площади поперечного сечения соответствующих ребер
жесткости рамки; lp1, lp3 — длины ребер жесткости; λ, вн — коэффициент теплопроводности материала стягивающих винтов; S вн — суммарная площадь поперечного сечения винтов; SКН— площадь теплово-
го контакта между рамками ФЯ; l вн — длина винта в пределах рамки
или высота рамки.
Тепловые проводимости нагретой зоны по направлениям осей коор-
динат
σзx=mσЯХ , σзy=mσЯY , σзz=σЯZ/m
где m— число функциональных ячеек в блоке.
Эквивалентные коэффициенты теплопроводности нагретой зоны по
направлениям координат:
lX = σ3XlX /lylz'> λy = σ3y ly / lxlz> λz = σz lz / lXly
где lx, ly , lz — геометрические размеры нагретой зоны по направлениям координат.
Эквивалентные размеры нагретой зоны для λ z = λ0, lz0 = l z:
229
Через отношения lz/lxo и lz/ly0 по графикам рис. 5.16 находят
коэффициент формы нагретой зоны С, после чего определяют тепло-
вую проводимость между центром и поверхностью нагретой зоны:
σ3 = 4λzlxly/Clz.
5.5.4. Тепловое моделирование и расчет теплового режима
конструкций РЭС с источниками тепла,
расположенными в плоскости
Модель распространяется на конструкции блоков и модулей РЭС,
выполненных на одной плате, закрепленной на кожухе.
Упрощенное изображение конструкции приведено на рис. 5.41, а,
тепловая схема — на рис. 5.41, б. Особенностью таких конструкций яв-
ляется распределение источников тепла в одной плоскости. Механизм
теплообмена и тепловая модель в целом аналогичны конструкциям
РЭС с источниками тепла, распределенными в объеме (см. рис. 5.36, а).
Однако размещение тепловыделяющих элементов в плоскости дает

Рис. 5. 41. Тепловая модель конструкции блока с пленарной нагретой зоной:
а — упрощенное изображение конструкции; б — тепловая схема
возможность при оценке теплового режима ограничиваться расчетом
среднеповерхностной температуры нагретой зоны t3, которая с неболь-
шой погрешностью может быть принята в качестве характеристики теп-
лового режима элементов. Структуры тепловых проводимостей на теп-
ловых схемах рис. 5.36, б и 5.41, б полностью совпадают.
5.5.5. Тепловое моделирование и расчет теплового режима
конструкций РЭС с естественной вентиляцией
Естественная вентиляция в конструкциях осуществляется за счет
перфорации кожухов, что обеспечивает естественное подтекание холодного воздуха к тепловыделяющим элементам и, тем самым, повышает эффективность теплообмена.
Интенсивность свободной конвекции с притоком воздуха извне ха-
рактеризуется коэффициентом перфорации
230
KП=SBX/(L1 L2)
где Sвх — суммарная площадь отверстий в нижней стенке кожуха на
входе в блок; L 1, L 2 — геометрические размеры стенки.
Обычно коэффициент перфорации Кп = 0,05...0,1. Входные и вы-
ходные отверстия в кожухе выполняются напротив нагретой зоны плат,
причем суммарная площадь выходных отверстий в 1,5—2 раза больше
SBX
Показатели теплового режима блока с перфорированным кожухом
могут быть найдены, если известны показатели для блока с естествен-
ным воздушным охлаждением без притока воздуха:
ΔtзОЕВ = СпΔtзО; Δtз.ЕВ = СпΔtз; Δtк.ЕВ = Сп Δtк

Δt зОЕВ , ΔtзО , Δtз.ЕВ , Δtз , Δtк.ЕВ , tк— перегревы центра
нагретой зоны, поверхности нагретой зоны и поверхности кожуха для конструкций с перфорированным (ЕВ) и
глухим кожухом; С п — поправочный
коэффициент, являющийся функ-
цией коэффициента перфорации.
График зависимости С п от коэф-
фициента перфорации Кп приведен
на рис. 5.42.
Рис. 5.42. График для определения
поправочного коэффициента С „
Таким образом, конструкции бло-
ков с естественной вентиляцией мож-
но представить тепловыми моделями
блоков с глухими кожухами и после
расчета показателей теплового режима ввести поправку на естественную вентиляцию.
5.5.6. Тепловое моделирование конструкций с тепловыделяющими
элементами, размещенными на металлических основаниях
Данный класс объединяет конструкции аналоговых МЭА на микро-
сборках. Типичный представитель — конструкции в корпусах типа «пе-
нал». Упрощенное изображение конструкции приведено на рис. 5.43, а.
Бескорпусные микросборки 3 размещены на металлическом основа-
нии 2, которое устанавливается в корпус 1. Характерная особенность
конструкций — передача тепла от элементов микросборок к корпусу
преимущественно теплопроводностью через внутреннюю тепловую
231
проводимость тепловыделяющих элементов σвн, тепловые проводимости подложки микросборки σ п и клеевого соединения σКЛ подложки
микросборки и основания. Основание и корпус можно принять за изо-
термическую поверхность. Передача тепла с поверхности корпуса ок-
ружающей среде осуществляется конвекцией и излучением. При усло-
вии, что в пределах каждой из п микросборок отсутствует взаимное
тепловое влияние между элементами (предусмотрены зоны тепловой
защиты элементов) тепловая схема процесса теплообмена в конструк-
ции может быть представлена в виде рис. 5.43,6.

Рис. 5.43. Тепловая модель конструкции пенального типа на микросборках:
а — схематическое изображение конструкции; б — тепловая схема

















