- (x ∨ y) ⊕ z ⊕ 0
- ¬(¬x ∨ y) ∨ (¬y ∨ z)
- ¬(¬x ∧ z) ∧ x ∧ ¬y
- (x ∧ y ∧ z) ⊕ (x ∧ y) ⊕ 0
- ¬(x ∨ (¬x ∨ ¬y)
- x ∧ ¬(y ∨ z) ∧ (x ∨ y)
- x ∧ (y ∨ z) ∧ (x ∨ y)
- ¬(x ∧ y ∧ ¬z) ∧ (¬x ∧ ¬z)
- x ∨ ¬(¬y ∨ z) ∨ y
- (x ∧ y) ⊕ z ⊕ 1
Дискретная математика - ответы на вопросы на СтудИзбе
- Логическая операция, изменяющая истинность значения логической переменной
- Операция, связывающая два простых логических выражения, и содержащая конструкцию «ЕСЛИ - ТО»
- Операция над парой высказываний, результат которой истинен только когда истинны оба высказывания
- Операция над парой высказываний, результат которой является ложным только когда ложны оба высказывания
- Операция над парой высказываний, результат которой является истинным если оба высказывания одновременно истинны или ложны и ложным в любом другом случае
- Симметричность
- Транзитивность
- Рефлексивность
- Антисимметричность
- ((x → y) → ((x → ¬z) → (y → ¬z)))
- ((x → y) → ((¬y → ¬z) → (¬x → ¬z)))
- ((¬x → y) → ((y → z) → (¬x → z)))
- ((¬x → ¬y) → ((¬x → (¬y → z)) → (¬x → z)))
- P
- Q
- R
- Все
- Ни одно
(ответ введите в именительном падеже прописными буквами)
мальчика не должны стоять рядом
(в качестве ответа введите число без пробелов)
- совершенная дизъюнктивная нормальная форма
- полином Жегалкина
- совершенная конъюнктивная нормальная форма
- полиномиальная форма
- элементарное произведение
F: f = X ∧ Y ∧ ¬Z, g = X ∨ Y , h = X ⊕ Y ⊕ 1
- никакую
- g
- f
- h

- двоичная
- булева
- двойственная
- самодвойственная
- переключательная
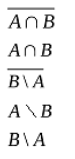
- Да
- Нет

- (x ∨ y) ∧ (¬x ∨¬y∨ z)
- (x ∨ y) ∧ (¬y ∨ ¬z)
- (x ∨¬y) ∧ (¬x ∨¬y∨ z)
- x ∧ ¬y ∧ (x∨ z)
- y ∧ (¬x ∨ z) ∧ (x ∨ y ∨ z)




- множество, полученное объединением счётного числа счётных множеств
- Множество иррациональных чисел интервала (1, 2)
- множество всех пар рациональных чисел
- множество всех окружностей на плоскости
- Множество точек разрыва монотонно убывающей на [а, b] функции
- ((¬X ∧ Z) → (Y ∧ ¬Z)) ∧ Y
- (X ∨ Y) ⊕ (Y ∧ Z) ⊕ (X ∧ Y ∧ Z)
- (Y → ¬X) → (Y ∧ Z)
- НИ ОДНА
- (р → q) ↔ ¬p
- (р → q) ↔ (¬q → ¬p)
- (р → ¬q) ↔ pq
- (A B) C = A (B C)
- (A B) ∪ (A C) = A (B ∩ C)
- (A B) ∪ (A C) = A (B ∪ C)
- A ∩ (B C) = (A ∩ B) C

- p → ¬p = 1
- ¬p → q = p v q
- p → p = 1
- p → 1 = 1
- p → 0 = ¬p
Укажите, какие из следующих формул задают нелинейные функции
(X ∧ Y) ∨ (¬X ∧ ¬Y)
(Y ∧ ¬X) → Z
¬Z ∨ X ∨ Y
НИ ОДНА
- (р → q) ↔ (¬q → ¬p)
- (р → ¬q) ↔ pq
- (р → q) ↔ ¬p
(ответ введите прописными буквами)
Чему равно множество
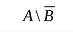
- [1,2,3]
- [0,1,6,7,8,9]
- [2,3,4,5]
- (1
- [2,3]
- (X → ¬Y) ∨ (¬X ∧ ¬Y)
- (X ∨ Y) → ¬Z
- (Y ∧ ¬X) → (Z → X)
- НИ ОДНА
(ответ введите в именительном падеже прописными буквами)
- (X ∧ Y ∧ Z) ∨ (¬ X ∧ ¬Y ) ∨ (X ∧ Y ∧ ¬ Z)
- (Y → ¬X) → Z
- (Z→ X) ∨ Y
- НИ ОДНА
- Гамильтона
- Дейкстры
- Краскала
- Прима
- Эйлера
Укажите, какие из следующих формул задают несамодвойственные функции
(X ∧ ¬Z) ∨ (Y ∧ ¬Z) ∨ ( X ∧ Y)
(¬ X ∧ Y) ∨ (Z ∧ ¬(X ⊕ Y))
X ∨ (¬ Y ∧ Z)
НИ ОДНА
(в качестве ответа введите число)
- ¬Z ∨ X ∨ Y
- (X → ¬Y) ∨ (¬X ∧ ¬Y)
- НИ ОДНА
- (Y ∧ ¬X) → (Z → X)
- {0, 1, 2}
- {0, {4}}
- {0, {{5}}}
- {4, {3}, 0}
- {{0, 1, 2}, {5}}
- {{3}, 4, {{5}}, 6}
- хfу <=> х > у
- хfу <=> х + у - четно
- хfу <=> х - делитель у
- хfу <=> х = у
- хfу <=> х делится на у
- провести дифференцирование
- провести интегрирование
- разрешить уравнение относительно n-го члена

Чему равно множество

- [0,6,7,8,9]
- [1,2,3,4,5]
- [6,7,8,9,]
- [0,1,2,3,4,5]
- {0,2,3,4,5,6,7,8,9]
- (y ∧ ¬z) ∨ (¬x ∧ ¬z)
- (y ∧ ¬z) ∨ ¬((¬x ∧ ¬z))
- ¬((y ∧ ¬z) ∨ (¬x ∧ ¬z))
- ¬(y ∧ z) ∨ (¬x ∧ ¬z)
- ¬(y ∨ z) ∧ (¬x ∨ ¬z)
(в качестве ответа введите число)
- (p +q)+>(-q+-p)
- (p+q)+>-p
- (p+-q)+pq
(ответ введите в винительном падеже прописными буквами)
- (x ∧ y ∧ ¬z) ∨ (¬x ∧ ¬z)
- (x ∨ y ∧ ¬z) ∨ (¬x ∧ ¬z)
- ¬((x ∧ y) ∧ ¬z) ∨ (¬x ∧ ¬z)
- ¬(x ∧ y) ∨ x
- ¬(x ∨ y) ∧ x
- умножение чисел
- симметрическая разность множеств
- вычитание чисел
- пересечение множеств
- разность множеств
- инъективность
- всюду определенность
- функциональность
- сюръективность
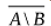
- {0,1,2,3,4,5}
- {0,2,3,4,5,6,7,8,9}
- {0,6,7,8,9}
- {1,2,3,4,5}
- {6,7,8,9,}
Пусть заданы множества A = {0, 1, 2, 3}, B = {1, 2, 4}, C = {a, b, c} и D = {b, d, e}. Чему равно множество F = (A B) × (C D)
{(0, a), (0, c), (2, a), (2, c)}
{(0,a), (0,c), (3, a), (3,c)}
{(0,b), (0, c), (3, b), (3,c)}
{(1, a), (1, c), (2, b), (2,c)}
{0, 3, a, c}
- R
- P
- Q
- Все
- Ни одно
- p ⊕ 0 = p
- p ⊕ 1 = ¬p
- p ⊕ q ⊕ pq = p v q
- p ⊕ p = 1
- (y ∨ z) ∧ (¬x ∨ ¬z)
- (y ∨ ¬z) ∧ (¬x ∨ ¬(¬z ∨ y))
- (y ∨ ¬z) ∧ ¬(¬x ∨ ¬z)
- (¬(x ∨ y) ∨ ¬z) ∧ (¬x ∨ ¬z)
- ¬(y ∨ ¬z) ∧ (¬x ∨ ¬z)
- ((¬x → y) → ((y → ¬z) → (¬x → ¬z)))
- ((¬x → ¬y) → ((¬x) → ¬x))
- ((¬x → ¬y) → ((¬x → (¬y → z)) → (¬x → z)))
- ((x → y) → ((¬y → ¬z) → (¬x → ¬z)))
- биекция
- взаимно-однозначное
- отображение "в"
- отображение "на"
- функция
Подграф, множество вершин которого совпадает с множеством вершин самого графа, называется ...
Укажите, какие из следующих формул задают несамодвойственные функции
(X ∧ ¬Z) ∨ (Y ∧ ¬Z) ∨ (X ∧ Y)
X ∨ (Y ∧ ¬Z)
X ⊕ Z ⊕ (Y ∧ Z)
НИ ОДНА
- {(0, a), (0, c), (0,e), (1, a), (1, b), (1,e)}
- {(0,a), (0, c), (1,a), (1,c)}
- {(0,a), (0,b), (0, c), (1, a), (1, b), (1,c)}
- {(0,a), (0,c), (1,a), (1,c), (2,a), (2,c)}
- {0, 1, a, c}
по крайней мере одним элементом или порядком их следования, называются:
- размещения
- сочетания
- перестановки
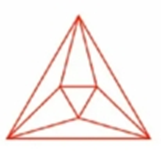
- 1
![]()
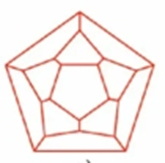
- 2
![]()
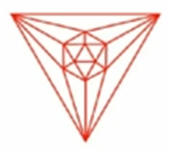
- 3
![]()
F: f=XvY,g=X+-Y, h=XOY
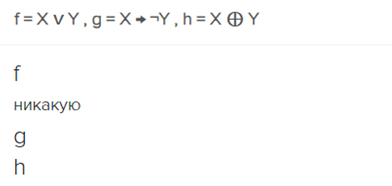
- f
- никакую
- g
- h
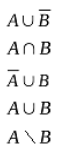
- обладает эйлеровым циклом
- не обладает эйлеровым циклом
- может обладать эйлеровым циклом – это зависит от числа дуг
Какая из следующих конъюнктивных нормальных форм эквивалентна формуле: (x ∨ y) → (x ∧¬y ∧ z)
(x ∨ y ∨ z) ∧ (¬y ∨ z)
(¬x ∨¬y) ∧ (¬x ∨ z)
¬y ∧ (x∨ z)
¬y ∧ (¬x ∨ z)
¬y ∧ (¬x ∨¬y)
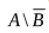
- {3}
- {2,3,4,5}
- {1,2,3}
- {0,1,6,7,8,9}
- {1}

- 1
- 2
- 3
- 4
- 5
- 6
- любое количество





Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Лично меня всё устраивает - и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
 meimei1337
meimei1337 iFate
iFate

 Анастасия Жукова
Анастасия Жукова

 EcoTime Inc.
EcoTime Inc.




























