Марковские процессы с дискретным временем
3. Марковские процессы с дискретным временем.
Как было определено ранее, для случайных процессов с дискретным временем изменения состояний возможны только в определенные моменты времени, и эти моменты обозначим через t0, t1, t2, … . В случае дискретной цепи Маркова для описания переходов между состояниями используются вероятности переходов, определяемые как
pij(tk)=Pr{g(tk+1)=Ej|g(tk)=Ei}, i,j=0,n.
Вероятность перехода (за один шаг) pij(tk) задет вероятность того, что случайный процесс на следующем (k+1)-ом шаге перехода (в момент времени tk+1) окажется в состоянии Ej при условии, что на текущем k-ом шаге (в момент времени tk) он находится в состоянии Ei.
Если вероятности переходов pij(tk) не зависят от момента времени tk, т.е. pij(tk)=pij, то цепь Маркова называется однородной, в противном случае - неоднородной. Далее будем рассматривать только однородные цепи Маркова.
Вероятности переходов pij, i,j=0,n, обычно задаются в виде квадратной матрицы T размерности (n+1)´(n+1):
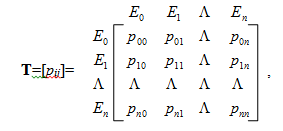
элементы которой удовлетворяются условиям:
, i=0,n;
Рекомендуемые материалы
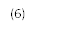
, i,j=0,n.
Условие (5) означает, что в любой момент времени t0, t1, t2, … процесс обязательно (с вероятностью 1) перейдет из состояния Ei в какое-либо другое состояние E0, E1,×××, En, причем не исключается возможность перехода в то же самое состояние.
Матрица, удовлетворяющая условиям (5) и (6), называется стохастической. Поскольку элементами стохастической матрицы Т являются вероятности переходов pij, то эта матрица называется матрицей вероятностей переходов.
Наряду с вероятностями переходов pij за один шаг, определим вероятности переходов за m шагов в виде
, m=1, 2, …
Здесь 
задет вероятность того, что через m переходов случайный процесс окажется в состоянии Ej при условии, что на текущем шаге он находится в состоянии Ei. В силу однородности марковской цепи вероятности , i,j=0,n, не зависят от текущего времени tk.
Используя марковское свойство, легко вывести следующую формулу для вычисления вероятностей :
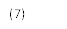
, m=2, 3, …
Это равенство означает, что для попадания из состояния Ei в состояние Ej за m шагов необходимо сначала попасть из состояния Ei в некоторое состояние Ek за m-1 шагов, а затем за один шаг перейти из Ek в Ej. Вероятность этих двух независимых событий (они независимы в силу марковского свойства) равна произведению вероятностей каждого из них, и, если просуммировать эти произведения по всем возможным промежуточным состояниям Ek, то получится вероятность .
Цепь Маркова называется неприводимой, если каждое ее состояние может быть достигнуто из любого другого состояния, т.е. для каждой пары состояний Ei и Ej существует целое число m0 такое, что 
. Состояние Ei называется поглощающим, если процесс достигнув это состояние, не покидает его. Очевидно, для поглощающего состояния pii=1. Состояние Ei называется невозвратным, если случайный процесс после какого-то числа переходов непременно покидает его.
Вернемся к вопросу определения вероятностей состояний Pi(tk), i=0,n, предполагая, что начальные вероятности Pi(t0), i=0,n, при t0=0 известны.
Используя доводы, аналогичные тем, что были приведены для обоснования равенства (7), легко определить, что искомые вероятности после первого шага, т.е. на момент времени t1
, i=0,n.
Вероятности состояний после второго шага на момент времени t2 определяются аналогично:
, i=0,n.
В общем случае после k-го шага на момент времени tk, k=1, 2,..., вероятности состояний будут равны
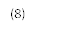
, i=0,n.
В векторной форме равенства (8) имеют вид:
P(tk)=P(tk-1)T.
Если случайный процесс обладает эргодическим свойством, т.е. существуют пределы 
, i=0,n, то соответствующие предельные значения вероятностей состояний Pi, i=0,n, для стационарного режима определяются из решения системы уравнений:
, i=0,n
или в векторном виде
P=PT
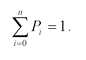
с нормировочным условием
В системе (10) уравнения являются линейно зависимыми и любое из них можно исключить из нее, а недостающее при этом (для однозначного определения n+1 неизвестных) уравнение составляет условие (11).
Сформулируем теперь правило составления уравнений для стационарных вероятностей состояний марковского процесса с дискретным временем по графу переходов. Для каждого состояния уравнение составляется следующим образом. В левой части уравнения записывается стационарная вероятность рассматриваемого состояния. Правая часть представляет собой сумму членов, число которых равно числу дуг, входящих в рассматриваемое состояние. Каждый член представляет собой произведение вероятности перехода, соответствующей данной дуге, на вероятность состояния, из которого исходит эта дуга. Сформулированное правило позволяет чисто механически записывать уравнения для стационарных вероятностей состояний непосредственно по графу переходов.
Пример. Рассмотрим систему, которая состоит из двух устройств y1 и y2, каждое из которых может находиться в одном из двух состояний: не работает (обозначим это состояние через 0) и работает (состояние 1). В определенные моменты времени может включиться или выключиться только одно устройство. Пусть процесс функционирования такой системы описывается процессом с дискретным временем. Выделим возможные состояния процесса (системы):
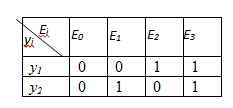
Предположим, что известны вероятности переходов, представленные в виде матрицы
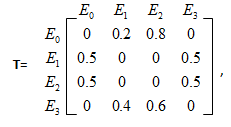
и начальные вероятности P0(0)=0,7, P1(0)=P2(0)=P3(0)=0,1. Граф переходов для этого процесса имеет вид, показанный на рис. 2.
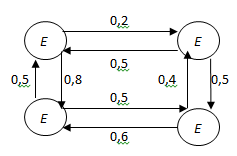
Рис. 2. Граф переходов.
Определим вероятности состояний на различные моменты времени. Согласно формуле (8) вероятности состояний на момент времени t1:
P0 (t1) =P0 (0) p00 + P1 (0) p10 +P2 (0) p20 + P3 (0) p30 =0.1;
P1 (t1) =P0 (0) p01 + P1 (0) p11 +P2 (0) p21 + P3 (0) p31 =0.18;
P2 (t1) =P0 (0) p02 + P1 (0) p12 +P2 (0) p22 + P3 (0) p32 =0.62;
P3 (t1) =P0 (0) p03+ P1 (0) p13 +P2 (0) p23 + P3 (0) p33 =0.1;
на момент времени t2:
P0 (t2) = P0 (t1) p00 + P1 (t1) p10 + P2 (t1) p20 + P3 (t1) p30 =0.4;
P1 (t2) = P0 (t1) p01 + P1 (t1) p11 + P2 (t1) p21 + P3 (t1) p31 =0.06;
P2 (t2) = P0 (t1) p02 + P1 (t1) p12 + P2 (t1) p22 + P3 (t1) p32 =0.14;
P3 (t2) = P0 (t1) p03 + P1 (t1) p13 + P2 (t1) p23 + P3 (t1) p33 =0.4;
и т.д.
Лекция "24.Тема любви в поэзии Бодлера" также может быть Вам полезна.
Предполагая, что рассматриваемый случайный процесс обладает эргодическим свойством, что соответствует действительности, определим вероятности состояний для стационарного режима. Искомые вероятности P0, P1, P2, P3 могут быть найдены, согласно равенствам (10) и (11), из системы уравнений:
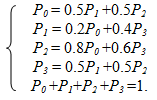
Легко проверить, что такую же систему мы получим, если воспользуемся приведенным выше правилом составления уравнений для стационарных вероятностей по графу переходов.
Решив систему уравнений, получим: P0 =0.25; P1 =0.15; P2 =0.35; P3 =0.25.
В заключении вернемся к вопросу о свойстве отсутствия последействия для марковских цепей с дискретным временем и докажем, что время пребывания в данном состоянии имеет геометрическое распределение.
Предположим, что процесс только что перешел в состояние Ei. Он останется в этом состоянии на следующем шаге с вероятностью pii и с вероятностью 1-pii уйдет из этого состояния. Если процесс действительно останется в этом состоянии, то вероятность того, что на следующем, втором, шаге он останется в данном состоянии, по-прежнему равна pii, а вероятность того, что процесс перейдет в другое состояние, останется равной 1-pii. И так далее. Более того, благодаря марковскому свойству тот факт, что процесс пребывал в данном состоянии известное число шагов, никак не сказывается на вероятности остаться на следующем шаге в этом же состоянии или перейти в некоторое другое состояние. Так как эти события независимы, то вероятность того, что процесс находился в состоянии Ei точно m шагов и затем сразу перешел в другое состояние, равна (1-pii)
, что и задает геометрическое распределение.
