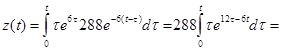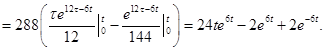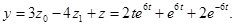Решение линейных дифференциальных уравнений методами операционного исчисления

§4. Решение линейных дифференциальных уравнений методами операционного исчисления. 

   Рассматривается задача Коши для линейного дифференциального уравнения  n – го порядка с постоянными коэффициентами и правой частью, удовлетворяющей всем условиям существования изображения:

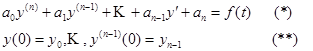
Самый непосредственный способ решения, использующий операционные методы, заключается в следующем: умножим уравнение (*) на    и проинтегрируем по переменной  t  от 0 до ∞. Обозначив изображения функций  y(t)  и  f(t)  через  Y(p)  и  F(p) , воспользуемся формулами изображения производных (§2, св.4) и начальными условиями (**). В результате получим:

  Из этого соотношения можно выразить  Y(p) и затем, используя либо формулу Меллина, либо свойства изображений и изображения известных функций, восстановить оригинал, т.е. решение уравнения (*) – (**). Ясно, что этим методом можно пользоваться только в самых простых случаях.

Пример.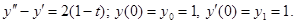

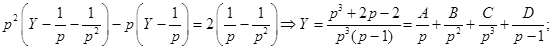
   Обычно, задача разбивается на две более простые: однородное уравнение с ненулевыми начальными условиями и неоднородное – с нулевыми. В силу линейности, сумма полученных решений будет решением задачи (*) – (**). Применим этот метод к задаче последнего примера.

Рекомендуемые материалы

 1)   

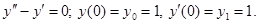
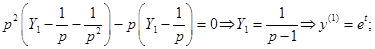
 2)

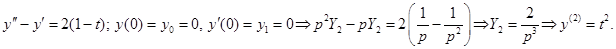
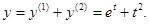
   Необходимо отметить, что после перехода в уравнении (*) к изображениям, коэффициент при функции Y(p) равен характеристическому многочлену  P_n(p). Это обстоятельство иногда используется при следующем методе решения.

   Решаются  n  однородных уравнений  (*)  (будем обозначать их решения через  z_j(t)) с начальными условиями  (символ Кронекера) . Решение однородного уравнения с начальными условиями  (**) будет равно: .

Легко видеть, что изображение  Z_n-1 определяется равенством . Все функции z_j(t)  находятся так же, как и раньше.

  При решении неоднородного уравнения с нулевыми начальными условиями получается равенство . Пользуясь теоремой о свертке, для решения неоднородного уравнения получим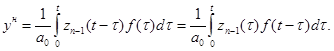

Пример.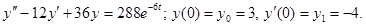

 I.  

1)  

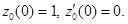
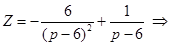
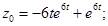
Вам также может быть полезна лекция "1.2 Типология культур и цивилизаций".

2)    

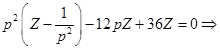
II.