Дифференцируемость функции комплексной переменной
Дифференцируемость функции комплексной переменной.
19.3.1. Определение производной. Аналитичность ФКП. Пусть  определена, однозначна и принимает собственные значения в окрестности точки
определена, однозначна и принимает собственные значения в окрестности точки  . Производной функции
. Производной функции  в точке
в точке  называется предел
называется предел  . Функция, имеющая конечную производную в точке
. Функция, имеющая конечную производную в точке  , называется дифференцируемой в этой точке.
, называется дифференцируемой в этой точке.
В этом определении важно, что стремление  может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной
может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной  не сводится к существованию частных производных функций
не сводится к существованию частных производных функций  и
и  , а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функции в точке и в области.
, а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функции в точке и в области.
Определение. Однозначная функция называется аналитической (регулярной, голоморфной) в точке  , если она дифференцируема в некоторой окрестности этой точки.
, если она дифференцируема в некоторой окрестности этой точки.
Однозначная функция называется аналитической в области D, если она аналитична в каждой точке этой области.
Примеры. 1.  . В этом случае
. В этом случае 
 . Таким образом , эта функция дифференцируема в любой точке, и её производная равна 2z.
. Таким образом , эта функция дифференцируема в любой точке, и её производная равна 2z.
2.  Докажем, что эта функция не имеет производной ни в какой точке
Докажем, что эта функция не имеет производной ни в какой точке  . Будем стремить
. Будем стремить  по двум путям: по прямой, параллельной действительной оси Ох (в этом случае
по двум путям: по прямой, параллельной действительной оси Ох (в этом случае  ), и по прямой, параллельной мнимой оси Оу (в этом случае
), и по прямой, параллельной мнимой оси Оу (в этом случае  ). В первом случае
). В первом случае  , во втором
, во втором 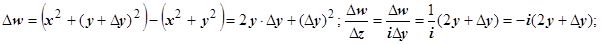
 . Эти пределы равны, только если
. Эти пределы равны, только если 
 . Таким образом, функция
. Таким образом, функция  может быть дифференцируема в единственной точке
может быть дифференцируема в единственной точке  , во всех остальных точках пределы
, во всех остальных точках пределы  различны в зависимости от способа стремления
различны в зависимости от способа стремления  , т.е.
, т.е.  не существует.
не существует.
19.3.2. Условия Коши-Римана (Даламбера-Эйлера).Сейчас мы сформулируем и докажем важнейшую в теории ФКП теорему о необходимых и достаточных условиях дифференцируемости (а, следовательно, аналитичности) функции.
Рекомендуемые материалы
Для того, чтобы функция  была дифференцируема в точке
была дифференцируема в точке  , необходимо и достаточно, чтобы функции
, необходимо и достаточно, чтобы функции  и
и  были дифференцируемы в точке (х,у), и чтобы в этой точке выполнялись соотношения
были дифференцируемы в точке (х,у), и чтобы в этой точке выполнялись соотношения
 .
.
Доказательство. Необходимость. Здесь мы применим идею, которой воспользовались, когда доказывали, что функция  не имеет производных в точках
не имеет производных в точках  : подойдём к точке z двумя путями - по направлениям
: подойдём к точке z двумя путями - по направлениям  (
( ) и
) и  (
( ).
).
В первом случае: 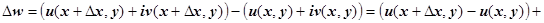
 .
.
Во втором случае: (напомню, что  )
)
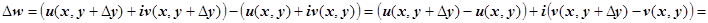
 . Пределы должны быть равны, поэтому
. Пределы должны быть равны, поэтому  .
.
Достаточность. По предположению теоремы, функции  дифференцируемы в точке (х,у), поэтому
дифференцируемы в точке (х,у), поэтому  где
где  ,
,
 - бесконечно малые более высокого порядка по сравнению с
- бесконечно малые более высокого порядка по сравнению с  , т.е.
, т.е.  ,
,  . Найдём
. Найдём  .
. 
 .
.
Последнее слагаемое - бесконечно малая высшего порядка по сравнению с  :
:  ; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим
; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим  на
на  ,
,  на
на  ; тогда
; тогда 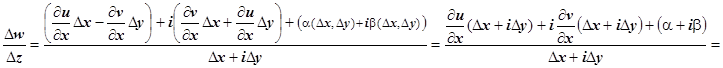
 . Отсюда следует, что существует
. Отсюда следует, что существует  , т.е. функция дифференцируема в точке (х,у).
, т.е. функция дифференцируема в точке (х,у).
Производная дифференцируемой функции может находиться по любой из формул  , эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа:
, эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа:  (в точках, где
(в точках, где  .
.
19.3.3. Примеры вычисления производных.
1. Выше мы доказали, что функция  имеет производную, равную 2z, в каждой точке. Проверим, что для этой функции выполняются условия Коши-Римана. Так как
имеет производную, равную 2z, в каждой точке. Проверим, что для этой функции выполняются условия Коши-Римана. Так как  , то
, то  . Тогда
. Тогда  .
.
2. Для функции  мы получили
мы получили  Поэтому
Поэтому  , т.е. функция дифференцируема.
, т.е. функция дифференцируема.  .
.
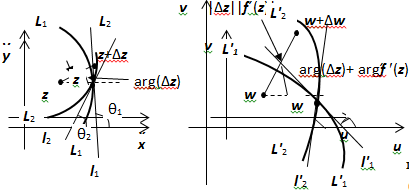
19.3.4. Геометрический смысл производной. Равенство  означает, что
означает, что  , где
, где  . Отсюда, в частности, следует, что если функция дифференцируема в точке, то она непрерывна в этой точке. Будем писать
. Отсюда, в частности, следует, что если функция дифференцируема в точке, то она непрерывна в этой точке. Будем писать  , пренебрегая слагаемым высшего порядка малости. Пусть в точке z существует
, пренебрегая слагаемым высшего порядка малости. Пусть в точке z существует  . Возьмём точки
. Возьмём точки  и
и  ; пусть
; пусть  , тогда
, тогда  . таким образом,
. таким образом,  в
в  больше
больше  ,
,  больше
больше  на
на  для любого
для любого  (с точностью до бесконечно малых высшего порядка). Следовательно, в окрестности любой точки z, в которой
(с точностью до бесконечно малых высшего порядка). Следовательно, в окрестности любой точки z, в которой  , отображение
, отображение  действует следующим образом: любой вектор
действует следующим образом: любой вектор  растягивается в
растягивается в  раз и поворачивается на угол
раз и поворачивается на угол  .
.
19.3.5. Конформность дифференцируемого отображения.
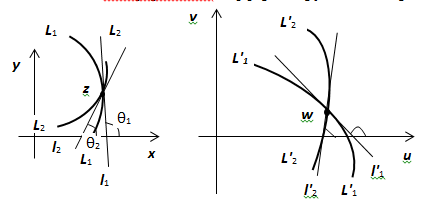
Пусть через точку z проходят две гладкие кривые  и
и  , касательные
, касательные  и
и  к которым образуют с осью Ох углы, соответственно,
к которым образуют с осью Ох углы, соответственно,  и
и  . Образы этих кривых
. Образы этих кривых  и
и  при дифференцируемом отображении
при дифференцируемом отображении  имеют касательные
имеют касательные  и
и  , образующие с действительной осью Ou углы
, образующие с действительной осью Ou углы  и
и  . Согласно предыдущему пункту,
. Согласно предыдущему пункту,  ,
,  , т.е.
, т.е.  . Таким образом, дифференцируемое отображение при
. Таким образом, дифференцируемое отображение при  сохраняет углы между кривыми. Сохраняется и направление отсчёта углов (т.е. если
сохраняет углы между кривыми. Сохраняется и направление отсчёта углов (т.е. если  >
> , то
, то  >
> ).
).
Любое преобразование плоскости в плоскость, обладающее эти свойством (т.е. свойством сохранения углов), называется конформным. Если при этом сохраняется направление отсчёта углов, то преобразование называется конформным преобразованием первого рода; если направление отсчёта углов меняется на противоположное, то преобразование называется конформным преобразованием второго рода. Мы доказали, что аналитическая в некоторой области G функция  осуществляет конформное отображение первого рода во всех точках, в которых производная отлична от нуля.
осуществляет конформное отображение первого рода во всех точках, в которых производная отлична от нуля.
Пример конформного отображения второго рода - недифференцируемая функция  .
.
19.3.6. Гармоничность действительной и мнимой частей дифференцируемой функции. Дифференцируя первое соотношение Коши-Римана  по переменной х, второе соотношение
по переменной х, второе соотношение  по переменной у, получим
по переменной у, получим  , т.е.
, т.е.  (
( - оператор Лапласа), т.е.
- оператор Лапласа), т.е.  - гармоническая функция. Дифференцируя первое соотношение Коши-Римана по переменной у, второе соотношение по переменной х, получим
- гармоническая функция. Дифференцируя первое соотношение Коши-Римана по переменной у, второе соотношение по переменной х, получим  , т.е.
, т.е.  , т.е.
, т.е.  - тоже гармоническая функция. Пара гармонических функций, связанных соотношениями Коши-Римана, называется сопряжёнными функциями.
- тоже гармоническая функция. Пара гармонических функций, связанных соотношениями Коши-Римана, называется сопряжёнными функциями.
Легко доказать, что для любой гармонической в односвязной области D функции  существует единственная (с точностью до постоянного слагаемого) сопряжённая с ней гармоническая функция
существует единственная (с точностью до постоянного слагаемого) сопряжённая с ней гармоническая функция  , т.е. такая функция, что
, т.е. такая функция, что  - аналитическая функция; и наоборот, для любой гармонической
- аналитическая функция; и наоборот, для любой гармонической  существует сопряжённая с ней гармоническая
существует сопряжённая с ней гармоническая  . Пусть, например, дана
. Пусть, например, дана  , обозначим
, обозначим  . Эти функции удовлетворяют условию
. Эти функции удовлетворяют условию  , т.е. векторное поле
, т.е. векторное поле  потенциально. Функцию
потенциально. Функцию  можно найти теперь из системы
можно найти теперь из системы  (как это делается при решении уравнения в полных дифференциалах
(как это делается при решении уравнения в полных дифференциалах  , и как потенциальную для поля
, и как потенциальную для поля  функцию
функцию  .
.
В качестве примера рассмотрим задачу, аналогичную задаче 5 из домашнего задания. Может ли функция  быть мнимой частью некоторой аналитической функции
быть мнимой частью некоторой аналитической функции  ? В случае положительного ответа найти функцию
? В случае положительного ответа найти функцию  .
.
Решение. Докажем, что  - гармоническая функция.
- гармоническая функция.
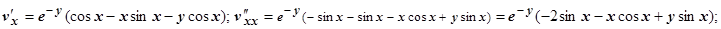

 , т.е.
, т.е.  - гармоническая функция и, следовательно, может являться мнимой частью аналитической функции.
- гармоническая функция и, следовательно, может являться мнимой частью аналитической функции.
Найдём эту функцию. Для действительной части  справедливы соотношения
справедливы соотношения
|
|
|
для нахождения  используем второе уравнение системы:
используем второе уравнение системы: 
 .
.
Ещё посмотрите лекцию "15. Работа с конфиденциальными документами" по этой теме.
Формально мы можем выписать  , но толку в этой записи нет, так как не видна зависимость f от z. Поэтому сделаем по-другому. Выпишем производную
, но толку в этой записи нет, так как не видна зависимость f от z. Поэтому сделаем по-другому. Выпишем производную  :
:  . На действительной оси (при у=0, т.е при
. На действительной оси (при у=0, т.е при ) функция
) функция  превращается в функцию действительной переменной
превращается в функцию действительной переменной  , её производная - в
, её производная - в  . Положим в
. Положим в  у=0, x=z:
у=0, x=z: 
 ; проинтегрировав это выражение, получим
; проинтегрировав это выражение, получим  .
.
Техника нахождения неопределённых интегралов в теории функций комплексной переменной в основном та же, что и в математическом анализе; таблица основных интегралов в обоих случаях одинакова, поскольку одинакова таблица производных. Поэтому


 , где С – произвольная вещественная постоянная интегрирования. Постоянная интегрирования будет действительной, если по условию задачи задана функция
, где С – произвольная вещественная постоянная интегрирования. Постоянная интегрирования будет действительной, если по условию задачи задана функция  , и с точностью до произвольной постоянной находится действительная часть
, и с точностью до произвольной постоянной находится действительная часть  функции
функции  ; если же задана функция
; если же задана функция  , то и с точностью до произвольной постоянной интегрирования находится мнимая часть
, то и с точностью до произвольной постоянной интегрирования находится мнимая часть  , т.е постоянная будет чисто мнимым числом
, т.е постоянная будет чисто мнимым числом  (произвольное вещественное число).
(произвольное вещественное число).
Проверим полученный результат. Если  , то
, то 

 ;
;
 ; условия Коши-Римана выполнены, следовательно, функция
; условия Коши-Римана выполнены, следовательно, функция  - аналитическая на всей комплексной плоскости функция.
- аналитическая на всей комплексной плоскости функция.
Во всех этих рассуждениях мы проигнорировали вопрос о том, имеют ли функции u и v производные порядка выше первого? (Существование первых производных следует, как мы видели, из дифференцируемости f(z)). Дальше мы докажем, что, в отличие от действительного случая, ФКП обладает удивительным свойством - если она аналитична в некоторой области (т.е. в каждой точке этой области имеет первую производную), то она бесконечно дифференцируема в этой области (т.е. в каждой точке этой области она имеет производную любого порядка). Как следствие, функции u и v тоже бесконечно дифференцируемы.



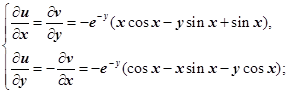
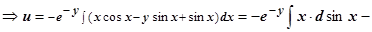
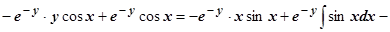
 ,
,

















