Дифференцируемость функции комплексной переменной
Дифференцируемость функции комплексной переменной.
19.3.1. Определение производной. Аналитичность ФКП. Пусть  определена, однозначна и принимает собственные значения в окрестности точки
определена, однозначна и принимает собственные значения в окрестности точки  . Производной функции
. Производной функции  в точке
в точке  называется предел
называется предел  . Функция, имеющая конечную производную в точке
. Функция, имеющая конечную производную в точке  , называется дифференцируемой в этой точке.
, называется дифференцируемой в этой точке.
В этом определении важно, что стремление  может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной
может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной  не сводится к существованию частных производных функций
не сводится к существованию частных производных функций  и
и  , а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функции в точке и в области.
, а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функции в точке и в области.
Определение. Однозначная функция называется аналитической (регулярной, голоморфной) в точке  , если она дифференцируема в некоторой окрестности этой точки.
, если она дифференцируема в некоторой окрестности этой точки.
Однозначная функция называется аналитической в области D, если она аналитична в каждой точке этой области.
Примеры. 1.  . В этом случае
. В этом случае 
 . Таким образом , эта функция дифференцируема в любой точке, и её производная равна 2z.
. Таким образом , эта функция дифференцируема в любой точке, и её производная равна 2z.
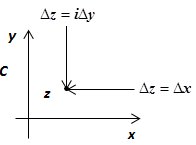
2.  Докажем, что эта функция не имеет производной ни в какой точке
Докажем, что эта функция не имеет производной ни в какой точке  . Будем стремить
. Будем стремить  по двум путям: по прямой, параллельной действительной оси Ох (в этом случае
по двум путям: по прямой, параллельной действительной оси Ох (в этом случае  ), и по прямой, параллельной мнимой оси Оу (в этом случае
), и по прямой, параллельной мнимой оси Оу (в этом случае  ). В первом случае
). В первом случае  , во втором
, во втором 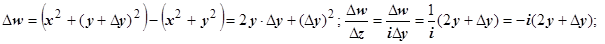
 . Эти пределы равны, только если
. Эти пределы равны, только если 
 . Таким образом, функция
. Таким образом, функция  может быть дифференцируема в единственной точке
может быть дифференцируема в единственной точке  , во всех остальных точках пределы
, во всех остальных точках пределы  различны в зависимости от способа стремления
различны в зависимости от способа стремления  , т.е.
, т.е.  не существует.
не существует.
19.3.2. Условия Коши-Римана (Даламбера-Эйлера).Сейчас мы сформулируем и докажем важнейшую в теории ФКП теорему о необходимых и достаточных условиях дифференцируемости (а, следовательно, аналитичности) функции.
Рекомендуемые материалы
Для того, чтобы функция  была дифференцируема в точке
была дифференцируема в точке  , необходимо и достаточно, чтобы функции
, необходимо и достаточно, чтобы функции  и
и  были дифференцируемы в точке (х,у), и чтобы в этой точке выполнялись соотношения
были дифференцируемы в точке (х,у), и чтобы в этой точке выполнялись соотношения
 .
.
Доказательство. Необходимость. Здесь мы применим идею, которой воспользовались, когда доказывали, что функция  не имеет производных в точках
не имеет производных в точках  : подойдём к точке z двумя путями - по направлениям
: подойдём к точке z двумя путями - по направлениям  (
( ) и
) и  (
( ).
).
В первом случае: 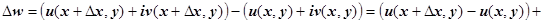
 .
.
Во втором случае: (напомню, что  )
)
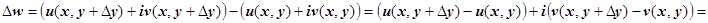
 . Пределы должны быть равны, поэтому
. Пределы должны быть равны, поэтому  .
.
Достаточность. По предположению теоремы, функции  дифференцируемы в точке (х,у), поэтому
дифференцируемы в точке (х,у), поэтому  где
где  ,
,
Бесплатная лекция: "Часть 1" также доступна.
 - бесконечно малые более высокого порядка по сравнению с
- бесконечно малые более высокого порядка по сравнению с  , т.е.
, т.е.  ,
,  . Найдём
. Найдём  .
. 
 .
.
Последнее слагаемое - бесконечно малая высшего порядка по сравнению с  :
:  ; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим
; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим  на
на  ,
,  на
на  ; тогда
; тогда 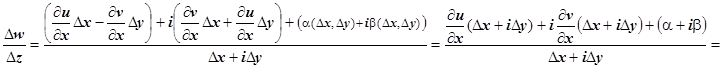
 . Отсюда следует, что существует
. Отсюда следует, что существует  , т.е. функция дифференцируема в точке (х,у).
, т.е. функция дифференцируема в точке (х,у).
Производная дифференцируемой функции может находиться по любой из формул  , эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа:
, эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа:  (в точках, где
(в точках, где  .
.
19.3.3. Примеры вычисления производных.
1. Выше мы доказали, что функция  имеет производную, равную 2z, в каждой точке. Проверим, что для этой функции выполняются условия Коши-Римана. Так как
имеет производную, равную 2z, в каждой точке. Проверим, что для этой функции выполняются условия Коши-Римана. Так как  , то
, то  . Тогда
. Тогда  .
.
2. Для функции  мы получили
мы получили  Поэтому
Поэтому  , т.е. функция дифференцируема.
, т.е. функция дифференцируема.  .
.




















