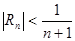Признак Лейбница
Признак Лейбница.
Пусть
1. ряд  имеет вид
имеет вид  (знакочередующийся,
(знакочередующийся,  )
)
2. последовательность  монотонно убывает
монотонно убывает
3. 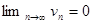
Тогда 1) ряд  сходится
сходится
2) 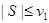
Доказательство. Рассмотрим последовательность частичных сумм с четными номерами
Рекомендуемые материалы
 (последовательность
(последовательность  монотонно убывает по условию теоремы).
монотонно убывает по условию теоремы).
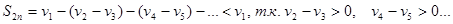
Т.е. последовательность  ограничена сверху
ограничена сверху  .
.
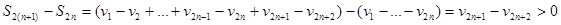
Т.е. последовательность  монотонно возрастает.
монотонно возрастает.
По теореме Вейерштрасса существует  .
.
Рассмотрим теперь последовательность частичных сумм с нечетными номерами
 .
.
По условию 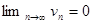 , т.е.
, т.е.  .
.
По доказанному выше  . Следовательно, предел правой части равенства существует и равен
. Следовательно, предел правой части равенства существует и равен  . Поэтому предел левой части равенства тоже существует и равен
. Поэтому предел левой части равенства тоже существует и равен
 .
.
Раскроем определение предела  как для четных n, так и для нечетных n. Следовательно, это справедливо для любых
как для четных n, так и для нечетных n. Следовательно, это справедливо для любых  , поэтому
, поэтому  .
.
Из доказанного выше неравенства  . Переходя к пределу, получим
. Переходя к пределу, получим  .
.
Обратите внимание на лекцию "8 Художественная культура Древней Греции".
Следствие.  . Остаток ряда оценивается модулем первого отброшенного члена ряда.
. Остаток ряда оценивается модулем первого отброшенного члена ряда.
Доказательство. Так как остаток знакочередующегося ряда тоже знакочередующийся ряд, то его сумма по признаку Лейбница оценивается модулем его первого члена.
То есть  . А первый член остатка ряда и есть первый отброшенный член.
. А первый член остатка ряда и есть первый отброшенный член.
Пример. Ряд 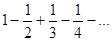
 . Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.
. Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.