Линейное программирование
ЛЕКЦИЯ 2
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Постановка задачи линейного программирования. Математическая модель задачи. Примеры задач линейного программирования. Графический метод решения задачи. Симплекс– метод решения задачи линейного программирования. Анализ решения задачи линейного программирования.
Линейное программирование (ЛП) является одной из основных частей того раздела современной математики, который получил название математического программирования. В задачах ЛП используется линейная модель, в которой функция цели f(х) линейна, ограничения являются либо линейными равенствами, либо линейными неравенствами.
Линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания (имеются ввиду действия между переменными, умножение, скажем, переменной на константу не делает зависимость нелинейной).
Если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости являются нелинейными. При этом следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то и вся задача является нелинейной.
В общей постановке задача формулируется как нахождение оптимального (наибольшего, наименьшего, или такого, что равно какому-то значению) значения целевой функции для определенной области изменения ее аргументов, определяемой системой ограничений. Для решения задачи формируется ее математическая модель.
Общая форма модели задачи ЛП характеризуется следующим образом:
Рекомендуемые материалы
Найти совокупность значений n переменных х1, х2,…,хn, удовлетворяющих системе ограничений:
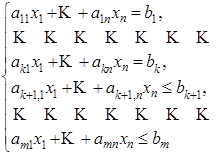
и условиям неотрицательности:
 ,
,
для которых линейная функция (целевая функция)

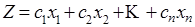
достигает экстремума (максимума или минимума).
Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач.
Задачи распределения ресурсов. Такие задачи возникают при определении оптимального плана производства продукции, учитывающего имеющиеся в наличии материальные, людские, финансовые и другие виды ресурсы. Считаются известными виды продукции, виды используемых ресурсов, запасы ресурсов, расход ресурсов каждого вида на производство единицы каждого вида продукции, цена, по которой может быть продана единица продукции каждого вида. План считается оптимальным по какому-то выбранному критерию, например, максимуму прибыли, минимуму расходов, максимуму объемов готовой продукции, минимуму использования ресурсов и т.д.
Пример.
Задачи о смесях. Такие задачи возникают при выборе способа смешения заданных ингредиентов для получения смеси с определенными свойствами. Смесь должна содержать определенное количество компонентов, входящих в состав исходных ингредиентов. Стоимость ингредиентов известна. Обычно требуется получить смесь с наименьшими затратами.
За неизвестные переменные в модели оптимального смешивания принимаются количества или доли ингредиентов, необходимых для приготовления смеси.
Пример.
Задачи о раскрое материалов. Задача оптимального раскроя материалов заключается в определении наиболее рационального способа раскроя имеющегося материала (бревна, стальные полосы, кожа и т.д.), при котором будет изготовлено наибольшее количество готовых изделий в заданном ассортименте или будет достигнуто наименьшее количество отходов.
Пусть на обработку поступает a единиц сырьевого материала одного вида (например, a бревен одной длины). Из него требуется изготовить комплекты, в каждый из которых входит n видов изделий в количестве, пропорциональном числам  . Имеется m способов раскроя (обработки) данного материала, т.е. известны величины
. Имеется m способов раскроя (обработки) данного материала, т.е. известны величины  определяющие количество единиц j-х изделий при i-м способе раскроя единицы сырьевого материала. Требуется определить план раскроя, обеспечивающий максимальное количество комплектов.
определяющие количество единиц j-х изделий при i-м способе раскроя единицы сырьевого материала. Требуется определить план раскроя, обеспечивающий максимальное количество комплектов.
Пример.
Графический метод решения задачи ЛП
Графический метод применяется для решения задач линейного программирования с двумя переменными и основан на геометрической интерпретации, согласно с которой графически можно изобразить множество точек, координаты которых удовлетворяют все ограничения задачи — многоугольник решений и следующих аналитических свойствах задач линейного программирования: если задача линейного программирования имеет оптимальный план, то экстремальное значение целевая функция приобретает в одной из вершин ее многоугольника решений. Если же целевая функция достигает экстремального значения более чем в одной вершине многоугольника, то она достигает его и в любой точке, которая является линейной комбинацией этих вершин.
Следовательно, решить задачу линейного программирования графически означает найти такую вершину многоугольника решений, в результате подстановки координат которой в функцию цели она получает наибольшее (наименьшего) значение.
Алгоритм графического метода решения задачи состоит из таких шагов:
1. строим на координатной плоскости множество допустимых решений задачи;
2. строим произвольную линию уровня целевой функции так, чтобы она пересекала допустимое множество и так, чтобы точки допустимого множества лежали по обе стороны от линии уровня;
3. строим вектор N(с1, с2) и, передвигая линию уровня Z = с1x1 + с2x2 в направлении вектора (если решается задача минимизации, то линию уровня передвигаем в направлении, противоположному N) параллельно к самой себе, приходим к такому положению, когда линия уровня и множество допустимых решений задачи будут иметь лишь одну общую точку;
4. вычисляем координаты точек, в которых опорная линия уровня целевой функции пересекает множество допустимых решений задачи, решая соответствующие системы двух линейных равнений с двумя неизвестными;
5. вычисляем оптимальное значение целевой функции Z, подставляя вместо ее аргументов координаты произвольного оптимального решения.
Замечание. Если окажется, что линия уровня параллельная одной из сторон многоугольного решений, то в этом случае оптимум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесконечное множество решений. Говорят, что такая задача имеет альтернативный оптимум.
Один из вариантов задачи ЛП может быть записан в виде:
| Найти при условиях | max Z(X) = c1 x1 + c2 x2, a11 x1 + a12 x2 £ b1 , a21 x1 + a22 x2 ³ b2 , a31 x1 + a32 x2 £ b3 , x1 ³ 0, x2 ³ 0. | (1) |
В целом ограничения (1) вырезают на плоскости некоторый выпуклый многоугольник, расположенный в первом квадранте.
В теории линейного программирования строго доказано, что линейная форма в n-мерном пространстве принимает экстремальные значения в вершинах многогранника условий. В принципе, решение может быть найдено перебором вершин такого многогранника. Разработан специальный симплекс-метод, который позволяет сделать такой перебор направленным и получить искомое решение за значительно меньшее количество шагов.
Используя геометрическую интерпретацию, легко показать два основных случая, когда решение задачи ЛП отсутствует.
В первом случае решение отсутствует из-за несовместности (противоречивости) ограничений задачи ЛП. Примером этого может служить система ограничений, показанная на рис. 1. Полуплоскости, допустимые по отношению к соответствующему ограничению, на рис. 1 указаны стрелками. Из рисунка видно, что ни одна точка плоскости не удовлетворяет одновременно трем приведенным ограничениям, что означает отсутствие допустимых решений, а значит, и оптимального плана (решения) задачи ЛП для любой линейной целевой функции.
Во втором случае решение задачи ЛП отсутствует из-за неограниченности значения целевой функции. Примером этого может служить, геометрическая интерпретация условий задачи представленная на рис. 2, где показано произвольное положение прямой Z(х). Область допустимых планов задачи ЛП не пуста, но не замкнута. Из рисунка видно, что при перемещении прямой Z(х) параллельно самой себе вправо вверх значение максимизируемой функции неограниченно возрастает, что и означает отсутствие решения заданной задачи ЛП.
Заметим, что в случае минимизации заданной линейной формы при тех же ограничениях задача ЛП имеет оптимальное решение в точке А.
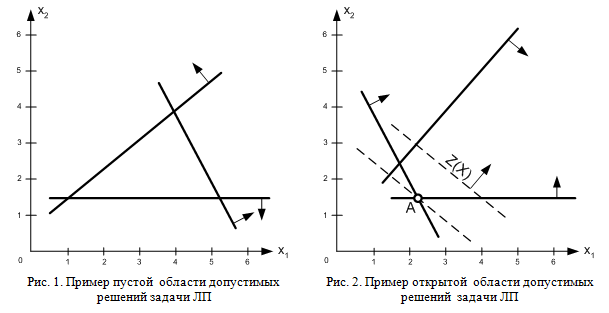
Область допустимых решений – это область, полученная путем графического отображения ограничений конкретной задачи и включающая все возможные решения оптимизации.
Для иллюстрации графического способа рассмотрим два примера, в первом находится максимум функции цели, во втором – минимум.
Симплекс – метод решения задачи ЛП
Симплекс-метод – итеративный процесс, предназначенного для определения оптимального решения за конечное число шагов. Первый шаг состоит в построении начального допустимого решения; затем определяется, является ли оно оптимальным, т. е. достигнут ли максимум или минимум целевой функции. Если это условие выполнено, то задача решена. В противном случае строится новое решение и основные шаги повторяются. Симплекс-метод имеет определенные правила, облегчающие выбор вводимой и удаляемой переменных и, соответственно, процесс решения.
В обычном симплекс-методе принимается предпосылка о максимизации целевой функции задачи линейного программирования в условиях системы ограничений со знаком "<". Это означает, что при реализации симплекс-алгоритма в качестве начальной крайней точки может быть выбрано начало координат. Поиск оптимального решения всегда начинается со значения целевой функции, равного нулю.
Симплекс-алгоритм состоит из следующих шагов.
Шаг 0. Используя линейную модель стандартной формы, определяют начальное допустимое базисное решение путем приравнивания к нулю п–т небазисных переменных.
Шаг 1. Из числа текущих небазисных (равных нулю) переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, так как текущее базисное решение оптимально. В противном случае осуществляется переход к шагу 2.
Шаг 2. Из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение (стать небазисной) при введении в состав базисных новой переменной.
Шаг 3. Находится новое базисное решение, соответствующее новым составам небазисных и базисных переменных. Переход к шагу 1.
Поясним процедуры симплекс-метода на следующем примере. Требуется найти максимум целевой функции для задачи, математическая модель которой имеет следующий вид:
целевая функция
z - 3x1 - 2x2 = 0
ограничения
x1 + 2x2 + x3 = 6
2x1 + x2+x4 = 8
x2 – x1 + x5 = 1
x2 +x6 = 2
В качестве начального пробного решения используется решение системы уравнений, в которой две (в задаче 6 переменных и 4 ограничения, поэтому 6-4=2) переменные принимаются равными нулю. Это обеспечивает единственность и допустимость получаемого решения. В рассматриваемом случае очевидно, что подстановка x1 = x2 = 0 сразу же приводит к следующему результату: x3 = 6, x4 =8, x5 =1 и x6 = 2. эти значения переменных можно использовать как начальное допустимое решение. Величина z в этом случае равна нулю, так как и x1, и x2 имеют нулевое значение (это имеет место во всех случаях, когда начальный базис состоит из остаточных переменных).
Полученные результаты оформим в виде так называемой симплекс–таблицы, которую сформируем следующим образом. Представим коэффициенты, стоящие в левой части системы ограничений, в матричной форме. За обозначения столбцов примем переменные, которым они соответствуют. Значения правой части ограничений запишем в отдельном столбце матрицы справа. За обозначения строк примем обозначения соответствующих переменных, которые являются базисными (имеющими ненулевые значения) переменными. Наконец, введем в таблицу дополнительную строку, соответствующую коэффициентам целевой функции Z, которые, требуется вводить с отрицательным знаком.
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
| X3 | 1 | 2 | 1 | 0 | 0 | 0 | 6 |
| X4 | 2 | 1 | 0 | 1 | 0 | 0 | 8 |
| X5 | -1 | 1 | 0 | 0 | 1 | 0 | 1 |
| X6 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
| Z | -3 | -2 | 0 | 0 | 0 | 0 | 0 |
В сформированной симплекс–таблице столбец Базисные переменные содержит переменные пробного базиса : x3, x4, x5 и x6, значения которых приведены в столбце Решение. При этом подразумевается, что небазисные переменные x1 и x2 (не представленные в первом столбце) равны нулю. Значение целевой функции равно нулю, что и показано в последнем столбце таблицы.
Условие оптимальности. Если в задаче максимизации все небазисные переменные в строке Z имеют неотрицательные коэффициенты, полученное пробное решение является оптимальным. В противном случае в качестве новой базисной переменной следует выбрать ту, которая имеет наибольший по абсолютной величине отрицательный коэффициент.
Нетрудно заметить, что обе небазисные переменные х1 и x2, равные нулю, имеют в строке Z отрицательные коэффициенты. Следовательно, решение не является оптимальным. Для улучшения полученного решения в соответствии с условием оптимальности выбираем переменную x1 с большим абсолютным значением отрицательного коэффициента в строке Z, так как практический опыт вычислений показывает, что в этом случае оптимум достигается быстрее. Столбец, соответствующий выбранной переменной x1 называется ведущим.
Разделим значения в столбце Решение на соответствующие значения ведущего столбца. Строки, в которых элементы ведущего столбца имеют отрицательные и нулевые элементы во внимание не принимаются. В результате получим ряд отношений.
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
|
| X3 | 1 | 2 | 1 | 0 | 0 | 0 | 6 | 6/1=6 |
| X4 | 2 | 1 | 0 | 1 | 0 | 0 | 8 | 8/2=4 |
| X5 | -1 | 1 | 0 | 0 | 1 | 0 | 1 | |
| X6 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | |
| Z | -3 | -2 | 0 | 0 | 0 | 0 | 0 |
Условие допустимости. В качестве исключаемой переменной выбирается та из переменных текущего базиса, которая первой обращается в нуль при увеличении включаемой переменной
В соответствии с этим условием выберем среди полученных отношений наименьшее. В нашем случае оно равно 4. Соответствующая ему строка X4 называется ведущей. Переменная X4 исключается из базиса.
Процедура выбора исключаемой переменной предполагает проверку условия допустимости, требующего, чтобы в качестве исключаемой переменной выбиралась та из переменных текущего базиса, которая первой обращается в нуль при увеличении включаемой переменной x1.
Элемент таблицы, находящийся на пересечении ведущего столбца и ведущей строки, будем называть ведущим элементом.
После того как определены включаемая и исключаемая переменные (с использованием условий оптимальности и допустимости), следующая итерация (поиск нового базисного решения) осуществляется методом исключения переменных, или методом Жордана – Гаусса.
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
|
| X3 | 0 | 3/2 | 1 | -1/2 | 0 | 0 | 2 | 4/3 |
| X1 | 1 | 1/2 | 0 | 1/2 | 0 | 0 | 4 | 2 |
| X5 | 0 | 3/2 | 0 | 1/2 | 1 | 0 | 5 | 10/3 |
| X6 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | 2 |
| Z | 0 | -1/2 | 0 | 3/2 | 0 | 0 | 12 |
Оптимальное решение.
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
|
| X2 | 0 | 1 | 2/3 | -1/3 | 0 | 0 | 11/3 | |
| X1 | 1 | 0 | -1/3 | 2/3 | 0 | 0 | 31/3 | |
| X5 | 0 | 0 | -1 | 1 | 1 | 0 | 3 | |
| X6 | 0 | 0 | -2/3 | 1/3 | 0 | 1 | 2/3 | |
| Z | 0 | 0 | 1/3 | 4/3 | 0 | 0 | 121/3 |
Статус ресурсов
Статус ресурсов (дефицитный или недефицитный) для любой модели ЛП можно установить непосредственно из результирующей симплекс-таблицы, обращая внимание на значения остаточных переменных. Применительно к рассмотренной задаче можно привести следующую сводку результатов:
| Ресурс | Остаточная переменная | Статус ресурса |
| Исходный продукт А | S10= | Дефицитный |
| Исходный продукт B | S2=0 | Дефицитный |
| Превышение объема краски В по отношению к объему производства краски Н | S3=3 | Недефицитный |
| Спрос на краску В | S4=2/3 | Недефицитный |
Положительное значение остаточной переменной указывает на неполное использование соответствующего ресурса, т. е. данный ресурс является недефицитным. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении соответствующего ресурса. Из таблицы видно, что ресурсы 3 и 4, связанные с возможностями сбыта продукции, являются недефицитными. Поэтому любое увеличение их запасов сверх установленного максимального значения приведет лишь к тому, что они станут еще более недефицитными. Оптимальное решение задачи при этом останется неизменным.
Ресурсы, увеличение запасов которых позволяет улучшить решение (увеличить прибыль),– это исходные продукты А и В, поскольку из симплекс-таблицы для оптимального решения видно, что они дефицитные. В связи с этим логично поставить следующий вопрос: какому из дефицитных ресурсов следует отдать предпочтение при вложении дополнительных средств на увеличение их запасов, с тем чтобы получить от них максимальную отдачу?
Ценность ресурса
Ценность ресурса характеризуется величиной улучшения оптимального значения г, приходящегося на единицу прироста объема данного ресурса.
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
| Z | 0 | 0 | 1/3 | 4/3 | 0 | 0 | 121/3 |
Ценность ресурсов всегда можно определить по значениям коэффициентов при переменных начального базиса, фигурирующих в z-уравнении оптимальной симплекс-таблицы. Так как переменная s; всегда связана только с ресурсом i, идентификация ресурса по коэффициентам не вызывает затруднений.
Максимальное изменение запаса ресурса.
При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используются теневые цены. Требуемая информация может быть получена из симплекс–таблицы для оптимального решения.
Положим, что в нашем примере запас первого ресурса изменился D1, т.е. запас продукта А составит 6+D1 тонн. При положительной величине D1 запас данного ресурса увеличивается, при отрицательной – уменьшается.
Так как введение D1 сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Поэтому D1 не может принимать значений, при которых какая-либо из (базисных) переменных становится отрицательной. Из этого следует, что величина D1 должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений в результирующей симплекс-таблице, т.е.
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
| X2 | 0 | 1 | 2/3 | -1/3 | 11/3 | ||
| X1 | 1 | 0 | -1/3 | 2/3 | 31/3 | ||
| X5 | 0 | 0 | -1 | 1 | 1 | 3 | |
| X6 | 0 | 0 | -2/3 | 1/3 | 1 | 2/3 | |
| Z | 0 | 0 | 1/3 | 4/3 | 0 | 0 | 121/3 |
x1 = 11/3 + (2/3)D1 ³ 0 (1)
x2 = 31/3 – (1/3)D1 ³ 0 (2)
s3 = -3 – D1 ³ 0 (3)
s4 = 2/3 – (2/3)D1 ³ 0 (4)
Для определения допустимого интервала изменения D1 рассмотрим два случая.
Случай 1: D1 > 0. Соотношение (1) всегда выполняется при D1 > 0. Соотношения (2), (3) и (4) определяют следующие предельные значения D1: D1 £ 10, D1 £ 3и D1 £ l. Таким образом, все четыре соотношения выполняются при D1 £ l.
Случай 2: D1 < 0. Соотношения (2), (3) и (4) всегда выполняются при D1 < 0, тогда как соотношение (1) справедливо только при D1 ³ –2.
Объединяя результаты, полученные для обоих случаев, можно сделать вывод, что при –2 £ D1 £ l решение рассматриваемой задачи всегда будет допустимым. Любое значение D1 , выходящее за пределы указанного интервала (т. е. уменьшение запаса продукта А более чем на 2 т или увеличение более чем на 1 т), приведет к недопустимости решения и новой совокупности базисных переменных
Максимальное изменение коэффициентов
удельной прибыли (стоимости)
Любые изменения коэффициентов целевой функции оказывают влияние только на z-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Задача заключается в том, чтобы найти интервалы значений изменений коэффициентов целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными.
Положим, что в нашем примере удельная прибыль от производства краски для наружных работ (переменная xE) изменяется от 3 до 3+d1, где d1 может быть как положительным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:
z = (3 + d1)xE + 2xI
Если воспользоваться данными начальной симплекс-таблицы и выполнить все вычисления, необходимые для получения заключительной симплекс-таблицы, то последнее z-уравнение будет иметь вид:
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
| Z | 0 | 0 | 1/3-1/3d1 | 4/3+2/3d1 | 0 | 0 | 121/3+10/3d1 |
Коэффициенты при базисных переменных x1, x2 и остаточных переменных s3, s4 остаются равными нулю. Это уравнение отличается от z-уравнения до введения d1 только наличием членов, содержащих d1. Коэффициенты при d1 равны коэффициентам при соответствующих переменных в xE-уравнении симплекс-таблицы для полученного ранее оптимального решения
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Решение |
| X1 | 1 | 0 | -1/3 | 2/3 | 31/3 |
Мы рассматриваем .x1-уравнение, так как коэффициент именно при этой переменной в выражении для целевой функции изменился на d1 .
15. Предромантизм - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
Оптимальные значения переменных будут оставаться неизменными при значениях d1 удовлетворяющих условию неотрицательности (задача на отыскание максимума) всех коэффициентов при небазисных переменных в z-уравнении. Таким образом, должны выполняться следующие неравенства:
1/3 – d1/3 ³ 0
4/3 – 2d1/3 ³ 0
Из первого неравенства получаем, что d1 £ l, а из второго — d1 ³ –2. Эти результаты определяют пределы изменения коэффициента ci:
-2 £ d1 £.1
Таким образом, при уменьшении коэффициента целевой функции при переменной xE до значения, равного 3+ (–2) = 1, или при его увеличении до 3+1 = 4 оптимальные значения переменных остаются неизменными. Однако оптимальное значение z будет изменяться (в соответствии с выражением 121/3+10/3d1 , где -2 £ d1 £.1).


















