Теория игр и принятия решений
Глава III
Теория игр и принятия решений
3.1. Условия принятия решений
В теории принятия решений используются "разумные" процедуры выбора наилучшей из нескольких возможных альтернатив. Доброкачественность выбранного решения зависит от качества данных, используемых при описании ситуации, в которой принимается решение. С этой точки зрения процесс принятия решений может принадлежать к одному из трех возможных условий.
1. Принятие решений в условиях определенности, когда данные известны точно.
2. Принятие решений в условиях риска, когда данные можно описать с помощью вероятностных распределений.
3. Принятие решений в условиях неопределенности, когда данным нельзя приписать относительные веса (весовые коэффициенты), которые представляли бы степень их значимости в процессе принятия решений.
По существу, в условиях определенности данные надежно определены, в условиях неопределенности они не определены.* Принятие решений в условиях риска, следовательно, представляет "промежуточный" случай.
В этой главе представлены некоторые модели принятия решений, относящиеся к указанным трем условиям.
Рекомендуемые материалы
3.2. Принятие решений в условиях определенности
Модели линейного программирования являются примером принятия решений в условиях определенности. Эти модели применимы лишь в тех случаях, когда альтернативные решения можно связать между собой точными линейными функциями. В этом разделе рассматривается иной подход к принятию решений в ситуациях, когда, например, для идей, чувств, эмоций определяются некоторые количественные показатели, обеспечивающие числовую шкалу предпочтений для возможных альтернативных решений. Этот подход известен как метод анализа иерархий.
3.2.1. Метод анализа иерархий
Перед тем как изложить детали данного метода, рассмотрим пример, демонстрирующий способ, с помощью которого оцениваются различные альтернативные решения.
Пример 3.2-1
Мартин Ганс – выпускник-отличник средней школы, который получил полную стипендию от трех университетов: А, В и С. В целях выбора университета Мартин сформулировал два основных критерия: местонахождение университета и его академическая репутация. Будучи отличным учеником, он оценивает академическую репутацию университета в пять раз выше, чем его местонахождение. Это приводит к тому, что репутации университета приписывается вес примерно 83 %, а его местонахождению – 17 %. Далее Мартин использует системный анализ, (сущность его излагается ниже), для оценки трех университетов с точки зрения их местонахождения и репутации. Проведенный анализ дает следующие оценки.
|
| Университет | ||
| A | B | C | |
| Местонахождение | 12.9% | 27.7% | 59.4% |
| Репутация | 54.5% | 27.3% | 18.2% |
Структура задачи принятия решений приведена на рис. 14.1. Задача имеет единственный иерархический уровень с двумя критериями (местонахождение и репутация) и три альтернативных решения (университеты А, В и С).
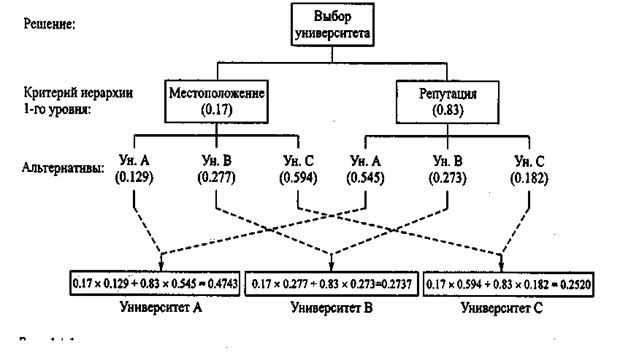
Рис. 14.1
Оценка трех университетов основана на вычислении комбинированного весового коэффициента для каждого из них.
Университет А: 0.17 х 0.129 + 0.83 х 0.545 = 0.4743.
Университет В: 0.17 х 0.277 + 0.83 х 0.273 = 0.2737.
Университет С: 0.17 x 0.594 + 0.83 x 0.182 = 0.2520.
На основе этих вычислений университет А получает наивысший комбинируя ванный вес и, следовательно, является наиболее оптимальным выбором Мартина.
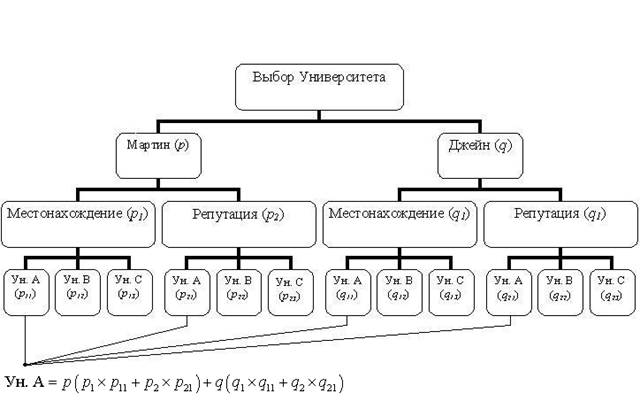
Общая структура метода анализа иерархий может включать несколько иерархическая уровней со своими критериями. Предположим в примере 3.2-1, что сестра-близнец Мартина Джейн также получила полную стипендию от трех университетов. Однако их родители ставят условие, что дети должны учиться в одном университете, тогда они смогут пользоваться одним автомобилем. На рис. 14.2 приведена структура задачи выбора решения, которая теперь включает два иерархических уровня со своими критериями. Величины р и q (предположительно равные) на первом иерархическом уровне представляй ют собой весовые коэффициенты, которые приписываются точке зрения Мартина и Джейн относительно процесса выбора, соответственно. Второй иерархический уровень использует веса (р1, р2) и (q1, q2) для отображения индивидуальных точек зрения Мартина и Джейн относительно критериев местонахождения и академической репутации каждого университета. Остальная часть структуры принятия решения может быть интерпретирована аналогично предыдущему примеру. Заметим, что 
 . Определение комбинированного веса для университета А, представленное на рис. 14.2, демонстрирует, каким образом вычисляются эти показатели.
. Определение комбинированного веса для университета А, представленное на рис. 14.2, демонстрирует, каким образом вычисляются эти показатели.
3.2.2. Упражнение 3.2, а
1. Пусть для задачи выбора университета Мартином и Джейн установлены следующие значения весовых коэффициентов.
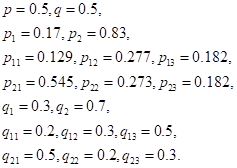
основываясь на этой информации, оцените с помощью комбинированных весов каждый из трех университетов.
Определение весовых коэффициентов. Сложность метода анализа иерархий заключается в определении относительных весовых коэффициентов (таких, какие использованы в примере 3.2. – 1) для оценки альтернативных решений. Если имеется n критериев на заданном уровне иерархии, соответствующая процедура задает матрицу А размерности  , именуемую матрицей парных сравнений, которая отражает суждение лица, принимающего решения, относительно важности различных критериев. Парное сравнение выполняется таким образом, что критерий в строке i (i = 1, 2, …, n) оценивается относительно каждого из критериев, представленных n столбцами. Обозначим через aij = 1 элемент матрицы А, находящийся на пересечении i-й строки и j-го столбца. В соответствии с методом анализа иерархий для описания упомянутых оценок используются целые числа от 1 до 9. При этом aij = 1 означает, что i-й и j-й критерии одинаково важны, aij = 5 отражает мнение, что i-й критерий значительно важнее j-го, а aij = 9 указывает, что i-й критерий чрезвычайно важнее j-го. Другие промежуточные значения между 1 и 9 интерпретируются аналогично. Согласованность таких обозначений обеспечивается следующим условием: если aij = k, то автоматически = 1/k. Кроме того, все диагональные элементы aii матрицы А должны быть равны 1, так как они выражают оценку критерия относительно самих себя.
, именуемую матрицей парных сравнений, которая отражает суждение лица, принимающего решения, относительно важности различных критериев. Парное сравнение выполняется таким образом, что критерий в строке i (i = 1, 2, …, n) оценивается относительно каждого из критериев, представленных n столбцами. Обозначим через aij = 1 элемент матрицы А, находящийся на пересечении i-й строки и j-го столбца. В соответствии с методом анализа иерархий для описания упомянутых оценок используются целые числа от 1 до 9. При этом aij = 1 означает, что i-й и j-й критерии одинаково важны, aij = 5 отражает мнение, что i-й критерий значительно важнее j-го, а aij = 9 указывает, что i-й критерий чрезвычайно важнее j-го. Другие промежуточные значения между 1 и 9 интерпретируются аналогично. Согласованность таких обозначений обеспечивается следующим условием: если aij = k, то автоматически = 1/k. Кроме того, все диагональные элементы aii матрицы А должны быть равны 1, так как они выражают оценку критерия относительно самих себя.
Пример 3.2-2
Покажем как определяется матрица сравнения А для задачи выбора Мартина из примера 3.2.–1. Начнем с главного иерархического уровня, который имеет дело с критериями академической репутации и его местонахождения. С точки зрения Мартина академическая репутация университета значительно важнее его местонахождения. Следовательно, он приписывает элементу (1,2) матрицы А значение 5, т.е. a12=5. это автоматически предполагает, что a21=1/5/ обозначив через R и L критерии репутации университета и его местонахождения, можно записать матрицу сравнения следующим образом.
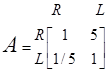
относительно веса критериев R и L могут быть определены путем деления элементов каждого столбца на сумму элементов этого же столбца. Следовательно, для нормализации матрицы А делим элементы первого столбца на величину 1 + 1/5 — 1.2, элементы второго – на величину 5 + 1=6. Искомые относительные веса wR и wL критериев вычисляются теперь в виде средних значений элементов соответствующих строк нормализованной матрицы А. Следовательно,
|
| средние значения элементов строк
|
В результате вычислений получили wR = 0.83 и wL = 0.17, т.е. те веса, которые показаны на рис. 14.1. Столбцы матрицы N одинаковы, что имеет место лишь в случае, когда лицо, принимающее решение, проявляет идеальную согласованность в определении элементов матрицы А. Этот тезис детальнее обсуждается ниже.
Относительные веса альтернативных решений, соответствующих университетам А, В и С, вычисляются в пределах каждого критерия R и L с использованием следующих двух матриц сравнения.
 ,
,
Сумма элементов столбцов = [1.83, 3.67, 5.5],
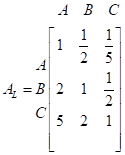
Сумма элементов столбцов = [8, 3.5, 1.7].
Элементы матриц AR и AL, определены на основе суждений Мартина, касающихся относительной важности трех университетов.
При делении элементов каждого столбца матриц AR и AL на сумму элементов этих же столбцов получаем следующие нормализованные матрицы.
|
| средние значения элементов строк
|
|
| средние значения элементов строк
|
Величины (wra, wrb, wrc) = (0.545, 0.273, 0.182) дают соответствующие веса для университетов А, В и С с точки зрения академической репутации. Аналогично величины (wia, wlb, wlc) = (0.129, 0.277, 0.594) являются относительными весами, касающимися местонахождения университетов.
Согласованность матрицы сравнений. В примере 3.2-2 мы отмечали, что все столбцы нормализованных матриц N и NR идентичны, а столбцы матрицы NL таковыми не являются. Одинаковые столбцы указывают на то, что результирующие относительные веса сохраняют одно и то же значение независимо от того, как выполняется сравнение. В этом случае говорят, что исходные матрицы сравнения А и АR являются согласованными. Следовательно, матрица АL, не является таковой.
Согласованность означает, что решение будет согласовано с определениями парных сравнений критериев или альтернатив. С математической точки зрения согласованность матрицы А означает, что аij аjk = aik для всех i, j и k. Например, в матрице AR из примера 3.2-2 а13 = 3 и
а12 а23 = 2 х 3/2 = 3. Свойство согласованности требует линейной зависимости столбцов (и строк) матрицы А. В частности, столбцы любой матрицы сравнений размерностью 2x2 являются зависимыми, и, следовательно, такая матрица всегда является согласованной. Не все матрицы сравнений являются согласованными. Действительно, принимая во внимание, что такие матрицы строятся на основе человеческих суждений, можно ожидать некоторую степень несогласованности, и к ней следует относиться терпимо при условии, что она не выходит за определенные "допустимые" рамки.
Чтобы выяснить, является ли уровень согласованности "допустимым", необходимо определить соответствующую количественную меру для матрицы сравнений А. В примере 3.2-2 мы видели, что идеально согласованная матрица А порождает нормализованную матрицу N, в которой все столбцы одинаковы.
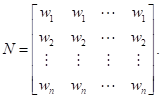
Отсюда следует, что матрица сравнений А может быть получена из матрицы N путем деления элементов i-го столбца на wi - (это процесс, обратный к нахождению матрицы N из А). Итак, получаем следующее.
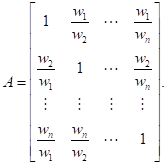
Используя приведенное определение матрицы А, имеем
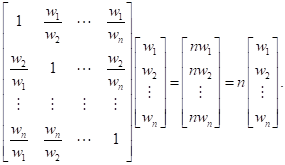
В компактной форме условие согласованности матрицы А формулируется следующим образом. Матрица А будет согласованной тогда и только тогда, когда
Aw = nw,
где w – вектор-столбец относительных весов wi , i= 1, 2,..., n.
Когда матрица А не является согласованной, относительный вес wi аппроксимируется средним значением n элементов i-й строки нормализованной матрицы N (см. пример 3.2-2). Обозначив через w вычисленную оценку (среднее значение), можно показать, что
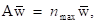
где nmах ³ n. В этом случае, чем ближе nmах к n, тем более согласованной является матрица сравнения А. В результате в соответствии с методом анализа иерархий вычисляется коэффициент согласованности в виде
 ,
,
где,
 , коэффициент согласованности матрицы А,
, коэффициент согласованности матрицы А,
 , стохастический коэффициент согласованности матрицы А.
, стохастический коэффициент согласованности матрицы А.
Стохастический коэффициент согласованности RI определяется эмпирическим путем как среднее значение коэффициента CI для большой выборки генерированных случайным образом матриц сравнения А.
Коэффициент согласованности CR используется для проверки согласованности матрицы сравнения А следующим образом. Если CR < 0.1, уровень несогласованности является приемлемым. В противном случае уровень несогласованности матрицы сравнения А является высоким и лицу, принимающему решение, рекомендуется проверить элементы парного сравнения aij матрицы А в целях получения более согласованной матрицы.
Значение nmах вычисляется на основе матричного уравнения 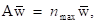 при этом нетрудно заметить, что i'-е уравнение этой системы имеет вид:
при этом нетрудно заметить, что i'-е уравнение этой системы имеет вид:
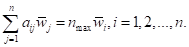
Поскольку  , легко проверить, что
, легко проверить, что
 .
.
Это значит, что величину nmах можно определить путем вычисления вектор-столбца  с последующим суммированием его элементов.
с последующим суммированием его элементов.
Пример 3.2-3
В примере 3.2-2 матрица AL является несогласованной, так как столбцы матрицы NL неодинаковы. Требуется исследовать согласованность матрицы АL,.
Вычислим значение nmax. Из данных примера 3.2-2 имеем
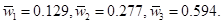
Следовательно,
 .
.
Отсюда получаем
 .
.
Следовательно, для n = 3 имеем
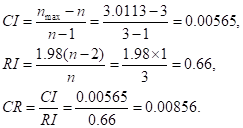
Так как CR<0.1, уровень несогласованности матрицы AL является приемлемым.
3.2.3. Упражнения 3.2, b
1. Отдел кадров фирмы сузил поиск будущего сотрудника до трех кандидатур: Стив (S), Джейн (J) и Майса (М). Конечный отбор основан на трех критериях: собеседование (С), опыт работы (О) и рекомендации (Р). Отдел кадров использует матрицу А (приведенную ниже) для сравнения трех критериев. После проведенного собеседования с тремя претендентами, сбора данных, относящихся к опыту их работы и рекомендациям, построены матрицы Ас, Ао и Ар. Какого из трех кандидатов следует принять на работу? Оцените согласованность данных.

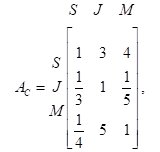

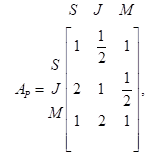
2. Кевин и Джун Парки (К и Д) покупают новый дом. Рассматриваются три варианта А, В и С. Парки согласовали два критерия для выбора дома: площадь зеленой лужайки (Л) и близость к месту работы (Б), а также разработали матрицы сравнений, приведенные ниже. Необходимо оценить три дома в порядке их приоритета и вычислить коэффициент согласованности каждой матрицы.


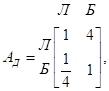

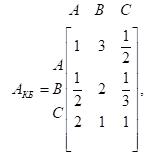

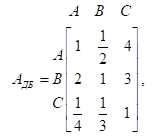
3. Автор книги по исследованию операций определил три критерия для выбора издательства, которое будет печатать его книгу: процент авторского гонорара (R), уровень маркетинга (М) и размер аванса (А). Издательства N и Р проявили интерес к изданию книги. Используя приведенные ниже матрицы сравнения, необходимо дать оценку двум издательствам и оценить согласованность решения.



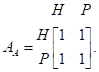
4. Профессор политологии планирует предсказать исход выборов в местный школьный совет. Кандидаты I, В и S баллотируются на одно место. Профессор делит всех избирателей на три категории: левые (L), центристы (C) и правые (R). Оценка кандидатов основывается на трех факторах: педагогический опыт (О), отношение к детям (Д) и характер (X). Ниже приведены матрицы сравнения для первого иерархического уровня, связанного с градацией избирателей (левые, центристы и правые).

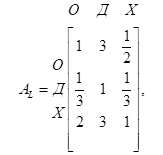

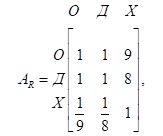
Профессор сгенерировал еще девять матриц сравнения для трех кандидатов на втором иерархическом уровне, связанном с педагогическим опытом, отношением к детям и характером. Затем был использован метод анализа иерархий для сведения этих матриц к следующим относительным весам.
| Кандидат | Левые | Центристы | Правые | ||||||
| О | Д | Х | О | Д | Х | О | Д | Х | |
| I | 0.1 | 0.2 | 0.3 | 0.3 | 0.5 | 0.2 | 0.7 | 0.1 | 0.3 |
| B | 0.5 | 0.4 | 0.2 | 0.4 | 0.2 | 0.4 | 0.1 | 0.4 | 0.2 |
| S | 0.4 | 0.4 | 0.5 | 0.3 | 0.3 | 0.4 | 0.2 | 0.5 | 0.5 |
Используя эту информацию, необходимо определить, кто из кандидатов выиграет выборы, и оценить согласованность решения.
5. Школьный округ крайне заинтересован в сокращении своих расходов, что вызвано очередным уменьшением бюджетного финансирования начальных школ. Есть две возможности решить эту проблему: ликвидировать программу физического воспитания (Ф) или программу музыкального образования (М). Управляющий округа сформировал комитет с равным представительством от местного школьного совета (С) и ассоциации родителей и учителей (Р) для изучения ситуации и вырботки предложения. Комитет принял решение изучить ситуацию с точки зрения ограничения бюджета (Б) и потребностей учеников (П). Проведенный анализ дал следующие матрицы сравнения.

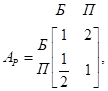

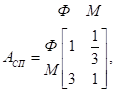

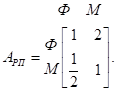
Требуется проанализировать ситуацию, связанную с принятием решения, и выработать соответствующее предложение.
6. Решив купить автомобиль, человек сузил свой выбор до трех моделей: М1, М2 и М3. Факторами влияющими на его решение , являются: стоимость автомобиля (С), стоимость обслуживания (О), стоимость поездки по городу (Г) и сельской местности (М). Следующая таблица содержит необходимые данные, соответствующие трехгодичному сроку эксплуатации автомобиля.
| Модель автомобиля | С ($) | О ($) | Г ($) | М ($) |
| Ml | 6 000 | 1 800 | 4 500 | 1 500 |
| М2 | 8 000 | 1 200 | 2 250 | 750 |
| М3 | 10 000 | 600 | 1 125 | 600 |
Используйте указанные стоимости для построения матриц сравнений. Оцените согласованность матриц и определите модель автомобиля, которую следует выбрать.
3.3. Принятие решений в условиях риска
Если решение принимается в условиях риска, то стоимости альтернативных решений обычно описываются вероятностными распределениями. По этой причине принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат. Такой подход имеет свои недостатки, которые не позволяют использовать его в некоторых ситуациях. Для них разработаны модификации упомянутого критерия. В этой главе рассматриваются часто используемые подходы к принятию решений в условиях риска.
3.3.1. Критерий ожидаемого значения
Критерий ожидаемого значения сводится либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что прибыль (затраты), связанная с каждым альтернативным решением, является случайной величиной.
ДЕРЕВО РЕШЕНИЙ. В приведенном ниже примере рассматривается простая ситуация, связанная с принятием решения при наличии конечного числа альтернатив и точных значений матрицы доходов.
Пример 3.3-1
Предположим, что вы хотите вложить на фондовой бирже 10 000 долларов в акции одной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20%. Компания В обеспечивает безопасность инвестиций с 15% прибыли в условиях повышения котировок на бирже и только 5% – в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60% прогнозируют повышение котировок и с вероятностью 40% – понижение котировок. В какую компанию следует вложить деньги?
Информация, связанная с принятием решения, суммирована в следующей таблице.
| Альтернативное решение | Прибыль от инвестиции за один год | |
| При повышении котировок ($) | При понижении котировок ($) | |
| Акции компании А | 5 000 | – 2 000 |
| Акции компании В | 1 500 | 500 |
| Вероятность события | 0.6 | 0.4 |
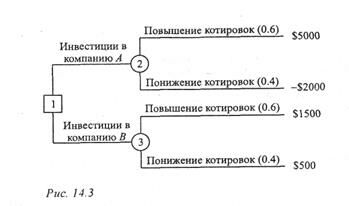
Эта задача может быть также представлена в виде дерева решений, показанного на рис. 14.3. На этом рисунке используется два типа вершин: квадратик представляет "решающую" вершину, а кружок – "случайную". Таким образом, из вершины 1 ("решающая") выходят две ветви, представляющие альтернативы, связанные с покупкой акций компании А или В. Далее две ветви, выходящие из "случайных" вершин 2 и 3, соответствуют случаям повышения и понижения котировок на бирже с вероятностями их появления и соответствующими платежами.
Исходя из схемы рис. 14.3, получаем ожидаемую прибыль за год для каждой из двух альтернатив.
Для акций компании А: $5 000 х 0.6 + (-2000) х 0.4 = S2 200.
Для акций компании В: $1 500 х 0.6 + $500 х 0.4 = $1 100.
Вашим решением, основанным на этих вычислениях, является покупка акций компании А.
В теории принятия решений повышение и понижение котировок на бирже именуются состояниями природы, возможные реализации которых являются случайными событиями (в данном случае с вероятностями 0.6 и 0.4). В общем случае задача принятия решений может включать п состояний природы и т альтернатив. Если pj – вероятность j-го состояния природы, a aij – платеж, связанный с принятием решения i при состоянии природы j (i = 1, 2, ..., m, j = 1, 2, ..., п), тогда ожидаемый платеж для решения i вычисляется в виде
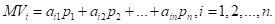
где по определению р1 + р2 + ...+ рn = 1.
Наилучшим решением будет то, которое соответствует  или
или  , в зависимости от того, является ли платеж в задаче доходом (прибылью) или убытком (затратами).
, в зависимости от того, является ли платеж в задаче доходом (прибылью) или убытком (затратами).
Упражнения 3.3,а
1. Вас пригласили на телевизионную игру Колесо фортуны. Колесо управляется электронным образом с помощью двух кнопок, которые сообщают колесу сильное (В) или слабое (Я) вращение. Само колесо разделено на равные области – белую (Б) и красную (К). Вам сообщили, что в белой области колесо останавливается с вероятностью 0.3, а в красной – 0.7. Плата, которую вы получаете за игру, равна (в долларах) следующему.

Изобразите соответствующее дерево решений.
2. Фермер Мак-Кой может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0.25, 0.30 и 0.45. Если цены возрастут, урожай кукурузы даст 30 000 долларов чистого дохода, а урожай соевых бобов – 10 000 долларов. Если цены останутся неизменными, Мак-Кой лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35 000 и 5 000 долларов соответственно.
a) Представьте данную задачу в виде дерева решений.
b) Какую культуру следует выращивать Мак-Кою?
3. Допустим, у вас имеется возможность вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиции может измениться в зависимости от условий рынка. Существует вероятность 10 %, что ситуация на рынке ценных бумаг ухудшится, 50 % – что рынок останется умеренным и 40 % – рынок будет возрастать. Следующая таблица содержит значения процентов прибыли от суммы инвестиции при трех возможностях развития рынка.
| Альтернатива (фонды) | Процент прибыли от инвестиции (%) | ||
| Ухудшающийся рынок | Умеренный рынок | Растущий рынок | |
| Простой | +5 | +7 | +8 |
| Специальный | -10 | +5 | +30 |
| Глобальный | +2 | +7 | +20 |
a) Представьте задачу в виде дерева решений.
b) Какой фонд открытого типа вам следует выбрать?
4. Предположим, у вас имеется возможность вложить деньги либо в 7.5%-ные облигации, которые продаются по номинальной цене, либо в специальный фонд, который выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастет до 8%, и в этом случае номинальная стоимость облигаций увеличится на 10%, а цена акций фонда – на 20%. Если прогнозируется " спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда увеличится на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% – наступление спада. Ваше решение относительно инвестиций принимается с учетом экономических условий следующего года.
a) Представьте задачу в виде дерева решений.
b) Будете ли вы покупать акции фонда или облигации?
5. Фирма планирует производство новой продукции быстрого питания в национальном масштабе. Исследовательский отдел убежден в большом успехе новой продукции и хочет внедрить ее немедленно, без рекламной кампании на рынках сбыта фирмы. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную кампанию. Такая кампания обойдется в 100000 долларов, а в случае успеха принесет 950 000 долларов годового дохода. В случае неуспеха рекламной кампании (вероятность этого составляет 30 %) годовой доход оценивается лишь в 200000 долларов. Если рекламная кампания не проводится вовсе, годовой доход оценивается в 400 000 долларов при условии, что покупателям понравится новая продукция (вероятность этого равна 0.8), и в 200 000 долларов с вероятностью 0.2, если покупатели останутся равнодушными к новой продукции.
a) Постройте соответствующее дерево решений.
b) Как должна поступить фирма в связи с производством новой продукции?
6. Симметричная монета подбрасывается три раза. Вы получаете один доллар за каждое выпадение герба (Г) и дополнительно 0.25 доллара за каждые два последовательных выпадения герба (заметим, что выпадение ГГГ состоит из двух последовательностей /Т). Однако Вам приходится платить 1.1 доллара за каждое выпадение решетки (Р). Вашим решением является участие или неучастие в игре.
a) Постройте соответствующее дерево решений для описанной игры.
b) Будете ли вы играть в эту игру?
7. Предположим, у вас имеется возможность сыграть в игру следующего содержания. Симметричная игральная кость бросается два раза, при этом возможны четыре исхода: 1) выпадает два четных числа, 2) выпадает два нечетных числа, 3) выпадает сначала четное, затем нечетное число, 4) выпадает сначала нечетное, затем четное число. Вы можете делать одинаковые ставки на два исхода. Например, вы можете поставить на два четных числа (исход 1) и два нечетных (исход 2). Выигрыш на каждый доллар, поставленный на первый исход, равен 2 доллара, на второй и третий исходы – 1.95 доллара, на четвертый – 1.50 доллара.
a) Постройте дерево решений для описанной игры.
b) На какие исходы следует делать ставки?
c) Можно ли иметь стабильный выигрыш в этой игре?
8. Фирма производит партии продукции с 0.8 %, 1 %, 1.2 % и 1.4 % бракованных изделий с вероятностями 0.4, 0.3, 0.25 и 0.05 соответственно. Три потребителя А, В и С заключили контракт на получение партий изделий с процентом некачественных изделий не выше 0.8 %, 1.2 % и 1.4 % соответственно. Фирма штрафуется в сумме 1000 долларов за каждый пункт процента[1] в случае, когда процент некачественных изделий выше указанного. Наоборот, поставка партий изделий с меньшим процентом бракованных изделий, чем оговорено в контракте, приносит фирме прибыль в 500 долларов за каждый пункт процента. Предполагается, что партии изделий перед отправкой не проверяются.
a) Постройте соответствующее дерево решений.
b) Какой из потребителей должен иметь наивысший приоритет при получении своего заказа?
9. Фирма планирует открыть новое предприятие в Арканзасе. В настоящее время имеется возможность построить либо крупное предприятие, либо небольшое, которое через два года можно будет расширить при условии высокого спроса на выпускаемую им продукцию. Рассматривается задача принятия решений на десятилетний период. Фирма оценивает, что на протяжении этих 10 лет вероятность высокого и низкого спроса на производимую продукцию будет равна 0.75 и 0.25 соответственно. Стоимость немедленного строительства крупного предприятия равна 5 миллионов долларов, а небольшого – один миллион долларов. Расширение малого предприятия через два года обойдется фирме в 4.2 миллиона долларов. Прибыль, получаемая от функционирования производственных мощностей на протяжении 10 лет, приводится в следующей таблице.
| Альтернатива | ||
| Высокий спрос | Низкий спрос | |
| Крупное предприятие сейчас | 1000 | 300 |
| Небольшое предприятие сейчас | 250 | 200 |
| Расширенное предприятие через 2 года | 900 | 200 |
a) Постройте соответствующее дерево решений, принимая во внимание, что через два года фирма может либо расширить небольшое предприятие, либо не расширять его.
b) Сформулируйте стратегию строительства для фирмы на планируемый 10-летний период. (Для простоты не принимайте во внимание возможную инфляцию.)
10. Решите предыдущее упражнение в предположении, что ежегодная учетная ставка равна 10 % и что решение принимается с учетом инфляции. (Совет. Для решения задачи необходимы таблицы сложных процентных ставок.)
11. Решите упражнение 9 в предположении, что спрос может быть высоким, средним и низким с вероятностями 0.7, 0.2 и 0.1 соответственно. Расширение небольшого предприятия будет проведено лишь в том случае, если на протяжении первых двух лет спрос будет высоким. Следующая таблица содержит данные о прибылях за год.
| Альтернатива | Ожидаемый доход за год (тысячи долл.) | ||
| Высокий спрос | Средний спрос | Низкий спрос | |
| Крупное предприятие сейчас | 1000 | 500 | 300 |
| Небольшое предприятие сейчас | 400 | 280 | 150 |
| Расширенное предприятие через 2 года | 900 | 600 | 200 |
Более сложные ситуации выбора решений. Для демонстрации других возможностей применения критерия ожидаемого значения рассмотрим ситуации принятия решений, в которых плата является математической функцией альтернативных решений. В этом случае представление задачи в виде дерева решений хотя и является возможным, но может быть не столь полезным, как в предыдущих примерах.
Пример 3.3-2
Электроэнергетическая компания использует парк из 20 грузовых автомобилей для обслуживания электрической сети. Компания планирует периодический профилактический ремонт автомобилей. Вероятность рt поломки автомобиля по истечении t месяцев после профилактического ремонта оценивается следующим образом.
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ³ 10 |
| рt | 0.05 | 0.07 | 0.10 | 0.13 | 0.18 | 0.23 | 0.33 | 0.43 | 0.50 | 0.55 |
Случайная поломка одного грузового автомобиля обходится компании в 200 долларов, а планируемый профилактический ремонт в 50 долларов. Необходимо определить оптимальный период (в месяцах) между планируемыми профилактическими ремонтами.
Обозначим через N искомое число месяцев между профилактическими ремонтами. На протяжении N-месячного цикла могут иметь место два вида расходов: 1) затраты, связанные с устранением поломки автомобиля на протяжении первых N – 1 месяцев и 2) затраты на профилактический ремонт в конце цикла. Затраты второго вида (профилактический ремонт) составляют $50 х 20 автомобилей, т.е. 1000 долларов на цикл. Затраты, связанные с устранением поломок автомобилей, должны основываться на среднем количестве автомобилей, вышедших из строя на протяжении первых N - 1 месяцев цикла. Здесь мы имеем два состояния по истечении месяца t: поломка автомобиля с вероятностью рt и ее отсутствие с вероятностью 1 – рt. Следовательно, ожидаемое число поломок по истечении месяца t равно количеству автомашин в парке, умноженному на рt т.е. 20рt. Используя этот результат, подсчитаем ожидаемое общее число сломавшихся автомобилей на протяжении первых N – 1 месяцев цикла в виде суммы соответствующих величин для каждого месяца в отдельности, т.е. 20p1 + 20р2 + ... + 20pN – 1 = 20(р1 +р2 + ... +pn – 1). Обозначив через EC(N) общую ожидаемую стоимость для цикла между профилактическими ремонтами, имеем следующее.
EC(N) = $1000 + $200 х 20(р1 +р2 + ... +pn – 1).
Задача выбора решения компанией сводится таким образом к определению длины цикла N, которая минимизирует общие ожидаемые затраты за один месяц ECPM(N), т.е. величину
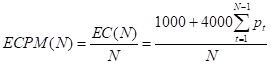
Минимизацию функции ECPM(N) нельзя выполнить в явной форме. Вместо этого используется следующая табличная форма нахождения решения.
| Оптимальное N ® | N | pN |
| ECPM(N) |
| 1 | 0.05 | 0.00 | $ 1 000.00 | |
| 2 | 0.07 | 0.05 | 600.00 | |
| 3 | 0.10 | 0.12 | 493.33 | |
| 4 | 0.13 | 0.22 | 470.00 | |
| 5 | 0.18 | 0.35 | 480.00 | |
| 6 | 0.23 | 0.53 | 520.00 |
Вычисления показывают, что ECPM(N) достигает своего минимума при N = 4. Следовательно, профилактический ремонт автомобилей нужно выполнять каждые четыре месяца.
Задачу выбора решения в примере 3.3-2 можно также представить в виде дерева решений. Вам предлагается сделать это в упражнении 3.3,b(1).
Упражнения 3.3,b
1. В задаче из примера 3.3-2 стоимость профилактического ремонта одного автомобиля равна 75 долларов, а стоимость устранения поломки – 200 долларов. Вероятность поломки автомобиля в первый месяц равна 0.03 и увеличивается на 0.01 для каждого последующего месяца, по десятый включительно. Начиная с одиннадцатого месяца и далее, вероятность поломки сохраняется постоянной на уровне 0.13.
a) Постройте соответствующее дерево решений.
b) Определите оптимальную длину цикла для профилактического ремонта.
2. Ежедневный спрос на булочки в продовольственном магазине задается следующим распределением вероятностей.
| N | 100 | 150 | 200 | 250 | 300 |
| Рn | 0.20 | 0.25 | 0.30 | 0.15 | 0.10 |
Магазин покупает булочку по 55 центов, а продает по 1.20 доллара. Если булочка не продана в тот же день, то к концу дня она может быть реализована за 25 центов. Величина запаса булочек может принимать одно из возможных значений спроса, которые перечислены выше.
a) Постройте соответствующее дерево решений.
b) Сколько булочек необходимо заказывать ежедневно?
3. Пусть в предыдущем упражнении временной интервал, для которого необходимо решить задачу принятия решений, составляет два дня. Альтернативы для второго дня зависят от объема реализации булочек в первый день. Если реализован в точности весь запас первого дня, магазин закажет такое же количество булочек и на второй день. Если потребность в булочках в первый день превышает имеющийся запас, то для второго дня магазин может заказать любой из объемов спроса на булочки, который превышает запас первого дня. И, наконец, если в первый день реализовано меньше булочек, чем было закуплено, то для второго дня магазин может заказать любой из объемов спроса на булочки, который меньше запаса первого дня. Постройте соответствующее дерево решений и определите оптимальную стратегию заказа.
4. Автомат производит, α тысяч единиц некоего продукта ежедневно. Если α увеличивается, доля брака р, будучи случайной величиной, возрастает в соответствии со следующей функцией плотности распределения:
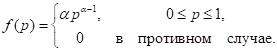
Каждое бракованное изделие приносит убыток в 50 долларов, а качественное изделие — прибыль в 5 долларов.
a) Объясните, почему трудно построить дерево решений для этой задачи.
b) Определите значение а, при котором ожидаемая прибыль принимает максимальное значение.
5. Наружный диаметр d цилиндра, производимого автоматом, имеет верхнее и нижнее допустимые значения d + tU и d - tL соответственно. Производственный процесс настроен так, что величина диаметра является нормально распределенной случайной величиной с математическим ожиданием μ и стандартным отклонением σ. Каждый цилиндр со значением диаметра, превышающим верхнее допустимое значение, доводится до нужных размеров за с1 долларов. Цилиндр, диаметр которого меньше установленной нижней нормы, реализуется с убытком с2 долларов. Определите оптимальное значение настройки для автомата.
6. В производственном процессе периодически производится заточка режущих инструментов. Если инструмент не затачивается достаточно часто, то возрастает процент брака, и наоборот. Пусть SU и SL – соответственно верхний и нижний допустимые пределы измеримого размера изделия, обрабатываемого с помощью режущего инструмента в данном производственном процессе. Далее пусть μ(t) – среднее значение результата производственного процесса (например, размера изделия, получаемого в результате обработки режущим инструментом) после того, как прошло t единиц времени после последней заточки инструмента; здесь  соответствует идеальной начальной настройке инструмента. Стоимость заточки инструмента равна с1, а стоимость бракованного изделия — с2. Продукция производится партиями объемом Q со скоростью r единиц продукции в единицу времени, и результат процесса описывается нормальным распределением со средним значением μ(t) и не зависящим от времени стандартным отклонением
соответствует идеальной начальной настройке инструмента. Стоимость заточки инструмента равна с1, а стоимость бракованного изделия — с2. Продукция производится партиями объемом Q со скоростью r единиц продукции в единицу времени, и результат процесса описывается нормальным распределением со средним значением μ(t) и не зависящим от времени стандартным отклонением  .
.
a) Найдите выражение для ожидаемой стоимости заточки инструмента и переделки дефектных изделий как функцию интервала времени Т между последовательными заточками.
b) Покажите, что оптимальное значение Т не зависит от Q, и объясните это.
c) Найдите численное значение Т при следующих данных: с1 = 10 долларов, с2 - 48.85 долларов, r = 10 единиц продукции за час, и
и  .
.
(Совет. Аппроксимируйте число заточек инструмента при изготовлении партии объемом Q с помощью числа  . Кроме того, используйте численное интегрирование для нахождения оптимального значения Т.)
. Кроме того, используйте численное интегрирование для нахождения оптимального значения Т.)
1. Критерий предельного уровня. Фирма для технических целей использует в одном из своих производственных процессов химические препараты (химикалии). Срок годности этих препаратов составляет один месяц, после чего оставшаяся их часть уничтожается. Объем используемых фирмой химических препаратов (в галлонах) является случайной величиной, изменяющейся в соответствии со следующим распределением.
Реально химикалии используются на протяжении месяца в соответствии с равномерным распределением. Фирма планирует определить количество химических препаратов, удовлетворяющих двум конфликтующим критериям (или предельным уровням).
1) Среднее число оставшихся химикалий не превышает 20 галлонов в месяц.
2) Среднее количество недостающих химикалий не превышает 40 галлонов в месяц.
3.3.2. Другие критерии ожидаемого значения
В этом разделе рассматриваются три модификации критерия ожидаемого значения. Первая состоит в определении апостериорных вероятностей на основе эксперимента над исследуемой системой, вторая — в полезности реальной стоимости денег, а третья модифицирует критерий ожидаемого значения таким образом, что он может быть использован для принятия решений при краткосрочном планировании.
АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ байеса. Распределения вероятностей, которые используются при формулировке критерия ожидаемого значения, получаются, как правило, из накопленной ранее информации. В некоторых случаях оказывается возможным модифицировать эти вероятности с помощью текущей и/или полученной ранее информации, которая обычно основывается на исследовании выборочных (или экспериментальных) данных. Получаемые при этом вероятности называют апостериорными (или Байесовскими), в отличие от априорных, полученных из исходной информации. Следующий пример показывает, как рассмотренный в разделе 3.3.1 критерий ожидаемого значения можно модифицировать так, чтобы воспользоваться новой информацией, содержащейся в апостериорных вероятностях.
Пример 3.3-3
В примере 3.3-1 априорные вероятности 0.6 и 0.4 повышения и понижения котировок акций на бирже были определены из наличных публикаций финансового характера. Предположим, вместо того чтобы полностью полагаться на эти публикации, вы решили провести личное исследование путем консультаций с другом, который хорошо разбирается в вопросах, касающихся фондовой биржи. Друг высказывает общее мнение "за" или "против" инвестиций. Это мнение в дальнейшем определяется количественно следующим образом. При повышении котировок его мнение с 90 %-ной вероятностью будет "за", при снижении котировок вероятность его мнения "за" уменьшится до 50 %. Каким образом можно извлечь пользу из этой дополнительной информации?
Мнение друга фактически представляет условные вероятности "за - против" при заданных состояниях природы в виде повышения и понижения котировок. Введем следующие обозначения:
 — мнение "за",
— мнение "за",
 — мнение "против",
— мнение "против",
 — повышение котировок,
— повышение котировок,
 — понижение котировок.
— понижение котировок.
Мнение друга можно записать в виде вероятностных соотношений следующим образом.

 ,
,
 ,
, 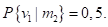
С помощью этой дополнительной информации задачу выбора решения можно сформулировать следующим образом.
1. Если мнение друга "за", акции какой компании следует покупать – А или В?
2. Если мнение друга "против", то, опять-таки, – акции какой компании следует покупать – А или В?
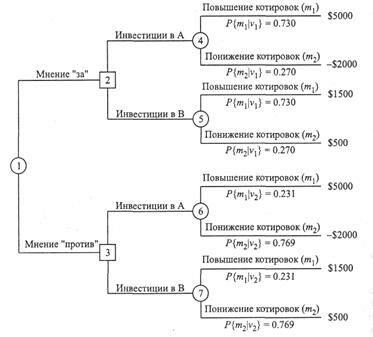
рис. 14.3.
Рассматриваемую задачу можно представить в виде дерева решений, показанного на рис. 14.4. Узлу 1 здесь соответствует случайное событие, мнение друга, с I соответствующими вероятностями "за" и "против". Узлы 2 и 3 представляют выбор между компаниями А и В при известном мнении друга "за" или "против" со- I ответственно. Узлы 4-7 соответствуют случайным событиям, связанным с повышением и понижением котировок.
Для оценки различных альтернатив, показанных на рис. 14.4, необходимо вычислить апостериорные вероятности  , указанные на соответствующих ветвях, выходящих из узлов 4-7. Эти апостериорные вероятности вычисляются с учетом дополнительной информации, содержащейся в рекомендациях друга, с помощью следующих действий.
, указанные на соответствующих ветвях, выходящих из узлов 4-7. Эти апостериорные вероятности вычисляются с учетом дополнительной информации, содержащейся в рекомендациях друга, с помощью следующих действий.
Шаг 1. Условные вероятности  для данной задачи запишем следующим образом.
для данной задачи запишем следующим образом.
|
|
| v1 | v2 |
| m1 | 0.9 | 0.1 | |
| m2 | 0.5 | 0.5 |
Шаг 2. Вычисляем вероятности совместного появления событий.
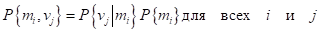
При заданных априорных вероятностях Р{т1] = 0.6 и Р{т2} = 0.4 вероятности совместного появления событий определяются умножением первой и второй строк таблицы, полученной на шаге 1, на 0.6 и 0.4 соответственно. В результате имеем следующее.
|
|
| v1 | v2 |
| m1 | 0.54 | 0.06 | |
| m2 | 0.20 | 0.20 |
Сумма всех элементов этой таблицы равна 1.
Шаг 3. Вычисляем абсолютные вероятности.
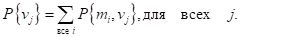
Эти вероятности получаются путем суммирования элементов соответствующих столбцов таблицы, полученной на шаге 2. В итоге имеем следующее.
Шаг 4. Определяем искомые апостериорные вероятности по формуле
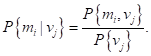
Эти вероятности вычисляются в результате деления каждого столбца таблицы, полученной на шаге 2, на элемент соответствующего столбца таблицы, вычисленной на шаге 3, что приводит к следующим результатам (округленным до трех десятичных знаков).
|
|
| v1 | v2 |
| m1 | 0.730 | 0.231 | |
| m2 | 0.270 | 0.769 |
Это те вероятности, которые показаны на рис. 14.4. Они отличаются от исходных априорных вероятностей Р{m1} = 0.6 и Р{т2] = 0.4.
Теперь можно оценить альтернативные решения, основанные на ожидаемых платежах для узлов 4-7.
Мнение "за"
Доход от акций компании А в узле 4 = 5000 х 0.730 + (-2000) х 0.270 = $3110.
Доход от акций компании В в узле 5 = 1500 х 0.730 + 500 х 0.270 = $1230.
Решение. Инвестировать в акции компании А.
Мнение "против"
Доход от акций компании А в узле 6 = 5000 х 0.231 + (-2000) х 0.769 = -$383.
Доход от акций компании В в узле 7 = 1500 х 0.231 + 500 х 0.769 = $731.
Решение. Инвестировать в акции компании В.
Заметим, что предыдущие решения эквивалентны утверждению, что ожидаемые платы в узлах 2 и 3 равны 3110 и 731 доллар соответственно (рис. 14.4). Следовательно, при известных вероятностях P{v1} = 0.74 и P{v2} = 0.26, вычисленных на шаге 3, можно вычислить ожидаемую плату для всего дерева решений (упр. 14.3,с(3)).
Упражнения 3.3,с
1. Несмотря на сезон дождей, Джим Боб планирует завтра идти на рыбалку, но только если не будет дождя. Из данных о погоде прошлых лет следует, что имеется 70 %-ная вероятность, что в сезон дождей будет идти дождь. В шесть часов вечера синоптики предсказали с 85 %-ной вероятностью, что завтра будет дождь. Следует ли Джиму Бобу планировать рыбалку на завтра?
2. Фирма Электра получает 75 % электронных деталей от поставщика А и 25 % – от поставщика В. Доля брака в продукции поставщиков А и В составляет 1 % и 2 % соответственно. При проверке пяти деталей из полученной партии обнаружена лишь одна дефектная. Определите вероятность того, что партия получена от поставщика А. Проведите аналогичные вычисления относительно поставщика В. (Подсказка. Вероятность появления бракованной детали в партии подчиняется биномиальному закону распределения.)
3. Предположим, что в задаче из примера 3.3-3 есть дополнительный выбор, связанный с инвестированием 10 000 долларов в надежный депозит, который приносит 8 % прибыли. Совет вашего друга, по-прежнему, относится к инвестированию через биржу.
a) Постройте соответствующее дерево решений.
b) Какое оптимальное решение в этом случае? (Совет. Используйте вероятности p{v1} и P{v2}, полученные на шаге 3 в примере 3.3-3, для вычисления ожидаемой суммы инвестирования через биржу.)
4. Допустим, вы являетесь автором романа, который обещает быть популярным. У вас имеется возможность либо самостоятельно напечатать роман, либо через издательство. Издательство предлагает вам 20 000 долларов за подписание контракта. Если роман будет пользоваться спросом, будет продано 200 000 экземпляров, в противном случае – лишь 10 000 экземпляров. Издательство выплачивает авторский гонорар в сумме один доллар за экземпляр. Исследование рынка, проведенное издательством, свидетельствует о том, что существует 70 %-ная вероятность, что роман будет популярным. Если же вы сами напечатаете роман, то понесете потери в сумме 90 000 долларов, связанные с печатанием и маркетингом, но в этом случае каждый проданный экземпляр принесет вам прибыль в два доллара.
a) Принимая во внимание имеющуюся информацию, примете ли вы предложение издательства или будете печатать роман самостоятельно?
b) Предположим, что вы заключили договор с литературным агентом на исследование, связанное с потенциальным успехом романа. Исходя из предыдущего опыта, компания извещает вас, что если роман будет пользоваться спросом, то исследование предскажет неверный результат в 20 % случаев. Если же роман будет не популярен, то исследование предскажет верный результат в 85 % случаев. Как эта информация повлияет на ваше решение?
5. Вернитесь к проблеме выбора решения фермером Мак Коем из упр. 3.3,а(2). Фермер имеет дополнительный выбор, связанный с использованием земли как пастбища, что гарантированно принесет ему прибыль в 7500 долларов. Фермер получил также дополнительную информацию от брокера, касающуюся степени стабильности будущих цен на продукцию. Оценки брокера "благоприятный — неблагоприятный" затем выражаются количественно в виде следующих условных вероятностей.
|
|
| a1 | a2 |
| s1 | 0.15 | 0.85 | |
| s2 | 0.50 | 0.50 | |
| s3 | 0.85 | 0.15 |
В данном случае а1 и а2 – оценки брокера "благоприятный" и "неблагоприятный", a s1 s2 и s3 представляют изменение в будущих ценах: соответственно "понижение", "такие же", "повышение".
a) Постройте соответствующее дерево решений.
b) Найдите оптимальное решение задачи.
6. Пусть в упр. 3.3,а(5) дирекция компании решила провести пробную продажу своей продукции в выбранных населенных пунктах. Результатом пробной продажи являются оценки "хорошо" (а1) или "плохо" (а2). Тест дает следующие условные вероятности с проведением рекламной кампании и без нее.
|
|
|
| ||||||
|
| a1 | a2 |
|
| a1 | a2 | ||
| v1 | 0.95 | 0.05 | w1 | 0.8 | 0.2 | |||
| v2 | 0.3 | 0.7 | w2 | 0.4 | 0.6 | |||
Здесь символы v1 и v2 обозначают, соответственно, "успех" и "неуспех", a w1 и w2 – "восприимчивый" и "невосприимчивый" покупатель.
a) Постройте соответствующее дерево решений.
b) Определите оптимальный план действий фирмы.
7. Статистические данные о работе компании показывают, что с вероятностью 5 % произведенная партия продукции будет неприемлемой (плохой). Плохая партия содержит 15 % дефектных изделий, а хорошая – лишь 4 %. Пусть значение переменной а = а1 (= а2) обозначает, что партия изделий является хорошей (плохой). Тогда соответствующие априорные вероятности равны соответственно P{a = a1} = 0.95 P{a = a2}=0.05.
Вместо того чтобы отправить партии продукции с характеристиками, основанными на априорных вероятностях, из каждой партии проверяются два изделия. Возможны следующие результаты проверки.
Оба изделия являются доброкачественными (s1).
Одно изделие является доброкачественным (s2).
Оба изделия являются бракованными (s3).
a) Определите апостериорные вероятности  .
.
b) Предположим, что фирма отправляет партии продукции двум потребителям А и В. Контракты с ними определяют, что процент бракованных изделий в поставках не должен превышать 5 % и 8 % соответственно. Предусматривается штраф в 100 долларов за превышение на один процент максимально допустимого лимита бракованных изделий. Поставка партий лучшего качества, чем указано в контракте, приносит производителю прибыль в 80 долларов за каждый процент уменьшения доли бракованных изделий. Постройте соответствующее дерево решений и определите приоритетную стратегию отправки партий продукции.
ФУНКЦИИ ПОЛЕЗНОСТИ. В предыдущих примерах критерий ожидаемого значения применялся лишь в тех ситуациях, где платежи выражались в виде реальных денег. Имеются многочисленные случаи, когда при анализе следует использовать скорее полезность, чем реальную величину платежей. Для демонстрации этого предположим, что имеется шанс 50 на 50, что инвестиция в 20 000 долларов или принесет прибыль в 40 000 долларов, или будет полностью потеряна. Соответствующая ожидаемая прибыль равна 40 000 х 0.5 - 20000 х 0.5 = 10000 долларов. Хотя здесь ожидается прибыль в виде чистого дохода, разные люди могут по-разному интерпретировать полученный результат. Инвестор, который идет на риск, может сделать инвестицию, чтобы с вероятностью 50 % получить прибыль в 40 000 долларов. Наоборот, осторожный инвестор может не выразить желания рисковать потерей 20 000 долларов. С этой точки зрения очевидно, что разные индивидуумы проявляют разное отношение к риску, т.е. они проявляют разную полезность по отношению к риску.
Определение полезности является субъективным. Оно зависит от нашего отношения к риску. В этом разделе мы представляем систематизированную процедуру числовой оценки отношения к риску лица, принимающего решение. Конечным результатом является функция полезности, которая занимает место реальных денег.
В примере, приведенном выше, наилучший платеж равен $40 000, а наихудший – $20 000. Следовательно, мы устанавливаем произвольную, но логическую шкалу полезности U, изменяющуюся от 0 до 100, где 0 соответствует полезности -$ 20 000, а 100 – $40 000, т.е. U (-20000) = 0 и U(40000) = 100. Далее определяем полезность в точках между -$ 20 000 и $40000 для определения общего вида функции полезности.
Если отношение лица, принимающего решение, беспристрастно к риску, то результирующая функция полезности является прямой линией, соединяющей точки
(0, –$ 20 000) и (100, $ 40 000). В этом случае как реальные деньги, так и их полезность дают совпадающие решения. В более реальных ситуациях функция полезности может принимать другой вид, отражающий отношение к риску лица, принимающего решение. Рис. 14.5 иллюстрирует вид функции полезности для трех индивидуумов X, Y и Z. Индивидуум X не расположен к риску (осторожен), так как проявляет большую чувствительность к потере, чем к прибыли. Индивидуум Z – противоположность в этом отношении индивиду X; он настроен на риск. Это следует из того, что для индивидуума X при изменении в 10 000 долларов вправо и влево от точки, соответствующей 0 долларов, увеличение прибыли изменяет полезность на величину ab, которая меньше изменения полезности be, обусловленной потерями такой же величины, т.е. ab < be. В то же время такие же изменения в ±10 000 долларов, относящиеся к индивидууму Z, обнаруживают противоположное поведение; здесь de > ef. Далее, индивидуум Y является нейтральным к риску, так как упомянутые изменения порождают одинаковые изменения полезности. В общем случае индивидуум может быть как не расположен к риску, так и настроен на риск, в зависимости от суммы риска. В этом случае соответствующая кривая полезности будет иметь вид удлиненной буквы S.
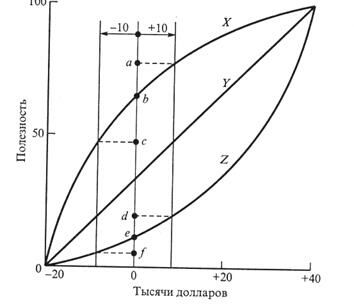
рис. 14.5
Кривые полезности, аналогичные изображенным на рис. 14.5, определены с помощью количественного показателя, характеризующего отношение к риску лица, принимающего решение, для различных значений уровня реальных денег в пределах установленного интервала. Так рассмотренном примере установленным интервалом является (– $ 20 000,
$ 40 000), соответствующая полезность изменяется в интервале (0, 100). Необходимо определить полезность, соответствующую таким промежуточным значениям, например, как – $10 000, $0, $10 000, $20 000 или $30 000. Соответствующая процедура построения функции полезности начинается с того, что организовывается лотерея для определения суммы реальных денег х, для которой ожидаемое значение полезности будет вычислено по следующей формуле.
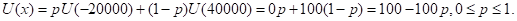
Для определения значения U(x) просят лицо, принимающее решение, сообщить свое предпочтение между гарантированной наличной суммой х и возможностью сыграть в лотерею, в которой с вероятностью р реализуется проигрыш в сумме $20000 и с вероятностью 1 – р имеет место выигрыш в $ 40 000. При этом под предпочтением понимается выбор значения "нейтральной" вероятности р, при котором с точки зрения лица, принимающего решение, возможности сыграть в лотерею и получить гарантированную сумму х являются одинаково привлекательными. Например, если х = $ 20 000, лицо, принимающее решение, может заявить, что гарантированные 20 000 долларов наличными и лотерея одинаково привлекательны при р = 0.8. В этом случае вычисляется полезность для х = $20 000 по следующей формуле.
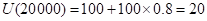
Эта процедура продолжается до тех пор, пока не будет получено достаточное количество точек (х, U(x)) для определения формы функции полезности. Затем можно определить искомую функцию полезности путем регрессионного анализа или просто линейной интерполяции между полученными точками.
Хотя здесь применяется количественная процедура для определения функции полезности, сам подход далек от того, чтобы быть научно обоснованным. То, что процедура полностью определяется мнением лица, принимающего решение, порождает сомнения относительно надежности описанного процесса. Процедура, в частности, неявно предполагает, что лицо, принимающее решение, является рационально мыслящим – требование, которое не всегда может быть согласовано с вариациями в поведении и настроении, что является типичным для человеческой личности. В этом отношении лицо, принимающее решение, должно придерживаться концепции полезности в широком смысле, в соответствии с которой денежные величины не должны быть единственным решающим фактором в теории принятия решений.
Упражнения 3.3,d
1. Допустим, вы – студент университета штата Арканзас и имеете сильное желание присутствовать на следующем баскетбольном матче. Проблема в том, что входной билет стоит 10 долларов, а у вас есть лишь 5 долларов. Вы можете рискнуть 5 долларами в игре в покер с шансами 50 на 50 удвоить свою сумму или совсем ее проиграть.
a) Будете ли вы, исходя из реальной стоимости денег, искушать судьбу, играя в покер?
b) Учитывая ваше сильное желание присутствовать на матче, переведите наличные деньги в функцию полезности.
с) Основываясь на функции полезности, которую вы построили, примете ли вы участие в игре в покер?
2. Семья переехала в местность, где возможны землетрясения, и собирается построить дом. Решается вопрос, стоит ли строить дом в соответствии с высокими стандартами, рассчитанными на сейсмическую зону. Строительство дома в соответствии с такими стандартами обойдется в 850 000 долларов, а без их учета – в 350 000 долларов. В случае землетрясения (его вероятность равна 0.001) восстановление дома, построенного без соответствующих стандартов, обойдется в 900 000 долларов. Примените в этой ситуации рассмотренную выше процедуру использования лотереи, предполагая, что шкала полезности изменяется от 0 до 100.
3. Инвестиция в 10 000 долларов в предприятие с высоким уровнем риска имеет шанс 50 на 50 увеличить эту сумму до 14 000 долларов на протяжении следующего года либо уменьшить ее до 8 000 долларов. Это значит, что чистый доход составит либо 4000 долларов, либо – 2000 долларов.
a) Принимая позицию нейтрального к риску инвестора и шкалу полезности от 0 до 100, определите полезность 0 долларов чистого дохода и соответствующую "нейтральную" вероятность.
b) Пусть два инвестора А и В определили следующие "нейтральные" вероятности.
| Чистая прибыль ($) | Вероятность | |
| Инвестор А | Инвестор В | |
| – 2000 | 1.00 | 1.00 |
| – 1000 | 0.30 | 0.90 |
| 0 | 0.20 | 0.80 |
| 1000 | 0.15 | 0.70 |
| 2000 | 0.10 | 0.50 |
| 3000 | 0.05 | 0.40 |
| 4000 | 0.00 | 0.00 |
Нарисуйте графики функций полезности для инвесторов А и В и охарактеризуйте их отношение к риску.
c) Пусть инвестор А имеет возможность сделать инвестицию в одно из двух рискованных предприятий: I или П. Инвестиция в предприятие I может принести прибыль в сумме 3000 долларов с вероятностью 0.4 или убыток в 1000 долларов с вероятностью 0.6. Инвестиция в предприятие II может принести прибыль в 2000 долларов с вероятностью 0.6 или вовсе не принести прибыли с вероятностью 0.4. Используя функцию полезности инвестора А, построенную в предыдущем пункте, и критерий ожидаемой полезности, определите предприятие, которое следует выбрать инвестору А. Каково ожидаемое денежное значение, соответствующее выбранному предприятию (используйте линейную интерполяцию функции полезности)?
d) Повторите упражнение предыдущего пункта для инвестора В.
3.4. Принятие решений в условиях неопределенности
Принятие решений в условиях неопределенности, как и в условиях риска, требует определения альтернативных действий, которым соответствуют платежи, зависящие от (случайных) состояний природы. Матрицу платежей в задаче принятия решений с m возможными действиями и n состояниями природы можно представить следующим образом.
| s1 | s2 | … | sn | |
| a1 | v(a1, s1) | v(a1, s2) | … | v(a1, sn) |
| a2 | v(a2, s1) | v(a2, s2) | … | v(a2, sn) |
| . | . | . | . | . |
| . | . | . | . | . |
| am | v(am, s1) | v(am, s2) | … | v(am, sn) |
Элемент ai представляет i-е возможное решение, а элемент sj – j-е состояние природы. Плата (или доход), связанная с решением аi, и состоянием sj, равна v(ai sj).
Отличие между принятием решений в условиях риска и неопределенности состоит в том, что в условиях неопределенности вероятностное распределение, соответствующее состояниям sj, j = 1, 2, ..., п, либо неизвестно, либо не может быть определено. Этот недостаток информации обусловил развитие следующих критериев для анализа ситуации, связанной с принятием решений.
1. Критерий Лапласа.
2. Минимаксный критерий.
3. Критерий Сэвиджа.
4. Критерий Гурвица.
Эти критерии отличаются по степени консерватизма, который проявляет индивидуум, принимающий решение, перед лицом неопределенности.
Критерий Лапласа опирается на принцип недостаточного основания1, который гласит, что поскольку распределение вероятностей состояний P(sj) неизвестно, нет причин считать их различными. Следовательно, используется оптимистическое предположение, что вероятности всех состояний природы равны между собой, т.е. . Если при этом v(ah sj) представляет получаемую прибыль, то наилучшим решением является то, которое обеспечивает
. Если при этом v(ah sj) представляет получаемую прибыль, то наилучшим решением является то, которое обеспечивает
 .
.
Если величина v(ai, sj) представляет расходы лица, принимающего решение, то оператор "max" заменяется на "min".
Максиминный (минимаксный) критерий основан на консервативном осторожном поведении лица, принимающего решение, и сводится к выбору наилучшей альтернативы из наихудших. Если величина v(ai, sj) представляет получаемую прибыль, то в соответствии с максиминнъш критерием в качестве оптимального выбирается решение, обеспечивающее
 .
.
Если величина v(ai, sj) представляет потери, используется минимаксный критерий, который определяется следующим соотношением.
 .
.
Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем замены матрицы платежей (выигрышей или проигрышей) v(ai, sj) матрицей потерь r(ai, sj), которая определяется следующим образом.
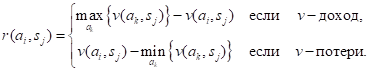
Чтобы показать, как критерий Сэвиджа "смягчает" минимаксный (максиминный) критерий, рассмотрим следующую матрицу платежей v(ai, sj):
| s1 | s2 | Максимум строк | ||
| a1 | $ 11 000 | $ 90 | $ 11 000 | |
| a2 | $ 10 000 | $ 10 000 | $ 10 000 | ß Минимакс |
Применение минимаксного критерия приводит к тому, что решение а2 с фиксированными потерями в 10000 долларов является предпочтительным. Однако можно выбрать а1, так как в этом случае имеется возможность потерять лишь 90 долларов, если реализуется состояние s2.
Посмотрим, какой результат получится, если в минимаксном критерии вместо матрицы платежей v(ai, sj) используем матрицу потерь r(ai, sj).
| s1 | s2 | Максимум строк | ||
| a1 | $ 1 000 | $ 0 | $ 1 000 | ß Минимакс |
| a2 | $ 0 | $ 9 910 | $ 9 910 |
Как видим, минимаксный критерий, применяемый к матрице потерь, приводит к выбору решения а1 в качестве предпочтительного.
Рассмотрим теперь критерий Гурвица. Этот критерий охватывает ряд различных подходов к принятию решений – от наиболее оптимистичного до наиболее пессимистичного (консервативного). Пусть 0 ≤ α ≤ 1 и величины v(ah sj) представляют доходы. Тогда решению, выбранному по критерию Гурвица, соответствует
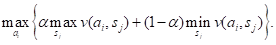
Параметр α – показатель оптимизма. Если α = 0, критерий Гурвица становится консервативным, так как его применение эквивалентно применению обычного минимаксного критерия. Если а = 1, критерий Гурвица становится слишком оптимистичным, ибо рассчитывает на наилучшие из наилучших условий. Мы можем конкретизировать степень оптимизма (или пессимизма) надлежащим выбором величины α из интервала [0, 1]. При отсутствии ярко выраженной склонности к оптимизму или пессимизму выбор α =0.5 представляется наиболее разумным.
Если величины v(ai, sj) представляют потери, то критерий принимает следующий вид:
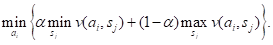
Пример 3.4-1
Национальная школа выживания подбирает место для строительства летнего лагеря в центре Аляски, в целях тренировки людей на выживание в условиях дикой природы. Школа считает, что число участников сбора может быть 200, 250, 300 или 350 человек. Стоимость летнего лагеря будет минимальной, поскольку он строится для удовлетворения только точно определенных небольших потребностей. Отклонения в сторону уменьшения или увеличения относительно идеальных уровней потребностей влекут за собой дополнительные затраты, обусловленные строительством избыточных (неиспользуемых) мощностей или потерей возможности получить прибыль в случае, когда некоторые потребности не удовлетворяются. Пусть переменные а1 – а4 представляют возможные размеры лагеря (на 200, 250, 300 или 350 человек), а переменные s1 – s4 — соответствующее число участников сбора. Следующая таблица содержит матрицу стоимостей (в тысячах долларов), относящуюся к описанной ситуации.
| s1 | s2 | s3 | s4 | |
| a1 | 5 | 10 | 18 | 25 |
| a2 | 8 | 7 | 12 | 23 |
| a3 | 21 | 18 | 12 | 21 |
| a4 | 30 | 22 | 19 | 15 |
Описанная ситуация анализируется с точки зрения четырех рассмотренных выше критериев.
Критерий Лапласа. При заданных вероятностях P{sj} = 1/4, j = 1, 2, 3,4, ожидаемые значения затрат для различных возможных решений вычисляются следующим образом.
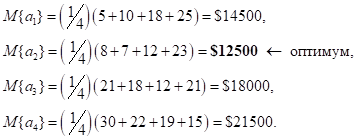
Минимаксный критерий. Этот критерий использует исходную матрицу стоимостей.
| s1 | s2 | s3 | s4 | Максимум строк | |
| a1 | 5 | 10 | 18 | 25 | 25 |
| a2 | 8 | 7 | 12 | 23 | 23 |
| a3 | 21 | 18 | 12 | 21 | 21 ← минимакс |
| a4 | 30 | 22 | 19 | 15 | 30 |
Критерий Сэвиджа. Матрица потерь определяется посредством вычитания чисел 5, 7, 12 и 15 из элементов столбцов от первого до четвертого соответственно. Следовательно,
| s1 | s2 | s3 | s4 | Максимум строк | |
| a1 | 0 | 3 | 6 | 10 | 10 |
| a2 | 3 | 0 | 0 | 8 | 8← минимакс |
| a3 | 16 | 11 | 0 | 6 | 16 |
| a4 | 25 | 15 | 7 | 0 | 25 |
Критерий Грвица. результаты вычислений содержатся в следующей таблице.
| Альтернатива | Минимум строк | Максимум строк | α (Минимум строки) + (1– α) (Максимум строки |
| a1 | 5 | 25 | 25-20α |
| a2 | 7 | 23 | 23-16α |
| a3 | 12 | 21 | 21-9α |
| a4 | 15 | 30 | 30-15α |
Используя подходящее значение для α, можно определить оптимальную альтернативу. Например, при α =0.5 оптимальными являются либо альтернатива а1 либо а2, тогда как при α = 0.25 оптимальным является решение а3.
Упражнения 3.4,а
1. Хенк – прилежный студент, который обычно получает хорошие отметки благодаря, тому, что имеет возможность повторить материал в ночь перед экзаменом. Перед завтрашним экзаменом Хенк столкнулся с небольшой проблемой. Его сокурсники организовали на всю ночь вечеринку, в которой он не хочет участвовать. Хенк имеет три альтернативы:
a1 — участвовать в вечеринке всю ночь,
а2 — половину ночи участвовать в вечеринке, а половину — учиться,
a3 — учиться всю ночь.
Профессор, принимающий завтрашний экзамен, непредсказуем в том смысле, что экзамен может быть легким (s1), средним (s2) или трудным (s3). В зависимости от сложности экзамена и времени, затраченного Хенком на повторение, можно ожидать следующие экзаменационные баллы.
| s1 | s2 | s3 | |
| a1 | 85 | 60 | 40 |
| a2 | 92 | 85 | 81 |
| a3 | 100 | 88 | 82 |
а) Порекомендуйте Хенку, какой выбор он должен сделать (основываясь на каждом из четырех критериев принятия решений в условиях неопределенности).
b) Предположим, что Хенк более заинтересован в оценке (в буквенном выражении), которую он получит на экзамене. Буквенным оценкам от A до D, означающим сдачу экзамена, соответствует 90, 80, 70 и 60 баллов. Иначе при числе баллов ниже 60 студент получает оценку F, которая свидетельствует о том, что экзамен не сдан. Изменит ли такое отношение к оценкам выбор Хенка?
2. В приближении посевного сезона фермер Мак-Кой имеет четыре альтернативы:
а1 — выращивать кукурузу,
а2 — выращивать пшеницу,
а3 — выращивать соевые бобы,
a4 — использовать землю под пастбища.
Платежи, связанные с указанными возможностями, зависят от количества осадков, которые условно можно разделить на четыре категории:
s1 — сильные осадки,
s2 — умеренные осадки,
s3 — незначительные осадки,
s4 — засушливый сезон.
Платежная матрица ( в тысячах долларов) оценивается следующим образом.
| s1 | s2 | s3 | s4 | |
| a1 | –20 | 60 | 30 | –5 |
| a2 | 40 | 50 | 35 | 0 |
| a3 | –50 | 100 | 45 | –10 |
| a4 | 12 | 15 | 15 | 10 |
Что должен посеять Мак-Кой?
3. Один из N станков должен быть выбран для изготовления Q единиц определенней продукции. Минимальная и максимальная потребность в продукции равна Q* и Q** соответственно. Производственные затраты TCi, на изготовление Q единиц продукции на станке i включают фиксированные затраты Ki и удельные затраты ci на производство единицы продукции и выражаются формулой Tсi = Ki + ciQ.
a) Решите задачу с помощью каждого из четырех критериев принятия решений в условиях неопределенности.
b) Решите задачу при следующих данных, предполагая, что 1000 ≤ Q ≤ 4000.
| Станок i | Ki ($) | ci ($) |
| 1 | 100 | 5 |
| 2 | 40 | 12 |
| 3 | 150 | 3 |
| 4 | 90 | 8 |
3.5. Введение в теорию игр
В практической деятельности весьма часто приходится рассматривать явления и ситуации, в которых участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными, или просто конфликтами.
Типичный конфликт характеризуется тремя основными составляющими:
заинтересованными сторонами,
возможными действиями этих сторон,
интересами сторон.
Конфликтная ситуация, взятая из реальной жизни, как правило, довольно сложна. К тому же ее изучение затруднено наличием многих разных обстоятельств, часть из которых не оказывает сколь-либо существенного влияния ни на развитие конфликта, ни на его исход. Поэтому для того, чтобы анализ конфликтной ситуации оказался возможным, необходимо отвлечение от этих второстепенных факторов, при удачном стечении обстоятельств позволяющее построить упрощенную формализованную модель конфликта, которую и принято называть игрой. От реальной конфликтной ситуации игра отличается еще и тем, что ведется по вполне определенным правилам.
Необходимость изучения и анализа конфликтов, представляемых в виде упрощенных математических моделей (игр), вызвала к жизни специальный математический аппарат — теорию игр.
Опишем некоторые основные понятия, используемые в этой теории.
Заинтересованные стороны называются игроками. Любое возможное для игрока действие (в рамках заданных правил игры) называется его стратегией. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией. Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней.
В этих условиях протекание конфликта состоит в выборе каждым игроком своей стратегии и в получении им в сложившейся ситуации выигрыша из некоторого источника. На этом пути создается теория игр с выигрышами.
Однако оценка игроком ситуации путем указания его выигрыша, вообще говоря, не всегда возможна практически и даже не всегда имеет смысл. В подобных случаях иногда удается вместо прямых численных оценок ситуаций указывать на их сравнительную предпочтительность для отдельных игроков. На этом пути создается теория игр с предпочтениями, включающая в себя как частный случай и теорию игр с выигрышами. В дальнейшем мы ограничимся рассмотрением только игр с выигрышами.
Изучение игр можно проводить с различных точек зрения. Мы будем стремиться к
– выработке принципов оптимальности, то есть того, какое поведение игроков следует считать оптимальным (разумным, целесообразным),
– выяснению реализуемости этих принципов, то есть установлению существования оптимальных в выработанном смысле ситуаций, и
– отысканию этих реализаций.
Одной из плодотворных форм реализации представлений об оптимальности можно считать понятие равновесия, при котором складывается такая (равновесная) ситуация, в нарушении которой не заинтересован ни один из игроков.
Именно ситуации равновесия могут быть предметом устойчивых договоров между игроками (ни у одного из игроков не будет мотивов к нарушению договора). Кроме того, ситуации равновесия являются выгодными для каждого игрока: в равновесной ситуации каждый игрок получает наибольший выигрыш (разумеется, в той мере, в какой это от него зависит).
Если в игре ситуации равновесия (в пределах отпущенных возможностей) нет, то, оставаясь в условиях стратегий, имеющихся у игроков, мы сталкиваемся с неразрешимой задачей. При возникновении подобных случаев естественно ставить вопрос о таком расширении первоначального понятия стратегии, чтобы среди ситуаций, составленных из новых, обобщенных стратегий, заведомо нашлись бы равновесные. Если такие обобщенные стратегии существуют, то обычно они представляются некоторыми комбинациями исходных стратегий (при этом, естественно, предполагается, что игра повторяется многократно). Для того, чтобы отличать прежние стратегии от новых, первые называют чистыми, а вторые — смешанными стратегиями.
Весьма плодотворным является представление смешанной стратегии как случайного выбора игроками их чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша. Игра, преобразованная таким образом, обычно называется смешанным расширением исходной игры.
Проиллюстрируем сказанное на примере одного из самых простых, но одновременно и наиболее изученных классов игр, на так называемых матричных играх. Исследование матричных игр интересно еще и потому, что к ним могут быть приближенно сведены многие игры более общего вида.
Затем мы кратко остановимся на вопросе классификации игр и рассмотрим еще два вида игр — позиционные игры и биматричные игры.
Часть I МАТРИЧНЫЕ ИГРЫ... 59
1. Равновесная ситуация. 60
2. Смешанные стратегии. 65
Основные определения. 65
Основная теорема матричных игр. 68
Основные свойства оптимальных смешанных стратегий. 68
3. Методы решения матричных игр. 69
Итерационный метод решения матричных игр. 77
Сведение матричной игры к задаче линейного программирования. 79
4. Примеры задач, сводимых к матричным играм.. 81
Несколько слов в заключение. 84
6. О классификации игр. 85
Часть II ПОЗИЦИОННЫЕ ИГРЫ... 86
1. Структура позиционной игры.. 86
2. Нормализация позиционной игры.. 88
3. Позиционные игры с полной информацией. 97
Несколько слов в заключение. 100
3.6 Принятие решений и теория игр. Примеры. 101
3.6.1. Оптимальное решение игры двух лиц с нулевой суммой. 102
Упражнения 3.6,а. 103
3.6.2. Решение матричных игр в смешанных стратегиях. 105
Упражнения 3.6,b. 107
Упражнений 3.6,с. 110
Бесплатная лекция: "7 Изучение социальной истории" также доступна.
3.7. Заключение. 111
Литература. 112
Комплексные задачи. 112
*Это не значит, что в условии неопределенности полностью отсутствует информация о задаче. Речь идет о том, что имеющиеся данные трудно или невозможно классифицировать по степени значимости их для принятия решения и что для этих данных, рассматриваемых как реализации случайных величин или процессов, неизвестна или не может быть определена их функция распределения или другие статистические характеристики.
[1] Пункт процента — это одна десятая процента.
1 Этот принцип впервые сформулирован Я. Бернулли.



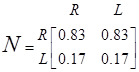
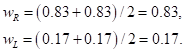
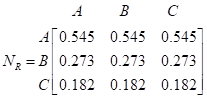
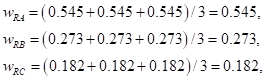
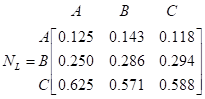
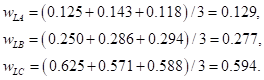
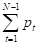
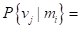
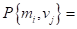
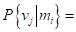
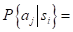
 с рекламной кампанией
с рекламной кампанией )
)

















