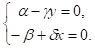Динамические модели

Глава I

Динамические модели

Модель — это представление объекта, системы или идеи в некоторой форме, отличной от самой целостности.

Р.Шеннон

1.1. Коротко о типах моделей

Не ставя перед собой задачи дать сколько-нибудь полную классификацию существующих моделей, коротко опишем некоторые их типы.

1.1.1. Физические модели

Так называют увеличенное или уменьшенное описание объекта или системы. Отличительная характеристика физической модели состоит в том, что в некотором смысле она выглядит как моделируемая целостность.

Наиболее известным примером физической модели является копия конструируемого самолета, выполненная с полным соблюдением пропорций, скажем 1:50. На одном из этапов разработки самолета новой конструкции возникает необходимость проверить его основные аэродинамические параметры. С этой целью подготовленную копию продувают в специальной (аэродинамической) трубе, а полученные показания затем тщательно исследуют. Выгодность такого подхода совершенно очевидна. И потому все ведущие самолетостроительные компании используют физические модели подобного рода при разработке каждого нового летательного аппарата.

Рекомендуемые материалы

Часто в аэродинамическую трубу помещают уменьшенные копии многоэтажных зданий, имитируя при этом розу ветров, характерную для той местности, где предполагается их строительство. Пользуются физическими моделями и в кораблестроении.

1.1.2Аналоговые модели

Так называют модели, представляющие исследуемый объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой.

Приведем два достаточно характерных примера.

Пример 1. График, иллюстрирующий соотношения между затраченными усилиями и результатами, является аналоговой моде­лью. График на рис. 1 показывает, как количество времени, отведенное студентом на подготовку к экзамену, влияет на его результат.

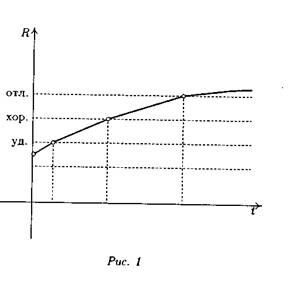
Пример 2. Предположим, что нужно найти наиболее экономичный способ для регулярных известных поставок товаров в три города, построив для этого только один склад. Основное требование: место для склада должно быть таким, чтобы полные транспортные расходы были наименьшими (считается, что стоимость каждой перевозки равна произведению расстояния от склада до пункта назначения на общий вес перевозимых товаров и измеряется в тонно-километрах).

Наклеим карту местности на лист фанеры. Затем в месте нахождения каждого города пропилим сквозные отверстия, пропустим через них нити и привяжем к ним грузики, пропорциональные запросам товаров в этот город (рис. 2). Свяжем свободные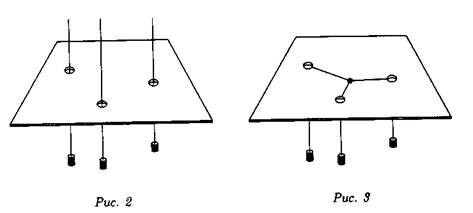

Концы нитей  в состояние равновесия. То место на листе фанеры, которое при этом займет узел, и будет соответствовать оптимальному расположению склада (рис. 3).

Замечание. Стоимость дорог, которые придется построить заново, мы для простоты рассуждений в расчет не принимаем.

1.1.3 Математические модели

Так называют модели, использующие для описания свойств и характеристик объекта или события математические символы и методы.

Если некоторую проблему удается перенести на язык формул, то она сильно упрощается. Математический подход прост еще и потому, что он подчиняется вполне определенным жестким правилам, которые нельзя отменить указом или иным способом. Сложность нашей жизни как раз и состоит в том, что многое, что в ней случается, нередко свободно от пут условностей.

Математика имеет дело с упрощенным описанием явлений. По существу, любая формула (или совокупность формул) представляет собой определенный этап в построении математической модели. Опыт показывает, что построить модель (написать уравнение) довольно легко. Трудно в этой модельной и, следовательно, упрощенной форме суметь передать суть изучаемого явления.

Для нахождения приемлемого или оптимального решения задачи полезно знать, в чем она состоит. Как ни просто и прозрачно данное утверждение, чересчур многие < ... > игнорируют очевидное (Р. Шеннон).

В предыдущих главах мы рассмотрели достаточное число разнообразных математических моделей, детерминированных, стохастических и игровых. В этой главе мы приведем примеры динамических моделей, на основании которых можно делать прогнозы на будущее и по-новому заглядывать в прошлое.

Итак, мы рассматриваем модели, в которые входят изменяющиеся во времени величины, уделяя основное внимание простейшим из них. Дело в том, что сами модельные уравнения (модели) строятся на основе простых и зачастую почти очевидных соображений. Именно анализ предлагаемых уравнений позволяет как-то оценить степень их адекватности описываемым ими обстоятельствам.

1.2. Модель народонаселения

Интересно, что построить математическую модель часто совсем нетрудно. Нередко для этого используются самые простые и легко объяснимые предположения.

Опишем, как это можно сделать, на одном почти реальном примере.

Представим себе следующую картину. Середина XVIII в. Центральная Европа. Приход в глубинке. Церковь. Прихожане — жители окрестных деревень. Приходский священник замечает, что храм стал тесноват для богослужений: возросло число прихожан. Священник размышляет: если число прихожан будет увеличиваться и в будущем, то придется строить новую церковь, для чего понадобятся средства, и немалые.

Священник понимает, что срок, за который должен быть построен храм, и его размеры во многом зависят от того, как именно будет изменяться число окрестных жителей. И он решает попытаться рассчитать это.

Попробуем и мы изложить возможный ход его рассуждений, пользуясь современными обозначениями и языком.

Обозначим через х_п количество прихожан к концу n-го года. Их численность через год, т. е. к концу (n + 1)-го года, естественно обозначить через x_n+1. Тогда изменение численности за этот год можно описать разностью

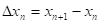
Оно происходит по двум естественным причинам — люди рождаются и умирают (для простоты будем считать, что вирус миграций эту  местность тогда еще не поразил). Определить число родившихся и число умерших за год по приходским книгам особого труда не составляет. Подсчитывая число родившихся и умерших в разные годы, священник решает сопоставить полученные числа

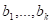
и

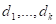
с общим числом прихожан за эти годы

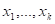
и замечает, что отношения

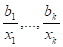
год от года отличаются весьма мало. То же касается и отношений

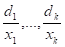
Для простоты расчетов будем считать эти отношения постоянными и обозначим их через  и  соответственно.

Тем самым, самым число родившихся в  году оказывается равным

,

число умерших

,

а изменение численности по естественным причинам составляет

+ -  .

В результате мы приходим к соотношению

= -  .

или подробнее:

=+ -  .

Положим

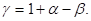
Тогда интересующая нас формула примет вид

=.

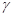
Модель построена.

Попробуем теперь разобраться с тем, что же получилось, т. е. проанализировать построенную модель. Возможны три случая:

1) (— рождается больше, чем умирает) и численность прихожан растет год от года,

2) ( — умирает столько же, сколько рождается и численность прихожан год от года остается неизменной,

3) ( — умирает больше, чем рождается) и численность прихожан неуклонно снижается.

Так как побудительным мотивом для построения модели было желание узнать, как быстро будет расти число прихожан, начнем с рассмотрения случая 1.

Случай 1. Итак, численность прихожан растет. Но как, насколько быстро?

Здесь самое время кратко вспомнить поучительную историю (печальную притчу) о безвестном изобретателе шахмат.

Говорят, что игра очень понравилась богатому и всесильному магарадже, который тут же решил наградить изобретателя и щедро предложил выбрать вознаграждение ему самому. Тот, как рассказывают, смахнув фигуры с шахматной доски, положил на 1-ю клетку одно пшеничное зернышко, на 2-ю — два зернышка, на 3-ю — четыре зернышка, на 4-ю — восемь зернышек (рис. 4) и предложил магарадже, чтобы он отдал распоряжение слугам выкладывать зерна пшеницы на другие клетки шахматной доски по предложенному закону, т. е. так:

1,2,4,8,16,...,2⁶³.

 

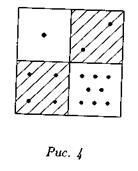
Магараджу эта простая просьба почти обидела, и он согласился выполнить ее далеко не сразу. Но изобретатель настаивал. Магараджа приказал. И слуги тут же кинулись исполнять это "легкое" задание. Нужно ли говорить, что выполнить распоряжение магараджи им не удалось. Дело в том, что общее количество зерен пшеницы на шахматной доске должно было быть равным

2⁶⁴-1,

что намного превышает выращиваемое сейчас во всем мире за год. Закончим притчу совсем коротко: магараджа оказался в непривычном для себя положении — он прилюдно дал обещание и не смог его выполнить. Виновного, впрочем, тут же и нашли. Возможно, именно поэтому история и не сохранила имени изобретателя шахмат.

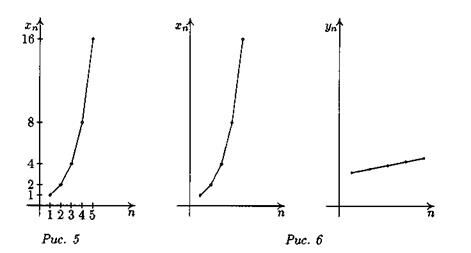
Попробуем, однако, изобразить на графике, как быстро растет число зерен в каждой следующей клетке, для большей наглядности соединяя соседние точки (рис. 5).

Правило, предложенное изобретателем шахмат,

,

является частным случаем формулы (1) при 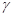 = 2 и, так же как и она, описывает закон, следуя которому мы получаем последователь­ность чисел, образующих геометрическую прогрессию.

При любом 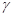 > 1 картинка, иллюстрирующая изменение х_n, имеет похожий вид – х_п будет расти экспоненциально.

В 1820 г. в Лондоне Т. Р. Мальтусом была опубликована работа “Principles of political economy considered with a view to their practical application” (в русском переводе – "Опыт о законе народонаселения..." Т. 1-2. СПб., 1868), в которой, в частности, говорилось о >м, что в силу биологических особенностей людей население имеет тенденцию размножаться по закону геометрической прогрессии:

х_п+1 = γx_n,        γ > 1,

то время как средства существования могут увеличиваться лишь > закону арифметической прогрессии:

y_п+1 = y_п + d,         d > 0.

Такое различие в скорости изменения величин, непосредственно вязанных с проблемами выживаемости популяции (рис. 6), не могло остаться незамеченным и вызвало довольно жесткую критику и сильно политизированную полемику в соответствующих кругах.

Попробуем извлечь из самого факта критики полезный для нас вод об адекватности построенной модели (1).

Разумеется, при попытке упрощенного описания ситуации некоторыми обстоятельствами приходится пренебрегать, считая их несущественными. Однако единого взгляда на то, что именно существенно, а что не очень, по-видимому, нет. Можно, например, не обращать внимания на то, что начался дождик. Но согласитесь, что одно дело пробежать под накрапывающим дождем сотню метров, и совсем другое – часовая прогулка под таким дождем без зонта.

Нечто аналогичное мы наблюдаем и здесь: при расчете на 3-4 года вперед формула (1) работает достаточно хорошо, но долгосрочный прогноз, основанный на ней, оказывается ошибочным.

Важный вывод. Предлагая построенную или выбранную вами модель, вы непременно должны указать пределы, в которых ею можно пользоваться, и предупредить о том, что нарушение этих ограничений может привести (и, скорее всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой ресурс.

Покупая блузку или рубашку, мы привыкли к наличию меток, на которых указаны максимально допустимая температура глажения, дозволенные виды стирки и т.п. Это, конечно, ни в коей мере не означает, что вам запрещается, взяв докрасна раскаленный утюг, пройтись им раз-другой по ткани. Такое вы сделать можете. Но вот захотите ли вы носить блузку или рубашку после такого глажения?

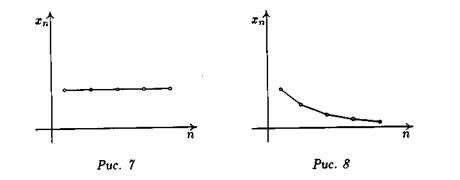
Случай 2. Численность населения не изменяется (рис. 7).

Случай 3. Население вымирает (рис. 8).

Мы умышленно весьма подробно остановились на описании модели народонаселения, во-первых, потому, что она является одной из первых моделей подобного рода, и, во-вторых, чтобы на ее примере показать, через какие основные этапы проходит решение задачи построения математической модели.

Замечание 1. Очень часто, описывая эту модель народонаселения, привлекают ее дифференциальный вариант:

x’=δx

(здесь х—x(t) — зависящая от времени численность популяции, х' — производная по времени, δ — постоянная величина).

Замечание 2. При больших значениях х конкурентная борьба за средства существования приводит к уменьшению δ, и эта жесткая модель должна быть заменена более мягкой моделью:

x’=δ(x)x,

в которой коэффициент δ зависит от численности населения. В простейшем случае эта зависимость описывается так:

δ(x)=a-bx,

где а и b — постоянные числа, а соответствующее уравнение принимает вид

x’=ax-bx².

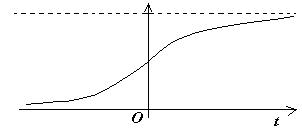
Рис. 9

И мы приходим к более сложной, так называемой логистической модели, которая описывает динамику популяции уже достаточно хорошо. Анализ логистической кривой (рис. 9) весьма поучителен, и его проведение может быть любопытно читателю.

Логистическая модель хорошо описывает и другие процессы, например эффективность рекламы.

1.3. Модель мобилизации

Под термином политическая, или социальная, мобилизация понимается вовлечение людей в партию или в число ее сторонников, в какое-либо общественное движение и т.п.

Вследствие того что текущий уровень мобилизации тесно связан с прошлым ее уровнем, а будущая мобилизация зависит от сегодняшних успехов пропагандистской кампании, ясно, что при построении соответствующей модели необходимо учитывать временной фактор. Иными словами, нужно понимать, что искомая модель должна быть динамической.

Постановка задачи

Отразить логику изменения уровня мобилизации в данном регионе аду двумя соседними моментами времени, скажем за месяц (за , неделю, день и т. п.).

Построение модели

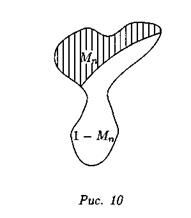
Примем за единицу ту часть населения, для которой мобилизация данного типа имеет смысл. Пусть М_п — доля мобилизованного населения в момент времени t_n = п. Тогда доля немобилизованного населения будет равна 1 — М_п (рис. 10).

За месяц уровень мобилизации может измениться по двум основным причинам:

1) часть населения удалось привлечь дополнительно; ясно, что эта величина тем больше, чем выше доля еще несагитированного населения на момент t_n = n, и поэтому можно считать ее равной

α(1 – M_n)

(здесь > 0 — коэффициент агитируемости, постоянный для данного региона);

2) часть населения убыла (по разным причинам); ясно, что это уменьшает долю сагитированного населения тем больше, чем выше была эта доля на момент t_n = п, и поэтому потери, связанные с выбытием, можно считать равными

β  M  _n

(здесь β > 0 — постоянный коэффициент выбытия).

Подчеркнем, что числовые параметры а и β отражают пропорциональное изменение интересов, взглядов и намерений соответствующих частей населения рассматриваемого региона.

Таким образом, изменение уровня мобилизации за единицу времени

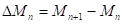
равно разности между долей населения, привлеченного дополни­тельно, и долей выбывшего сагитированного населения:

М_n+1 – М_n = α(1 - М_п) - βМ_п.

Это и есть уравнение процесса мобилизации. Модель мобилизации построена.

Последнее соотношение легко преобразуется к следующему виду:

                                   М_n+1 = α+γМ_п,                                                                                        (2)
где

γ=1-α-β.

Замечание. Вспомогательный параметр γ не может быть больше 1 вследствие того, что исходные параметры α и β положительны.

Полученное уравнение (2) называется линейным разностным уравнением с постоянными коэффициентами.

С уравнениями подобного рода читатель, несомненно, уже не раз сталкивался, правда, по большей части в простейших вариантах.

Один из них (при γ=1) описывает правило, по которому каждый член последовательности, начиная со второго, получается из предыдущего путем сложения с некоторым постоянным числом:

M_n+1 =α + М_n,

т. е. арифметрическую прогрессию.

Второй (при а=0) описывает правило, по которому каждый член последовательности, начиная со второго, получается из предыдуще­го путем умножения на некоторое постоянное число:

М_п+1 = γM_n

т. е. геометрическую прогрессию.

Предположим, что начальная доля привлеченного населения m₀ известна. Тогда уравнение (2) легко решается (для определенности считаем, что γ1). Имеем:

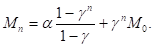
Применение модели

Попробуем проанализировать возможности этой (построенной на основании  простейших соображений) модели.

Начнем со случая <1.

Для этого перепишем последнее соотношение в виде

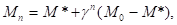
где через М* обозначена следующая величина:

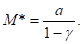
Замечание. Тот же результат получается, если в уравнении (2) положить

M_n+1 =М_n=М*.

В самом деле, тогда получим

M* =α + γМ*,

откуда

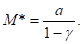
Найденная величина M* не зависит от начального значения М₀, выражается через исходные параметры α и β по формуле

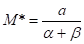
и, следовательно, подчинена условию

0<M*<1.

Для придания полученной формуле большей наглядности воспользуемся методом координат.

На рис. 11 показаны области возможных значений вспомогательного параметра 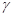 на рис. 12 — исходных параметров а и β, а на рис. 13-15 — соответствующие им наборы значений М_n при разных п, М₀ и М* (для удобства восприятия соседние точки (п, М_n) и (n+ 1, M_n+1) соединены прямолинейными отрезками).

Случай γ < – 1 проиллюстрирован на рис. 16.

Конечно, на этих рисунках представлена качественная картина. Но ничто не мешает взять вполне конкретные значения величин М₀, а и β и подробно рассчитать соответствующую ситуацию.

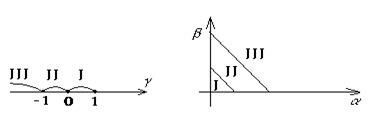
Рис.11                        Рис.12

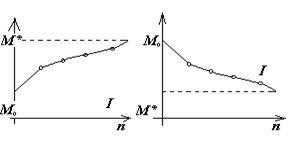
Рис.13                        Рис.14

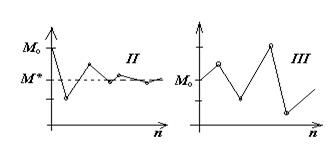
Рис. 15                       Рис. 16

Например, для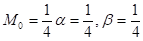

Имеем  (рис.17).

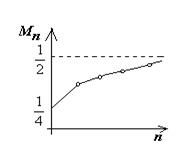
Рис.17

Интересно отметить, что построенная модель, несмотря на про­стоту подходов и рассуждений, довольно хорошо отражает реальные процессы. Так, предложенная модель мобилизации использовалась для изучении динамики числа голосов, поданных за демократиче­скую партию в Лейк Кантри (США) в 1920-1968 гг., и оказалось, что она достаточно хорошо описывает качественные характеристи­ки процесса мобилизации.

1.4. Модель гонки вооружений

Рассмотрим конфликтную ситуацию, в которой могут оказаться две соседние страны, для определенности названные странами X и Y.

Обозначим через x=-x(t) расходы на вооружение страны X и через y = y(t) расходы на вооружение страны Y в момент времени t £ 0.

Предположение 1

Страна Х вооружается, опасаясь потенциальной угрозы войны со стороны страны Y, которая в свою очередь, зная о росте затрат на вооружение страны X, также увеличивает свои расходы на вооружение. Каждая страна изменяет скорость роста (или сокращения) вооружений пропорционально уровню затрат другой. В простейшем случае это можно описать так:

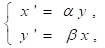
где а и β — положительные постоянные.

Однако написанные уравнения имеют очевидный недостаток – уровень вооружения ничем не лимитируется. Поэтому правые части этих уравнений нуждаются в естественной корректировке.

Предположение 2

Чем больше текущий уровень расходов страны на оборону, тем меньше скорость его роста. Это позволяет внести в предыдущую систему следующие изменения:

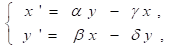
где a и β — положительные постоянные.

Предположение 3

Каждая страна наращивает вооружение, руководствуясь своими державными притязаниями и враждебностью к соседней стране, даже если эта страна не угрожает существованию данной. Обозначим соответствующие претензии через а и b (а и b – положительные постоянные). В случае если постоянные а и b отрицательны, их можно назвать коэффициентами доброй воли.

Основываясь на всех трех предположениях, в результате получаем следующую систему уравнений:

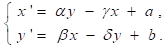
Модель гонки вооружений построена.

Решением полученной системы являются функции x(t) и y(t), определяемые для данных начальных условий х₀ ≥ 0 и у₀ ≥ 0 (начального состояния гонки вооружений).

Проанализируем полученную систему, предполагая, что уровни затрат обеих стран на вооружение не зависят от времени (являются стационарными). Это означает, что

x’=0, y’=0,

или по-иному:

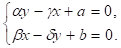
Рассмотрим конкретный пример.

Пример 3. Пусть система уравнений гонки вооружений имеет следующий вид:

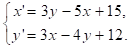
Если скорости изменения величин x и y равны нулю, то эти величины с необходимостью связаны условиями

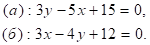
Каждое из этих уравнений описывает прямую на плоскости (x, y), и точка пересечения этих прямых

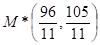
лежит в первой четверти (рис.18).

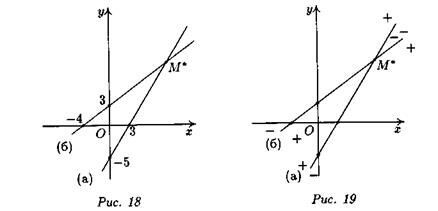
Прямая, заданная уравнением (а), разбивает плоскость, и начальная точка О (0,0) лежит в положительной полуплоскости. В рассматриваемом случае то же справедливо и для прямой, заданной уравнением (б) (рис. 19).

Тем самым первая четверть (а нас интересует только она, так как всегда х ≥ 0 и у≥0) разбивается на четыре области, которые удобно обозначить так

I – (+, +), II – (–, +), III – (–, –), IV – (+,–).

Пусть начальное состояние (х₀, y₀) находится в области I. Тогда выполнены неравенства

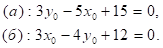
из которых следует, что скорости х' и у' в этой точке положительны и, значит, обе величины (х и у) должны возрастать (рис. 20).

Таким образом, с течением времени в области I решение приходит в точку равновесия.

Подобным же образом анализируя возможные расположения начального состояния в областях II, III и IV, получим в итоге, что стабильное состояние (баланс сил) достигается независимо от начальных уровней вооружения стран X и Y. Отличие состоит лишь в том, что если переход к стационарному состоянию из области I сопровождается одновременным увеличением уровней вооруженности,

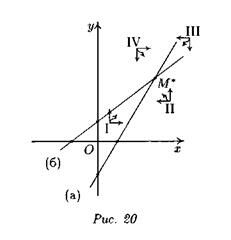
то из области III — их одновременным снижением; для областей II и IV иная ситуация – одна из сторон наращивает свое вооружение, в то время как другая разоружается.

Возможны и другие случаи (рис. 21)

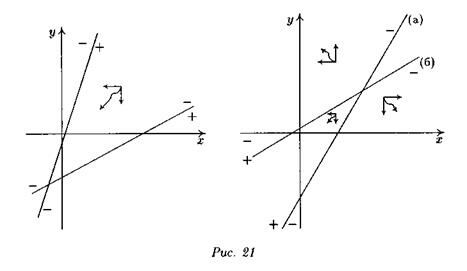
Интересно отметить, что возможности построенной модели проверялись на реальной ситуации – гонке вооружений перед первой мировой войной. Проведенные исследования показали, что, несмотря на свою простоту, эта модель достаточно достоверно описывает положение дел в Европе в 1909-1913 гг.

В завершение этого раздела процитируем высказывание Т. Саати об этой модели: "Модель представляется гораздо более убедительной, если вместо вооружений провести на ней изучение проблем угрозы, поскольку люди реагируют на абсолютный уровень враж­дебности, проявляемый по отношению к ним другими, и испытывают чувство тревоги в степени, пропорциональной уровню враждебности, которую они испытывают сами".

1.5. Модель хищник - жертва

Выше рассказывалось о беспрепятственном размножении популяции. Однако в реальных обстоятельствах популяция сосуществует с другими популяциями, находясь с ними в самых разных взаимо­отношениях.

Здесь мы коротко рассмотрим антагонистическую пару хищник – жертва (это может быть и пара рысь - заяц и пара божья коровка - тля) и попытаемся проследить, как может изменяться со временем численность обеих взаимодействующих сторон.

Популяция жертвы может существовать сама по себе, в то врем: как популяция хищника – только за счет жертвы.

Обозначим численность популяции жертвы через х, а численность популяции хищника через у.

В отсутствие хищника жертва размножается согласно уравнению.

x’=αx,                         a>0,

а хищник в отсутствие жертвы вымирает по закону

y’= – βy,                     β>0.

Хищник съедает тем больше жертвы, чем ее больше и чем более многочислен он сам. Поэтому при наличии хищника численное:

x’=ax – γxy,                γ>0.

Съеденное количество жертвы способствует размножению хищник что можно записать так

y’= – βy+ δxy,                        β>0.

Таким образом, мы получаем систему уравнений

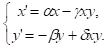
причем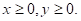

Модель хищник-жертва построена.

Как и в предыдущей модели, наибольший интерес для нас представляет точка равновесия (x*, y*), где x* и y* – отличное от нуля решение системы уравнений

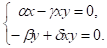
или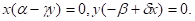

Эта система получается из условия стабильной численности обеих популяций x’=0, y’=0.

Координаты точки равновесия – она является точкой пересечения прямых

– легко вычисляются:                                                                              (рис.22).

Начало координат О(0,0) лежит в положительной полуплоскости относительно горизонтальной прямой, задаваемой уравнением (3), а относительно вертикальной прямой, задаваемой уравнением (4), — в отрицательной полуплоскости (рис. 23).

Тем самым первая четверть (а нас интересует только она, так как х > 0 и у > 0) разбивается на четыре области, которые удобно обозначить так:

I – (+, +), II – (–, +), III – (–, –), IV – (+,–).

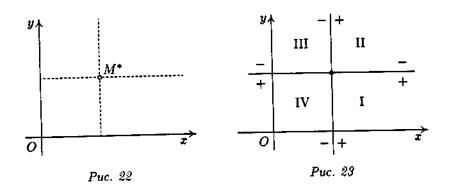
Пусть начальное состояние Q(x₀, у₀) находится в области IV. Тогда выполнены неравенства

     

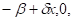
из которых следует, что скорости х' и у' в этой точке должны быть разных знаков,
х' > 0,       у' < 0,

и, значит, величина х должна возрастать, а величина у убывать. Подобным же образом анализируя поведение х и у в областях III и IV, получим в итоге картину, изображенную на рис. 24.

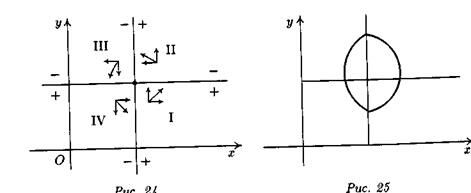
Тем самым начальное состояние Q приводит к периодическому колебанию численности как жертвы, так и хищника, так что прошествии какого-то времени система вновь возвращается в состояие Q (рис. 25).

Ещё посмотрите лекцию "План финансового оздоровления" по этой теме.

Как показывают наблюдения, несмотря на свою простоту, предложенная модель качественно верно отражает колебательный характер численности в системе хищник - жертва (рис. 26).

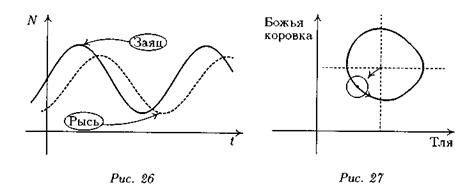
Реальные наблюдения. Вмешиваться в действия непонятных нам законов природы иногда довольно опасно — применение инсектицидов (если только они не уничтожают насекомых практически полностью) в конечном счете приводит к увеличению популяции тех насекомых, численность которых находится под контролем других насекомых-хищников.

Случайно попавшая в Америку тля поставила под угрозу все производство цитрусовых. Вскоре туда же был завезен ее естественный враг – божья коровка, которая немедленно принялась за дело и сильно сократила популяцию тли. Чтобы ускорить процесс уничтожения, фермеры применили ДДТ, но в результате количество тли увеличилось, что, глядя на рис. 27, нетрудно предугадать.

1.6. Заключение

Построение модели опирается на значительное упрощение изучаемой ситуации, и. следовательно, к получаемым на ее основе выводам нужно относиться достаточно осторожно – модель может не все. Вместе с тем даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирать их, управлять ими), мы получаем возможность подвергнуть исследуемое явление качественному анализу и сделать выводы общего характера.